Algorithms to Antenna: Modeling Polarization in Radar and Wireless Systems
In this blog, I describe polarization and explore ways you can analyze the polarized field as well as model the signal transmission between polarized antennas and targets.
From Maxwell’s equations, the electromagnetic (EM) field generated by an antenna is orthogonal to the propagation direction in the far field. The field can be decomposed into two orthogonal components. The most common representations of these components are either horizontal and vertical (H, V) sets or left and right circular (L, R) sets.
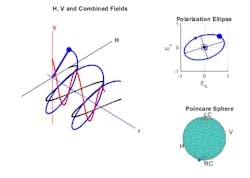
The simplest type of polarization is linear polarization, which happens when the two components are always in phase. Figure 1 shows the polarization for this case.
1. Shown is a visualization of the right-hand circular polarized field. The V component is represented as red, and the H component is represented as a black line in left plot.
From the plot in the top right of Fig. 1, you can see that the combined polarization is along the 45-deg. diagonal. This plot is often referred to as the polarization ellipse. It’s the projection of the combined field trace on the H-V plane.
A polarized field can also be represented by four elements, which are known as a Stokes vector. All four entries in the vector are real numbers, and all are measurable. Each set of Stokes vectors can be considered as a point on a sphere. The Poincaré sphere for the above field is shown in the bottom right portion of Fig. 1.
I encourage you to take a look at this Modeling and Analyzing Polarization example to see how a circular polarized field is represented.
Polarized Antennas
The polarization of an antenna is defined as the polarization of the field transmitted by the antenna. Some antennas, such as dipoles, have a structure that determines its polarization. A dipole antenna has a polarization that’s parallel to its orientation.
When two antennas form a transmit/receive pair, their polarization affects the received signal power. To collect a signal with the maximum power possible, the receive antenna's polarization should match that of the transmit antenna. I modeled this scenario, and the results are shown in Figure 2. Note there’s no loss due to polarization mismatch as both are vertically polarized, as shown in the plots on the left. If, instead, a horizontally polarized antenna is used to receive the signal, the two antennas are now orthogonal in polarization. As a result, no power will be delivered to the received antenna, as shown in the plot on the right side of Fig. 2.
2. The polarization effects when transmit and receive antennas have the same polarization are depicted on the left. The right side shows the effects when they have orthogonal polarization.
Using radar as an example, when an EM wave hits the target, the wave will be scattered, and some energy will be transferred between two orthogonal polarization components. The target scattering mechanism can be modeled by a 2-×-2 radar cross-section (RCS) matrix (also known as a scattering matrix); its diagonal terms specify how the target scatters the energy into the original H and V polarization component. The off-diagonal terms specify how the target scatters energy into the opposite polarization component.
Because any combination of polarizations is possible with transmit and receive antennas, you can look at the polarization signature for a target for different polarization configurations. The signature plots the received power under different polarizations as a function of the tilt angle and the ellipticity angle of the transmit polarization ellipse. This can also be considered a measure of the “effective RCS.”
Two widely used polarization signatures are co-polarization (co-pol) response and cross-polarization (cross-pol) response. Co-pol response uses the same polarization for both transmit and receive, while the cross-pol response uses the orthogonal polarization to receive.
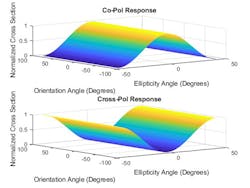
3. This figure reveals co-pol and cross-pol responses of a sphere.
To illustrate this, a sphere has an RCS matrix given by [1 0;0 1], meaning that the reflected polarization is the same as the incident polarization. The polarization signature for a sphere is shown in Figure 3.
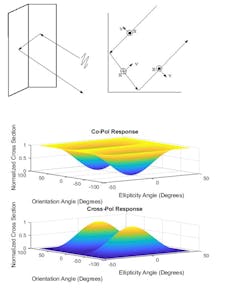
For a more complicated target shape such as a dihedral, the wave reflects twice, as shown on the top of Figure 4.
4. Shown are co-pol and cross-pol responses for a dihedral target shape.
The center of Fig. 4 illustrates how the polarization field changes along the two reflections. After the two reflections, the horizontal polarization component remains the same, while the vertical polarization component is reversed. The polarization signature appears in the bottom portion of Fig. 4.
With these modeling building blocks in place, I will show how polarization can be useful in a radar model.
Polarimetric Weather Radar
For the example, let’s look at a polarimetric Doppler weather radar based on the NEXRAD specifications. A polarimetric radar transmits RF pulses that have both horizontal and vertical orientations. After received pulses are synthesized, the radar spectral moment and polarimetric moment are estimated. The estimates are compared with NEXRAD ground truth, from which error statistics are evaluated.
The NEXRAD systems have antenna patterns with a beamwidth of about 1 degree, as shown in Figure 5. This antenna-array design is used in the model.
5. This is the antenna pattern of NEXRAD radar.
Weather targets are polarimetric and distributed in a plane. They can be represented by specifying a scattering matrix at discrete azimuth angles. Weather target reflectivity is defined as mean backscattering cross-section per unit volume. Based on weather-radar equations, weather targets can be considered as a collection of small targets within each resolution volume. Therefore, the overall reflectivity can be transformed to mean RCS and regarded as an equivalent scattering center. As a result, each element in the scattering matrix is the square root of RCS in relevant polarization. These can be brought into a model with the components I described in the first portion of the blog.
Within each resolution volume, correlation is included to ensure that the resulting I/Q data presents proper weather signal statistical properties. Using pulse pair processing, all radar moments are calculated from correlation estimates, including reflectivity, mean radial velocity, spectrum width, differential reflectivity, correlation coefficient, and differential phase.
The simulation results can be compared with the NEXRAD ground truth. Error statistics are expressed as the bias and standard deviation of the estimated radar moments compared with the NEXRAD Level II data (truth fields).
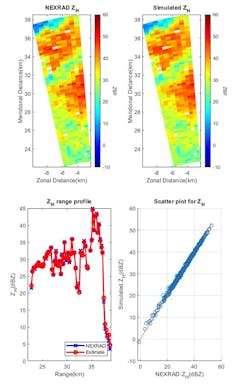
One measure, reflectivity (Z), is the zeroth moment of the Doppler spectrum and related to liquid water content or precipitation rate in the resolution volume. Figure 6 shows the comparisons of measured data from NEXRAD and the simulated results.
6. Reflectivity for measured (NEXRAD data) and simulated results are compared.
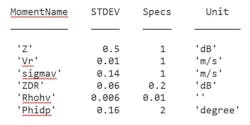
In the Simulating a Polarimetric Radar Return for Weather Observation example, other radar observations are compared with the results obtained through modeling and simulation. You can also see the quantitative comparison of the estimates with NEXRAD specifications as error statistics:
We can see that all the radar moment estimation can meet NEXRAD specifications, which indicates good data quality. Having simulation results that match observed data so closely opens the doors for additional exploration into algorithm design and system architectures.
To learn more about the topics covered in this blog, see the links below or email me at [email protected].
- Modeling and Analyzing Polarization (example): Learn basic concepts of polarization and how to analyze the polarized field and model the signal transmission between polarized antennas and targets.
- Simulating a Bistatic Polarimetric Radar (example): Learn how to simulate a polarimetric bistatic radar system to estimate the range and speed of targets.
- Simulating a Polarimetric Radar Return for Weather Observation (example): Simulate a polarimetric Doppler radar return that meets the requirements of weather observations.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
About the Author
Rick Gentile
Product Manager, Phased Array System Toolbox and Signal Processing Toolbox
Rick Gentile is the product manager for Phased Array System Toolbox and Signal Processing Toolbox at MathWorks. Prior to joining MathWorks, Rick was a radar systems engineer at MITRE and MIT Lincoln Laboratory, where he worked on the development of several large radar systems. Rick also was a DSP applications engineer at Analog Devices, where he led embedded processor and system level architecture definitions for high performance signal processing systems used in a wide range of applications.
He received a BS in electrical and computer engineering from the University of Massachusetts, Amherst, and an MS in electrical and computer engineering from Northeastern University, where his focus areas of study included microwave engineering, communications, and signal processing.