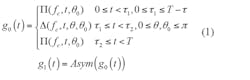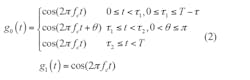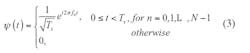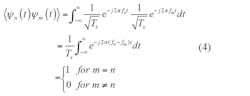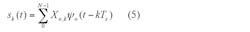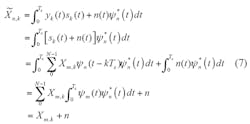Compressed UNB-OFDM Delivers High Data Rates

Proponents of UNB technologies have often questioned the need for wide continuous spectrum.^6-8 In theory, without sidebands, UNB communications channels can be closely spaced while still making it possible to receive demodulated UNB modulated signals. As will be shown, different UNB channels can be closely spaced while still enabling effective communications at high data rates. Also, a wide continuous spectrum is unnecessary, and the spread continuous spectrum can be compressed as narrow as possible—as much as Shannon’s limit defines, such as 1 Hz or less for UNB methods.

Traditional filtering techniques will not work with UNB modulation methods owing to the large group delay of those filters.^3,5 Filters with zero or negative group delay or similar mathematical methods realizing the same zero-group-delay principle are required to compress or filter modulated UNB signals. For example, a fractal transform can be used to compress the unnecessary sideband to achieve the goal of filtering UNB modulated signals.

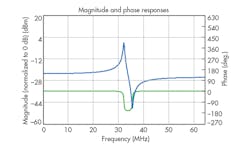
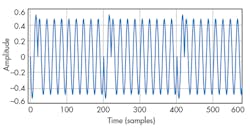
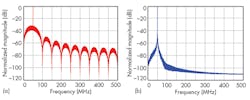
Figure 1 presents a filter with negative group delay.³ With such a filter, any UNB modulated information can be retained after filters, even though the filter’s 3-dB bandwidth is extremely narrow (for instance, 1 to 2 kHz). To demonstrate UNB modulation, Fig. 2 shows a recovered UNB-modulated signal passed through a filter with negative group delay, while Fig. 3a shows the frequency characteristics of the filter and Fig. 3b displays the signal’s power spectral density (PSD).

As can be seen, while there is no sideband for the UNB signal, the phase characteristics are not degraded. Some amplitude attenuation occurs with a zero-group-delay filter for UNB modulation, but the amplitude can be regained through amplification.¹

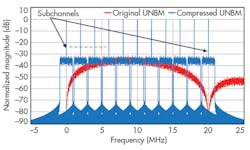
As these filter response plots show, the modulated signal sideband for UNB modulation is unnecessary and can be compressed to a large extent. This allows multiple UNB modulated signals to be placed closely together for multiple-signal or multiple-band communications with higher data rates compared to single-channel UNB communications schemes. Multifold data rates can be achieved through the use of closely spaced UNB modulated signals (Fig. 4).

In Fig. 4, the red trace represents the original UNB modulated signal. The continuous spectrum is very wide due to the use of asymmetrical modulation.⁶

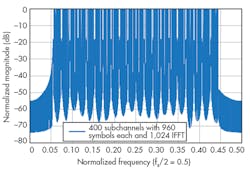
Once UNB-modulated signals have been compressed, multiple UNB signals can be placed within the same frequency band. As Fig. 4 shows, at least 10 compressed UNB signals with the same data rate can be placed within a limited bandwidth, improving the data rate by a factor of 10 compared to a single UNB signal in the same bandwidth.

For example, starting with a single signal data rate of 12 Mb/s,³ a data rate of 120 Mb/s can be achieved with 10 closely placed UNB-modulated signals within a common bandwidth. Orthogonal frequency division multiplexing (OFDM) is an efficient multichannel communications technique that can be applied to the use of multiple UNB-modulated signals to achieve an increase in data rate in this manner (Fig. 5).

The high spectral efficiency of OFDM has made high data rates possible in many communications systems and devices. With the ready availability of fast-Fourier-transform (FFT) technology in communications integrated circuits (ICs), OFDM has become practical and widespread in commercial systems. This is also why it has been possible to implement a compressed UNB-OFDM communications system.

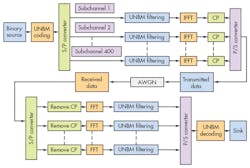
A multicarrier communications system divides available bandwidth into subchannels, each with its own data stream, and then multiplexes them prior to transmission. Each subchannel can be reserved for distinct data streams, or one data stream can be divided into N-data streams for N-subchannels.⁹Figure 5 shows a block diagram of a multicarrier system, where the block labeled ”Binary Source” features UNB modulation coding. A serial-to-parallel converter transforms coded UNB modulation data to parallel data streams, which correspond to the different subchannels.

Each subchannel is filtered, with its bandwidth compressed using negative-group-delay filters or other mathematical approaches (such as the use of fractal transforms). This results in OFDM using FFT techniques, with cyclic prefix (CP) appended to limit intersymbol interference (ISI). Following this, parallel modulated data is converted to a serial data stream for transmission, with an arbitrary white Gaussian noise (AWGN) channel used to transmit compressed UNB modulated OFDM signals.

At the receiver, received data is reshaped to parallel subdata streams and the CP is removed, with UNB filtering applied to enhance the modulation characteristics. All of the subchannels are reshaped to the original serial data to decode the UNB modulated signals and recovery the binary data. In this way, a system with a high-data-rate requirement can be divided into N lower-rate subchannels. The lower rates feature longer symbol durations than higher-rate signals and, with an added guard band, can help minimize intersymbol interference (ISI).

If the subchannels are narrow enough, the channel frequency response is approximately constant with respect to each subchannel. This makes equalization much less complicated than in a single-carrier system. While the subchannels can be chosen in any manner with respect to bandwidth, center frequency, and guard interval, a special case was considered in which subchannel parameters allow for increased bandwidth efficiency (near-Nyquist efficiency) and computationally efficient modulator and demodulator design.

The general wave function for UNB modulation can be written as Eq. 1⁶:

where Π(f, t, θ₀) can represent a variety of different digital signals, such as sine-wave or rectangular-wave signals, with τ = τ₂ – τ₁; Δ is the change or modulation to the Π(f, t, θ₀) wave in amplitude, phase, or frequency; θ is the modulation phase angle within the range [0 π]; θ₀ is the initial phase of the signal, which can have any value in the range [0 π]; Asym indicates asymmetric operation; and f_c is the carrier frequency of the modulated signal.

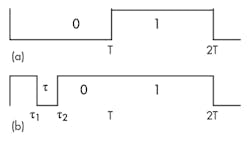
Additional parameters are T, which is the bit period, while τ is the duration of the modulation, with a value between 0 and T. Also, g₀(t) represents a digital “0” state, while g₁(t) is the digital “1” state. The parameter τ/T can be seen as the modulation duty cycle while also representing the degree of asymmetry for g₀(t). The basic principle is illustrated in Fig. 6.    

If Π(f_c, t, θ₀) = cos(2πf_ct), Δ(f_c, t, θ, θ₀) = cos(2πf_ct + θ), and g₀(t) = cos(2πf_ct), pulse-position phase reversal keying (3PRK) can be denoted by Eq. 2:

where the variables have been defined for Eq. 1, and where θ ≠ 0, g₀(t) and g₁(t) denote biphase modulation, and the modulation angle is defined by the range of [0, π]. If τ = T, the modulation is BPSK.

If W is the channel bandwidth and N is the number of subcarriers, then the subchannel bandwidth is described by Δf = W/N and the effective symbol rate is T_s = 1/Δf = N/W. The subcarrier frequencies are f_n = nΔf = n(W/N), where the subcarrier spacing is Δ = W/N for n = 0, 1…N – 1. The basic pulse waveform for UNB modulation can be defined by Eq. 3⁹:

which expresses a normalized rectangular pulse at frequency f_n. The inner product has the property described by Eq. 4:

The OFDM symbol is a linear combination of the subchannel symbols or pulses which can be considered as a set of orthogonal basis vectors. Thus, the OFDM symbol can be described by Eq. 5:

where k is the kth OFDM symbol; n is the nth subchannel; and X_n,k is the kth UNB symbol in the nth subchannel. The transmitted signal can then be described by Eq. 6:

Assuming an AWGN channel, the received signal for the kth OFDM symbol can be found by means of Eq. 7:

where n(t) is an additive Gaussian random process. To demodulate the nth OFDM symbol, the received signal is correlated with matched filter Ψ^*_n(t). Because the pulses are orthonormal, the correlation will be 0 for m = n and 1 for m = n.

Based on the theory so far presented, a computer simulation was carried out on the UNB system. The simulation was based on a frame with 400 subchannels, each with 960 symbols, and a 1,024-point FFT. For UNB modulation, coding rates from 1 to 10 were employed. Figure 7 offers a comparison of the power spectral densities (PSDs) for different bandwidths—one a Nyquist bandwidth, and the other a two-fold Nyquist bandwidth.

These two different-bandwidth signals were used during the simulation to calculate the BER and to verify that continuous spectrum is not necessary for effective use of UNB modulation for high-data-rate communications. Depending upon different scenarios, UNB-modulated signals can be placed close together, without sidebands to separate them. In contrast to the two different bandwidth signals of Fig. 7, Fig. 8 shows the PSD of an UNB-OFDM signal with all subchannels closely spaced.

Figure 9 presents the recovered time wave signals of the two corresponding different UNB-modulated signals of Fig. 6. The phase reversal is clear after being demodulated, which directly shows that the redundant sideband is not necessary, and can be compressed.

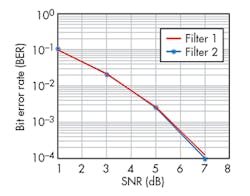
After 20 simulation runs, the average BER curves were plotted (Fig.10), with data from those simulations presented in Table 1. The curve with an asterisk marker corresponds to the BER for the Nyquist bandwidth, while the other curve is the BER plot of the UNB-modulated signal with twofold Nyquist bandwidth. As is apparent, the BER is not deteriorated by bandwidth compression, emphasizing that sidebands are not needed for separation of the multiple channels in an UNB-OFDM system and can be compressed.

For UNB modulation, the continuous spectrum spread is represented by T/τ. For RF modulation such as UNB modulation, the width of the continuous spectrum is 2T/τ. As has been shown, a wide continuous spectrum can be compressed. Using compressed UNB-OFDM, T/τ to 2T/τ different subchannels can be deployed in the same frequency band that is occupied by a single-carrier UNB continuous spectrum. This can improve the data rate by T/τ to 2T/τ compared to data rates provided by single uncompressed UNB modulated signals.

Table 2 offers a comparison between compressed UNB-OFDM and PPM UNB. Data rates can be improved by T/τ to 2T/τ times using compressed UNB-OFDM, while PPM-UNB only increases the data rate by log₂(T/τ) times. For a typical 500-MHz UWB frequency band, if compressed UNB-OFDM is deployed, a data rate of 500 Mb/s can be achieved. The spectral efficiency is significantly improved with UNBOFDM compared to conventional UWB communication methods, even when PPM technology is used. For a single user in an extreme case, for the full UWB frequency band, a data rate of about 7 Gb/s is possible with UNB modulation, making it an intriguing candidate for emerging 5G communications applications.

Acknowledgment

This work was supported by the National Natural Science Foundation of China (NSFC) under Grant No. 61001102.

Shikai Zhang, Doctor/Researcher

Institute of Industry and Design, Lishui University, China

References

1. Shikai Zhang, “UNB Modulation Salvages Spectrum,” Microwaves & RF.

2. S.K. Zhang, “Bandwidth Efficiency Analysis of UNB Modulation Schemes,” Proceedings of the 4th International Conference on Wireless Communications, Networking, and Mobile Computing 2008 (Wicom 2008), October 12-17, 2008, Dalian, China.

3. H.R.Walker, “Making the Most of Ultranarrowband Modulation,” Microwaves & RF

4. H.R. Walker, “Sidebands Are Not Necessary,” Microwaves & RF.

5. H.R. Walker, Ultra Narrow Band Modulation Textbook, 2013.

6. Shikai Zhang, “Study on the General Design Scheme of UNB Modulation Formats,” Vol.70, No. 4, Wireless Personal Communications, Vol. 70, No. 4, 2013, pp. 1771-1791 (DOI 10.1007/211277-012-0780-6).

7. Shikai Zhang, “Assessing Different Ultranarrowband Formats,” Microwaves & RF.

8. Shikai Zhang, “High Efficiency Variable Phase PPK Modulation Scheme,” PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), R. 88 NR 7b/2012.

9. Steven Charles Hemple, “Analysis and Simulation of Wireless OFDM Communications,” Ph. D. thesis, San Diego State University, San Diego, CA, April 3, 2012.