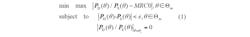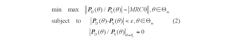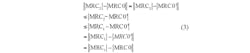Method Eases Monopulse System Jamming
Mainlobe jamming can pose problems for radar systems employing conventional adaptive monopulse techniques. Fortunately, relief is available through an approach that combines adaptive principles and convex programming. The technique can minimize the effects of composite mainlobe and/or sidelobe jamming while preserving a monopulse radar system’s capabilities to accurately estimate target angle.
Conventional adaptive monopulse systems can overcome the effects of sidelobe jamming and achieve acceptable output signal to interference and noise ratio (SINR) performance, but mainlobe jamming can be troublesome. While mainlobe jamming exists, both target and jammer signals appear within the system’s mainlobe.
This file type includes high resolution graphics and schematics when applicable.
In a conventional adaptive monopulse radar system, sum and difference beams must be adapted to reject the effects of a jammer. Such adapted sum and difference beams can distort and invalidate the monopulse response curve (MRC). An important part of adaptive monopulse radar design is suppression of mainlobe jamming while preserving undistorted MRC performance.
To suppress mainlobe jamming, a method based on a block matrix and beamforming algorithm has been used1,2 that requires large matrix eigenvalue decomposition, inverse matrix operations, and various other complex operations. Other researchers3-5 have suggested that reconfiguring the original array into subarrays can improve performance, although such a practice can lead to increased computational requirements. Techniques developed for use with linear arrays have assumed unrealistic uncorrelated azimuth and elevation estimates when applied to planar arrays.
A class of adaptive monopulse algorithms based on constraint methods has been proposed previously,6-8 capable of minimizing the effects of sidelobe jammers on monopulse systems while preserving MRC performance. However, these studies have shown poor angle estimation accuracy in the region near the mainlobe jammer angle. In earlier studies,9-11 convex programming was employed in monopulse systems for optimal beam pattern synthesis. Although the approaches obtained acceptable sum and difference beams, they did not address the problems of mainlobe jamming.
Considering that monopulse radar systems must overcome signals from mainlobe and sidelobe jammers, an approach of interest for adaptive monopulse systems can help improve performance by using a desired MRC response in the mainlobe region with anti-jamming characteristics in the sidelobe region. The new algorithm utilizes both the adaptive beamforming principle and convex programming for canceling the mainlobe jamming and sidelobe jamming while maintaining high monopulse angle estimation precision.
The Technique at Work
The performance of a monopulse radar system degrades severely in the presence of sidelobe jamming and/or mainlobe jamming. If not effectively suppressed, interference from these jammers can block target detection and tracking functions. As a solution, adaptive processing represents a class of processors that typically requires solving for weight vectors optimal in the mean square output of the processor. According to the principle of a minimum power distortionless response (MPDR), the optimal weight vector is given by12:
W = [R–1ά(θs)]/ά(θs)HR–1ά(θs)
where:
R = the covariance matrix of the antenna receiving data
and:
ά(θs) = the steering vector of the target angle.
However, the MRC can be seriously distorted if using a conventional adaptive method to suppress mainlobe jamming. This problem is addressed here through the use of adaptive beamformng and convex programming for handling the effects of mainlobe and sidelobe jamming signals.
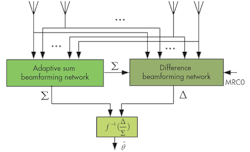
Figure 1 shows the basic idea of combining adaptive beamforming and convex programming for monopulse angle estimation. It is assumed that there is no jamming in the antenna receiving data. The desired monopulse response curve, MRC0, is obtained by the conventional method. An adaptive sub-beamforming network cancels interference from multiple sources within the sidelobes or mainlobes of the system’s antenna beam. Then the sum beam, Σ, and the desired response curve, MRC0, are transferred to a difference-beamforming network.
Convex programming is employed to construct a difference beam with the constraints that the difference-to-sum beam ratio must be close to MRC0 in the mainlobe region while the difference beam will approximate the sum beam in the sidelobe region. Finally, the resulting sum beam, Σ, and the difference beam, Δ, derived from the weight vectors, WS and WD, respectively, can be used to estimate the angle of the illuminated target.
In brief, this proposed monopulse radar system method employs convex programming to maintain desirable target response characteristics while minimizing the effects of jamming in the sidelobe and/or mainlobe regions. A key to achieving success with this approach is synthesis of the difference beam and how well it approximates a desired pattern. This can be measured in several ways, but least-squares analysis is used in this report.
To obtain an unbiased angle estimation for the target, the monopulse response curve should pass through the coordinate (θs, 0). So, additional constraint must be provided at the desired target direction. The difference pattern synthesis problem is stated in:
where:
Θm = the mainlobe region
Θs = the mainlobe region
and:
ε = a nonnegative real value.
In general, the ratio PD/PS is a complex value including both magnitude and phase responses. Once a target is not in the direction of monopulse radar beam illumination, an error voltage can be obtained from monopulse ratio analysis. That is, the error value depends on the magnitude of MRC, and it is unrelated to the phase of MRC.
When there is no phase requirement for the monopulse response within the mainlobe region, the problem of the difference pattern then can be stated by:
As a consequence, much better performance levels are expected when only magnitude is involved.10 It should be noted that Equation 1 can be rewritten as Equation 2.
The resulting optimization problem is nonconvex. Therefore, the difference pattern cannot be synthesized directly by classic convex optimization approaches. The optimality is guaranteed only to a locally optimal solution, while global optimality cannot be guaranteed.
In this section, an iterative algorithm is introduced to solve it by iteratively solving a convex optimization problem. At each iterative solution, the convex optimization problem can be formulated in the form of a second-order cone program (SOCP) for the solution.
A Four-Step Process
For the desired MRC response difference pattern synthesis problem, the specific phase of the desired MRC response is unknown. The phase of the MRC can be modified to create the desired MRC. The difference pattern synthesis problem described in Equation 2 can be solved by iteratively refining a suitable phase and then solving for Equation 1. This iterative algorithm can be described as a four-step process.
In the first step, an artificial “desired” phase (e.g., zero phase) is constructed for MRC0, since there is no phase requirement for the monopulse response within the mainlobe region. Find an initialization of optimal weight vector WD1 and the resulting monopulse ratio curve MRC1 = PD1/PS by solving Equation 1, where PD1 = WD1TV and PS is obtained by the adaptive sum beamforming network.
In the second step, the phase of MRC1 (such as ∠MRC1) is used to define a new desired MRC as:
MRC0′ = |MRC0|exp[j∠|MRC1|]
The new optimal weight vector WD2 can be found by solving Equation 1. The resulting difference beam and MRC are PD1 = WD2TV and MRC2 = PD2/PS, respectively.
In the third step, with the new desired monopulse ratio curve response, MRC0′, a new optimal weight vector, WD2, can be calculated according to Equation 1. The results can be obtained for the expressions:
PD2 = WD2TV
and:
MRC2 = PD2/PS.
Compared with MRC1, MRC2 is more approximate to the desired response MRC0′ due to the optimal solution.
The final step of the iterative algorithm involves returning to step 2 until the best attainable monopulse ratio curve response has been found.
The convergence of the iterations follows from the following sequence of inequalities shown in:
The first and the last equalities follow from the fact that MRC0 and MRC0′ have the same magnitude. The second inequality follows from the triangle inequality for complex numbers. The third inequality follows from the fact that WD2 is the global optimizer of Equation 1. The last equality follows from the fact that MRC1 and MRC0 have the same phase.
The Technique Demonstrated
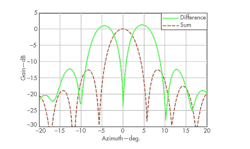
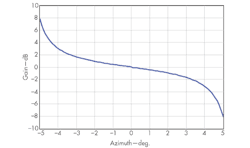
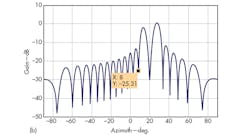
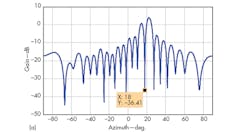
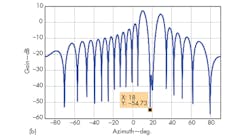
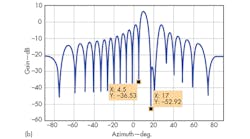
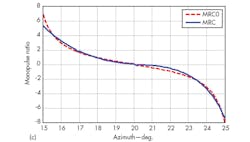
For demonstration purposes, assume that the incoming angle of a desired target is 20 deg. and the signal-to-noise ratio (SNR) is 0 dB. Also assume that mainlobe and sidelobe jammers with a 30-dB power difference are located at 4.5 and 17.0 deg., respectively. Via the adaptive monopulse technique proposed, the sum and difference patterns form nulls strips along the directions of jammers (Fig. 2), and a monopulse response curve leading to minimal distortion (Fig. 3) can be predicted.
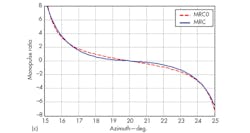
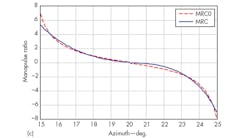
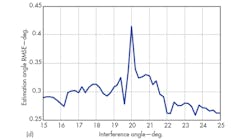
The angle estimation performance of this proposed approach can be evaluated by means of root mean square error (RMSE) analysis. Performing 300 Monte Carlo experiments with the statistical average of the desired target fixed at 20 deg., the jamming angle is scanned from 15 to 25 deg. in 0.1-deg. steps within the mainlobe region. Figure 4 provides the target angle estimation RMSE.
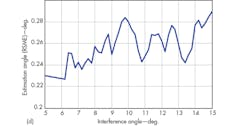
Figure 5 shows the target angle estimation RMSE when varying the interference angle from 5 to 15 deg. within the sidelobe region.
The RMSE for angle estimation will be somewhat larger than that for sidelobe jamming, especially when the jamming signal angle is approximately the same as the target angle. But as a whole, this monopulse anti-jamming approach provides acceptable RMSE for angle estimation while still suppressing mainlobe jamming (Fig. 6).
By applying a desired MRC response, this new approach can enhance the performance of monopulse radar systems, minimizing the effects of mainlobe jamming while maintaining high target detection accuracy. It does so by synthesizing the difference beam pattern with the constraint of matching the desired MRC.
This array pattern synthesis represents a nonconvex problem that is implemented via an iterative processes for convex optimization. At each iterative calculation, the convex optimization problem is formulated in the form of a SOCP. As simulation results show, the proposed technique effectively cancels the effects of mainlobe jammers on monopulse systems while delivering excellent target angle estimation accuracy.
References
1. B.W. Su, B.L. Wang, R.F. Li, and L.Z. Zhou, “Mainlobe interference canceling method via block matrix,” System Engineering and Electronics, Vol. 27, No. 11, pp. 1830-1832, 2005.
2. R.F. Li, Y.L. Wang, and S.H. Wan, “Research of reshaping adapted pattern under mainlobe interference conditions,” Modern Radar, Vol. 24, No. 3, 2005, pp. 50-53.
3. H. Hang and Z. Hao, “An improved two-stage processing approach of adaptive monopulse at subarray level,” Acta Electronica Sinica, Vol. 37, No. 9, 2009, pp. 1996-2003.
4. U. Nickel, “Monopulse estimation with subarray-adaptive arrays and arbitrary sum and difference beams,” IEE Proceedings Radar, Sonar & Navigation, Vol. 143, No. 4, 1996, pp. 232-238.
5. K.B. Yu, “Adaptive digital beamforming for angle estimation in jamming,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 37, No. 2, 2001, pp. 508-522.
6. C. Rao, R.F. Li, and L.Y. Dai, “Monopulse estimation with multi-point constrained adaptation in mainlobe jamming,” 2011 IEEE CIE International Conference on Radar, Chengdu 2011.
7. C. Rao and R.F. Li, “Multipoint constraint adaptive monopulse estimation in the presence of mainlobe jamming,” Radar Science and Technology, Vol. 9, No. 3, 2011, pp. 232-236.
8. R.L. Fante, “Synthesis of adaptive monopulse patterns,” IEEE Transactions on Antennas and Propagation, Vol. 47, No. 5, 1999, pp. 773-774.
9. M. D’Urso, T. Isernia, and E.F. Meliado, “An effective hybrid approach for the optimal synthesis of monopulse antennas,” IEEE Transactions on Antennas and Propagation, Vol. 55, No. 4, 2007, pp. 1059-1066.
10. P.J. Kajenski, “Phase-only monopulse pattern notching via semidefinite programming,” Antennas and Propagation Society International Symposium (APSURSI), 2012 IEEE, Chiago, Ill., 2012.
11. L. Manica, P. Rocca, M. Benedetti, and A. Massa, “A Fast Graph-Searching Algorithm Enabling the Efficient Synthesis of Sub-Arrayed Planar Monopulse Antennas,” IEEE Transactions on Antennas and Propagation, Vol. 57, No. 3, 2009, pp. 652-663.
12. B. Cantrell, “Development of a digital array radar (DAR),” IEEE Aerospace and Electronic Systems Magazine, Vol. 17, No. 3, 2002, pp. 22-27.