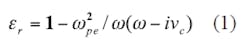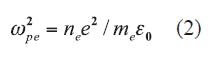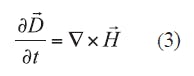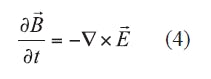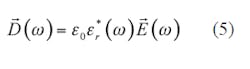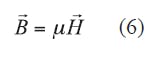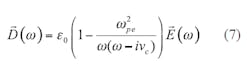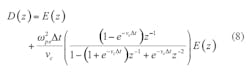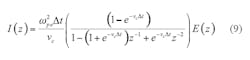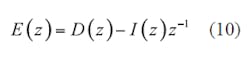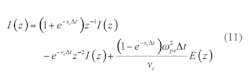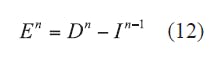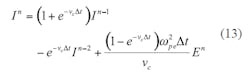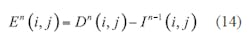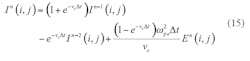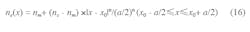Analyze The RCS Of A Plasma Antenna
This file type includes high resolution graphics and schematics.
Plasma antennas offer some special qualities that make them attractive for electronic-warfare (EW), radar, and other applications that may require stealth operation. The plasma in these antennas is essentially a blend of electrons, ions, and neutrons. When the density of the plasma is high enough, an electromagnetic (EM) wave will travel on its surface rather than deep into it. The plasma will exhibit the properties of a conductor, serving as an antenna for transmitting and receiving signals.
Consequently, a plasma column can be used as a radiative element in place of a metallic conductor. The plasma becomes conductive when energized by an RF source, and nonconductive once the source is removed. As a result, it can be made to have a radar cross section (RCS) that virtually disappears to an enemy radar once the RF source is removed.1 Another advantage of a plasma antenna compared with its metal counterpart is that it can be reconfigured; its radiation characteristics can be changed conveniently by electrical rather than mechanical control.2
Related Articles
• Modifications Improve Reflectarray Antennas
• MIMO/Diversity Antenna Serves Multiple Applications
• Helical Antenna Links GSM/UMTS
Much study has focused on plasma antennas—mainly to understand their radiation characteristics, including the input impedance, the radiation pattern, and the loss of the plasma column by means of analytical solutions or numerical simulations.3-5 Because a plasma antenna has little or no RCS when it is turned off, it has had great appeal for defense applications. But when it is on, whether transmitting or receiving, it does have an RCS and can be detected by an enemy radar. Understanding its RCS characteristics when it is powered on is important for applying these antennas to stealth applications.
Unfortunately, of the studies performed so far on plasma antennas, none has addressed the RCS characteristics of these antennas. As is known, plasma is a dispersive media for which the relative permittivity is dependent upon frequency. Various approaches can be used to simulate the interaction of EM waves with a plasma antenna. The two main methods based on finite-difference-time-domain (FDTD) analysis are the direct integration and the recursive convolution methods. Yoonjae Lee6 and Fan Luo7 studied the radiation characteristics of plasma antennas using the former method. Xue-Shi Li8 investigated the input impedance and radiation patterns of plasma antennas with nonuniform distribution of the plasma using the latter method. But neither addressed scattering fields from plasma antennas.
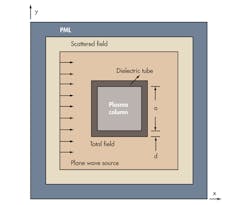
In the present study, FDTD analysis using the Z-transform will be applied for simulating the interaction of EM waves and an unmagnetized plasma antenna. Considering a plasma antenna as an infinite square column with a dielectric tube, it can be simulated by means of iterative formulas. The simulations can be applied to analyze the antenna’s RCS characteristics in terms of inhomogeneous plasma density, different EM incident frequencies, different plasma collision frequencies, and different relative dielectric constants for the tube containing the plasma.
Unmagnetized cold plasma is a dispersive material, with an effective relative dielectric constant, εr, given by Eqs. 1 and 29:
where:
vc = the electron-neutral collision frequency;
wpe = the plasma angle frequency;
w = the angle frequency of the incident EM wave;
ne = the plasma density;
e = the electron charge; and
me = the mass of the electron.
The complete set of Maxwell’s equations forunmagnetized cold plasma is given by Eqs. 3-6:
Note that Eq. 3 is written in the frequency domain and must be translated into the time domain for implementation into FDTD analysis. Substituting Eq. 1 into Eq. 5 yields Eq. 7:
By the convention theorem,10 the Z transform of Eq. 5 becomes Eq. 8:
Introducing an auxiliary term:
E(z) can be solved as shown in Eqs. 10 and 11:
As a result, the iterative formulas for FDTD are shown in Eqs. 12 and 13:
Equation 12 and 13 apply to one-dimensional space. They can be extended to two-dimensional use by means of Eqs. 14 and 15:
This file type includes high resolution graphics and schematics.
Achieving A Stealth State
This file type includes high resolution graphics and schematics.
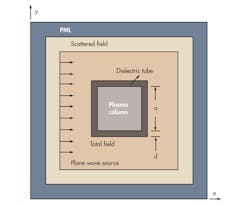
Achieving a stealth state is an important capability of a plasma antenna that sets it apart from traditional antennas. When the RF source is off, a plasma antenna will revert to a dielectric tube with a small RCS, and EM scattering from the tube can be neglected. But when the RF source is active, a plasma antenna is much like a metal antenna—transmitting and receiving signals—and it will have an RCS that is visible to detection. Figure 1 shows an infinite unmagnetized cold plasma column with a dielectric tube for a plane incident wave in the direction of the positive x axis.
1. A plasma antenna can be modeled by surrounding the plasma with a dielectric tube and using FDTD analysis.
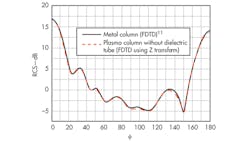
To demonstrate the use of the iterative formulas for FDTD based on the Z-transform, the RCS of a plasma column can be computed without the dielectric tube, when the frequency of the incident EM wave is much less than the operating frequency of the plasma. In such a case, the incident EM waves will interact with the plasma column, with the column behaving like a perfect conductor. Using a simplified two-dimensional (2D) model, the plasma column is simulated with an incident wave having a wavelength, λ, of 0.03 m, the side of the square column being equal to 2λ, the plasma density, ne, equal to 7.5 x 1018/m3 and the electron-neutral collision frequency, vc, equal to 5 x 109 Hz. Figure 2 shows that the RCS of a plasma column with high plasma density complies with the results for a perfecting conducting column.
2. These curves represent RCSs for a metal column and a plasma column without a dielectric tube.
Since plasma is a kind of ionized gas, a plasma antenna is typically molded with the help of a dielectric tube. Of course, the permittivity of a dielectric tube will have an impact and reduce the RCS of a plasma antenna. For a model of a plasma antenna with a dielectric tube, the key parameters are: the frequency of the incident wave, fin = 1 x 1010 Hz, the plasma density, ne = 1.3 x 1017/m3, the electron-neutral collision frequency, vc = 5 x 109 Hz, the side of the square plasma column, a =1.5 cm, and the thickness of the dielectric tube, d = 0.15 cm. Since the dielectric tube is part of the plasma antenna, impedance matching between the air and plasma is further deteriorated.
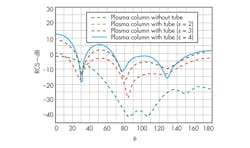
3. These curves show RCSs for a plasma column without surrounding dielectric and for plasma columns with a number of different relative dielectric constants.
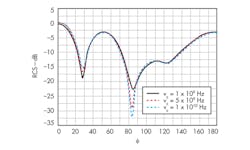
As Fig. 3 shows, when the dielectric tube is absent, the backscattering cross section of the plasma column decreases; the backscattering cross section for the plasma column with the dielectric tube present increases with decreasing permittivity. For a case where fin = 1 x 1010 Hz, ne = 1.3 x 1017/m3, a = 1.5 cm, d = 0.15 cm, and the relative dielectric constant of the dielectric tube is ε = 2.0, Fig. 4 shows that the collision frequency has only a minor impact on the backscattering cross section for a plasma column with dielectric tube.
4. The RCSs of a plasma column with a dielectric tube are shown for various plasma collision frequencies.
As Fig. 2 indicates, a plasma column acts as a perfect conductor if the frequency of an impacting EM wave (such as from an outside radar system) is much greater than the operating frequency of the plasma antenna, resulting in a large RCS from the antenna. If the plasma density is reduced by controlling the excitation source, the RCS of the plasma antenna will decrease significantly (as in Figs. 3 and 4). This is because the plasma antenna may be functional in a low-frequency range when the plasma density is smaller, and the plasma will act as a lossy medium, absorbing and scattering an EM wave from a radar transmitter, and the RCS of the plasma antenna will be reduced. Even with low density, a plasma antenna can normally transmit and receive signals. The characteristic plasma density is that required at a certain value to maintain a plasma column working as an antenna, To reduce the RCS, it is necessary to model the distribution function of the plasma density with reasonable accuracy. That density can be computed with the aid of Eq. 1612:
where:
ne = the electron density;
nr = 5 x 15 m-3 is the characteristic plasma density for the plasma antenna; and
nm = 1.3 x1018 m-3 to maximize the electron density of the plasma antenna.
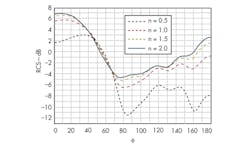
5. The RCSs of a plasma column with inhomogeneous plasma in a dielectric tube are shown for different electron densities.
Related Articles
• Modifications Improve Reflectarray Antennas
• MIMO/Diversity Antenna Serves Multiple Applications
• Helical Antenna Links GSM/UMTS
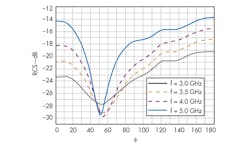
Assuming fin = 1 x 1010 Hz, vc = 5 x 109 Hz, ε = 2, a = 1.5 cm, and d = 0.15 cm, Fig. 5 shows the RCS of a plasma column with inhomogeneous plasma having different electron densities (n = 0.5, 1, 1.5, and 2). Fig. 5 indicates that as the value of n decreases, it has greater impact on reducing the antenna’s RCS. For a case where nc = 5 x 1015, nm = 1.12 x 1017 (a plasma frequency, fpe, of 3 GHz), vc = 5 x 109 Hz, ε = 2, a = 1.5 cm, and d = 0.15 cm. Figure 6 shows the RCS for a plasma column for different EM wave frequencies (fin = 3.0, 3.5, 4.0, and 5.0 GHz).
6. The RCSs of a plasma column with inhomogeneous plasma in a dielectric tube are shown for different incident EM frequencies.
As Fig. 6 shows, different EM wave frequencies have different capabilities of absorption for a distribution of inhomogeneous plasma density. When the frequency of the incident EM waves approaches the upper limit of the plasma frequency, attenuation of the incident EM waves increases due to the absorption of EM waves by the plasma resonance.
Acknowledgments
This work was supported by the Natural Science Foundation Project of Chongqing (CSTC 2010BB2202 and cstcjjA40013) and the Foundation of Chongqing Educational Committee (KJ120532), People’s Republic of China.
References
1. G.G. Borg, J.H. Harris,and N.M. Martin, “Plasmas as antennas: Theory, experiment, and applications,” Physics of Plasmas, Vol. 7, No. 7, 2000, pp. 2198-2202.
2. Kumar, Rajneesh Bora,and Dhiraj, “A reconfigurable plasma antenna,” Journal of Applied Physics, Vol. 107, No. 5, 2010, pp. 053303.
3. Ding Qian, et al., “On Characteristics of a Plasma Column Antenna,” ICMMT 2008, 2008, pp. 413-415.
4. Guo-Sheng Liu, Yang Shi-Ming, and Li Wei-Ming, “A mathematical modeling and analysis of plasma antenna,” The 4th Asia-Pacific Conference on Environmental Electromagnetics, 2006, pp. 706-709.
5. Xue-Shi Li and Bin-Jie Hu, “FDTD Analysis of a Magneto-Plasma Antenna with Uniform or Nonuniform Distribution,” IEEE Antennas and Wireless Propagation Letters, Vol. 9, 2010, pp.175-178.
6. Y. Lee and S. Ganguly, “Analysis of a PlasmaColumn Antenna UsingFDTD Method,” Microwave and Optical Technology Letters, Vol. 46, No. 3,2005, pp. 252-259.
7. Fan Luoand Bin-Jie Hu, “FDTD Analysis for Radiated Performance of a Cylinder Plasma Antenna,” The 8th International Symposium on Antennas, Propagation, and EM Theory,2008, pp. 803-806.
8. Xue-Shi Li, Fan Luo, and Bin-Jie Hu, “FDTD Analysis of Radiation Performance of a Cylinder Plasma Antenna,” IEEE Antennas and Wireless Propagation Letters, Vol. 8, 2009, pp.756-758.
9. M.A. Lieberman and A.J. Lichtenberg, Principles of Plasma Discharges and Materials Processing, Wiley, New York, 2005.
10. D.M. Sullivan, “Z transform theory and the FDTD method,” IEEE Transactions on Transactions on Antennas and Propagation, Vol. AP-44, 1996, pp. 28-34.
11. D.B. Guo and Y.B. Yan, Finite-Different Time-Domain Method for Electromagnetic Waves, 2nd ed., Publishing House of Xidian University, Xi’an, People’s Republic of China, 2005.
12. J.P. Rayner and A.P.Whichello, “Physical characteristics of Plasma antennas,” IEEE Transactions on Plasma Science,Vol. 32, No. 1, 2004, pp. 269-281.
This file type includes high resolution graphics and schematics.