Orthogonal frequency division multiplexing (OFDM) is a favored transmission scheme for many RF/microwave communications systems. It is both efficient and robust, even within a signal environment laden with interference and multipath signals, and is readily scalable in terms of number of users and bandwidth. Given the capabilities of modern application-specific integrated circuits (ASICs) and field-programmable gate arrays (FPGAs), the digital signal processing (DSP) needed to make OFDM work is not a barrier.
However, the analog technologies required for OFDM radios can still pose serious design challenges, especially when application requirements call for large numbers of OFDM radios within small enclosures at low cost and power consumption. Analog approaches cannot be upgraded as readily or quickly as digital technologies and, as a result, many basic performance parameters still present complex engineering tradeoffs. One of the more critical analog performance parameters, for example, is phase noise. It is especially relevant in OFDM radios due to the large number of closely spaced subcarriers. These subcarriers overlap in the frequency domain, with spectral peaks and nulls arranged to maintain orthogonality. Phase noise spreads the subcarrier energy—reducing orthogonality—and the resulting intercarrier interference impairs multiplexing and demodulation.
Signal generators perform multiple roles in OFDM system design, and optimizing their use speeds the design process. Modern signal generators can produce modulated and fully coded signals to test receivers, as well as continuous-wave (CW) signals to substitute for frequency references and synthesizers. In both cases, they provide the biggest benefit when they can generate both ideal signals and those which have specific imperfections. Ideal signals provide a reference to isolate and quantify the performance of other elements in the system, while deliberately imperfect signals allow the engineer to evaluate system performance in a “just good enough” scenario or a situation with known operating margins in terms of performance. Quickly and reliably arriving at performance that is “just good enough” is the designer’s goal, meeting system specifications while minimizing multiple cost factors.
System architects are aware of the phase-noise challenges of OFDM and, accordingly, structure signals to minimize the problem. The primary mechanism is known as pilot tracking, where selected subcarriers at some (but not necessarily all) symbol times transmit reference signals instead of payload data. The transmitted values of the pilot signals, such as their amplitude/phase or in-phase/quadrature (I/Q) values, are known at the system receiver. In calculating received values, the receiver will derive the corrections necessary to apply to the data subcarrier signals. The pilot signals are analogous to a training sequence for an equalizer, where some payload capacity is sacrificed to the transmission of a known signal, and the parameters derived by the receiver to correct the known portion of the signal are applied to the entire signal.
Figure 1 shows an example where the phase noise in the transmitted signal (including the pilot signals) is “tracked out.” The received signal can be continuously corrected across the full channel bandwidth, since the pilots are spread across the subcarriers in frequency and the symbols in time, allowing corrections to be applied. For example, a vector signal analyzer (VSA) can show the signal phase portion of “common pilot error,” making it possible to isolate and remove a great deal of the phase-noise error power.
1. These displays show the impact of I/Q correction on an OFDM constellation, before (left) and after (right) being applied to correct pilot and payload symbols. Both plots are shown with 312.5-kHz resolution bandwidth.
Of course, an engineer hoping to improve OFDM communications system performance needs to know which portion of the phase-noise power can and should be removed. A basic rule of thumb is that pilot tracking is effective for frequency offsets from 0% to about 10% of the subcarrier spacing. Assuming that the phase noise at frequency offsets wider than the channel will also be filtered out, the contribution of phase noise power to signal error can be given as:
EVM (dB) = [integrated SSB phase noise (0 to 100% of subcarrier spacing)] + [3 dB]
where the integrated phase noise is in dBc/Hz relative to the carrier power, and 3 dB is added to convert the phase noise from single-sideband (SSB) phase-noise power to double-sideband (DSB) phase-noise power.
Signal analyzers with integrated phase-noise applications can readily make SSB measurements and integrate the detected power from those measurements over a desired bandwidth. For this calculation, the modulation error or error vector magnitude (EVM) is determined solely from the phase noise; the calculation is performed with the assumption that linear errors are removed by equalization, and that in this instance, nonlinear errors other than phase noise are not significant.
Real-world signals in an OFDM radio (especially those from low-cost, low-power circuits) can suffer significant levels of phase noise. To help designers make reasonable tradeoffs, it is helpful to generate both CW and modulated signals with known amounts of phase noise, and to use these signals to evaluate their impact on other circuits in the radio. The simplest approach to create signals with known amounts of phase noise is to use random noise to phase-modulate a signal generator. For the CW case, this approach produces a SSB phase-noise curve (Lf) with constant -20 dB/decade slope, as shown in Fig. 2. Any adjustments to frequency-modulation (FM) deviations will change the overall phase-noise level, but not the phase-noise slope. Where needed, this phase modulation can be added to digital modulation instead of CW signals, though the result will not be as readily verifiable as for the CW case shown above.
2. Using random (white) noise to phase-modulate an RF signal generator produces phase-noise sidebands with a constant slope of -20 dB/decade, although such a constant slope is not representative of real-world signal sources.
The uniform -20 dB/decade slope of the aforementioned example is not typical of phase-noise sidebands exhibited by high-frequency oscillators and frequency synthesizers typically found in OFDM systems. Because the frequency sensitivity of OFDM systems is not uniform as described above, a more realistic phase-noise generation technique is desirable for system design and verification.
Fortunately, the fast digital-signal-processing (DSP) capabilities provided by modern ASICs and FPGAs that make OFDM practical also make possible the generation of test signals with customized phase-noise performance. As an example, the N5182B MXG X-Series signal generator from Agilent Technologies employs real-time baseband signal generation which provides “phase-noise-injection” capability. The inherent phase noise of this signal generator is extremely low, providing plenty of margin for generating signals with customized phase noise curves—even when the curves represent oscillators or synthesizers with relatively low phase noise.
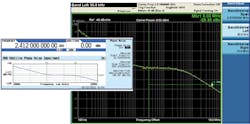
The phase-noise injection capability of the N5182B signal generator is designed to provide a variety of phase-noise curves while remaining simple to operate. Curves are configured as a close-in slope, a flat (with frequency) phase-noise pedestal, and resumption of a slope at wider offset frequencies descending to the signal generator’s broadband noise floor. Accordingly, only three parameters need to be set by the user: the end of the initial slope (f1), the beginning of the outer slope (f2), and the level of the pedestal. A constant slope of -20 dB/decade is assumed below f1 and above f2. Adjustment of the levels and inflection points allow the performance of different oscillators and synthesizers to be easily simulated.
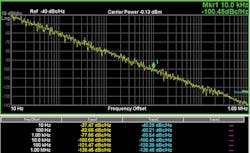
A basic IEEE 802.11g OFDM signal provides a good example of the effects of pilot tracking and the validity of calculating expected EVM from a customized phase-noise curve. The subcarrier spacing is the standard 312.5 kHz, and the 10% rule of thumb would suggest that phase noise within about 30 kHz of the carrier would be tracked out through demodulation relative to the pilot signals. In this example, the signal generator is programmed for a pedestal of -88 dBc/Hz between the 10- and 500-kHz inflection points, with the carrier set to 0 dBm for convenient calculations. An integrated SSB phase noise measurement of this signal produces a relevant phase-noise power of -29.35 dBc.
Figure 3 shows the signal generator’s phase-noise configuration screen reflecting these three parameters and a corresponding phase noise measurement. In this measurement, the integration bandwidth extends to 10 MHz (the widest offset measured), but the integrated power is dominated by the phase noise at narrower offsets (generally below about 5 MHz). Since the phase-noise power declines with frequency at a rate of 20 dB/decade, it becomes insignificant well before offsets reach the receiver’s nominal channel bandwidth of 20 MHz, or even the 10-MHz phase-noise measurement bandwidth.
3. Setting signal generator phase noise to a pedestal of -88 dBc/Hz between 10 and 500 kHz (left) produces integrated SSB phase noise (right) of -29.35 dBc over the relevant bandwidth of 30 kHz to 10 MHz. Integrating at offsets greater than 10 MHz would not result in appreciable additional power.
The final step in calculating expected EVM due to phase noise is to double the SSB power, thus arriving at the total phase-noise power in the receiver’s vulnerable bandwidth. Adding 3 dB to the measured -29.35-dBc phase-noise power suggests an EVM of -26.35 dBc, the result of the phase-noise contribution from the signal generator’s phase-noise injection.
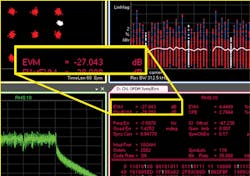
To measure the actual EVM, a signal analyzer with Agilent 89600 vector signal analyzer (VSA) software from Agilent Technologies is configured for normal IEEE 802.11g demodulation. The default setup enables phase tracking essential to remove phase noise. In addition, the demodulator should be configured for equalizer training that includes both the preamble and data, both to optimize equalizer effectiveness and provide the most accurate modulation quality results. Figure 4 shows the results.
4. The measured EVM of the signal impaired by phase noise correlates well with the estimate of -26.35 dB (-29.35 dB + 3 dB). The “10% of subcarrier spacing” guideline is thought to be slightly conservative, as shown in this example.
The measured results closely match the calculated estimate, especially since the 10% rule of thumb is generally regarded as slightly conservative. Since the bandwidth of the demodulator pilot tracking has a finite rolloff and the signal generator phase noise curve transitions gradually between slopes and the pedestal, the precision of the estimate is limited. Nonetheless, for situations where phase noise is a significant concern, this approach to simulating and estimating EVM in OFDM systems holds up well.
In summary, signal substitution is a proven approach for understanding and optimizing performance in complex RF systems. The use of signal substitution can help to speed the design process, reduce risk, and avoid the costs of producing an under- or over-performing radio. The ability to produce phase noise at specific levels and frequency distributions is especially beneficial for OFDM applications where frequency offsets matter.
Whether substituting for CW sources in the signal conversion chain or fully modulated signals at IF or RF, signal generators are a more powerful tool when they can produce both ideal and nonideal signals in which the imperfections are known and precisely controlled. Even for systems with complex tracking and correction capabilities, it’s possible to simulate typical impairments and accurately estimate their consequences by using signal generators with controlled phase noise.
Ben Zarlingo, Application Specialist
Agilent Technologies, Inc., Signal Analysis Operation, 1400 Fountaingrove Pkwy., Santa Rosa, CA 95403; (707) 528-2672, www.agilent.com
For additional reading
Bob Cutler, “Effects of Physical Layer Impairments on OFDM Systems,” RF Design, May 2002, p. 36.