In our blog on radar target modeling, we reviewed techniques for radar cross section (RCS) of simple point targets and extended targets with multiple scattering centers. We also noted we would review computational electromagnetic (EM) approaches that can be used for more accurate RCS predictions. That brings us to our next topic: benchmarking radar cross sections.
We start with an example that benchmarks the RCS computation on three popular structures: a square plate, a circular plate, and the NASA almond. For the square and circular plates, we compare the result with an analytical physical optics-based solution. For the NASA almond, a comparison is made with the Method of Moments (MoM) solution.
Square Plate RCS
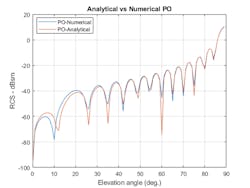
You can start with the physical dimensions for the square plate in addition to the wavelength and frequency for the analysis. The plate is defined using an STL file and is read into MATLAB using Antenna Toolbox. All dimensions are in meters.
L = 10.16e-2;
W = 10.16e-2;
p = platform;p.FileName = 'square_plate.stl';
p.Units = 'm';
The RCS computation is done in the elevation plane, in which the azimuth cut is 0 degrees. The electric-field polarization vector is set to a horizontal component on transmit and horizontal component on receive (referred to as HH polarization) for the RCS calculation. The results for the RCS computation using Antenna Toolbox are compared with the analytical results provided in the reference textbook, Radar System Analysis and Design Using MATLAB, by Bassem R. Mahafza.
The code to generate the data for the comparison is shown below. Note the rcs function used to calculate the numerical data. The platform in this example is the square plate defined by the variable p.
az = 0;
el = 0.05:1:90;sigma = rcs(p,f1,az,el,'Polarization','HH');
asigma1 = rectPlateRCS(L,W,f1,az,90-el);Figure 1 shows that the results compare closely, which is expected given the simple nature of the structure.
1. RCS for a square plate is depicted, revealing analytical results versus the numerical calculation method.
Circular Plate RCS
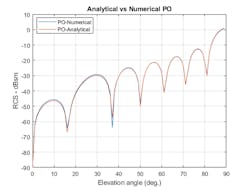
Let’s take a look at the same plot for a circular plate. Again, you can set the physical dimensions of the circular plate. It’s described using an STL file as follows:
R = 10.16e-2;
pc = platform;pc.FileName = 'circular_plate.stl';
pc.Units = 'm';
Again, the results from the RCS function in Antenna Toolbox are compared with results obtained from the analytical expression. The RCS calculation is done in the elevation plane between 0 and 90 degrees.
az = 0;
el = 0.05:1:90;sigmaV = rcs(pc,f1,az,el,'Polarization','HH');
asigma1 = circPlateRCS(R,f1,90-el);Figure 2 shows that the results again compare closely.
2. Here, RCS for a circular plate is reveals the analytical result versus the numerical calculation method.
NASA Almond
The third structure we look at is the NASA almond shape, which is also an important shape for benchmarking the performance of high-frequency EM solvers. The shape produces a large dynamic scattered field over large angular regions. The mathematical expressions in IEEE’s EM programmer’s notebook—benchmark radar targets for the validation of computational electromagnetics programs referencehave been used to create the STL file that describes the almond shape. Again, this structure can be brought into MATLAB as follows:
p = platform;p.FileName = 'NASA-Almond.stl';
p.Units = 'm';
Figure 3 shows the visualization of the NASA almond. Since the physical optics solver is only applicable at large ka values, we compare the results produced by Antenna Toolbox with those published in the previous reference.
3. Shown is the platform visualization of the NASA almond.
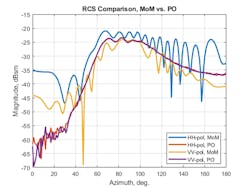
The results are produced by two solvers: the physical optics (PO) and the MoM. For this example, the wavelength for 7 GHz is approximately 4.3 cm. We refine the mesh used by the solver to be slightly finer than this using the λ/10. The mesh is defined in MATLAB as follows:
f2 = 7e9;m = mesh(p,'MaxEdgeLength',.0035)
az = 0:1:180;
el =0;
m =
struct with fields:
NumTriangles: 7878
NumTetrahedra: 0
NumBasis: []
MaxEdgeLength: 0.0035
MeshMode: 'manual'With this defined, we can calculate the RCS for the HH-polarization case, where both the transmitted and received fields are horizontally polarized.
sigmahh_po = rcs(p,f2,az,el,'Solver','PO',...
'EnableGPU', false,...
'Polarization','HH');
sigmahh_mom = rcs(p,f2,az,el,'Solver','MoM',...
'Polarization','HH');
Similarly, we calculate the RCS for the VV-polarization condition, where the transmitted and received fields are both vertically polarized.
sigmavv_po = rcs(p,f2,az,el,'Solver','PO',...
'EnableGPU', false,...
'Polarization','VV');
sigmavv_mom = rcs(p,f2,az,el,'Solver','MoM',...
'Polarization','VV');
Figure 4 shows the results from the two solvers for both polarization cases (HH and VV). Notice that the full-wave MoM solver extracts all of the phenomena that contribute to the scattered field. In contrast, the PO solver provides a first-order approximation and therefore is only able to predict the level of RCS. All variations at the different angles are averaged out. This is expected since the PO solver assumes that the surface current density outside the illuminated region does not contribute to the scattered field.
4. This RCS comparison of the NASA almond shows MoM and PO methods.
You have multiple techniques to model RCS in MATLAB. You can trade off the levels of fidelity of your model to match the requirements of your program.
To learn more about the topics covered in this blog, see the links below or email me at: [email protected].
- Modeling Target Radar Cross Section (example): Learn how to model radar targets with increasing levels of fidelity.
- Radar Cross Section Benchmarking (example): Learn about RCS benchmarking.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.