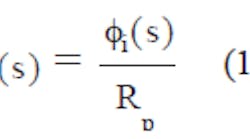Phase locked loops (PLLs) have been used for years to stabilize signal sources such as oscillators. In the past, loop bandwidths tended to be small compared to the sampling frequency, but with modern communications systems, requirements for faster switching times mean that this is no longer the case. Narrow-bandwidth PLLs can be effectively modeled and simulated by means of linear analysis, but these same approaches fall short for wide-bandwidth-sampled PLLs. In a sampled PLL, when the sampling frequency is large compared to the loop bandwidth, a linear simulation provides a fairly close approximation of the PLL's behavior. But when the loop bandwidth is a considerable percentage of the sampling frequency, as in fast-switching frequency synthesizers, linear analysis may not provide accurate predictions. This opening installment of a three-part article will explore a nonlinear approach to the analysis of the effects of sampling on PLL performance.
Figure 1 shows the essential components of a typical PLL in block-diagram form, with the reference phase, fr(s), given by Eq. 1:
There is an argument that the output phase, f?(s)/? and reference phase, fr(s), should already be sampled by the action of the PLL's dividers, However, this makes little difference since both sources of phase noise are synchronously resampled by the sampler that leaves the result unchanged, as shown by the equality in Eq. 2:
The sampled version of fe is described by Eqs. 3-5,
with the additional descriptions given in Eqs. 6, 7, and 8:
With a little rearrangement, it is possible to solve for the output phase as a function of the input noise
(see equation 9)
(see equation 10)
(see equation 11)
(see equation 12)
(see equation 13)
Putting f'o(s) into the expression for fo(s) results in Eq. 14. Note that throughout this article series, the "prime" symbol, such as in f'o(s), is used to denote a sampled signal.
At this point, this analysis will proceed to separate out the noise at the output due to reference noise and VCO noise. The first step is to find the noise due to the reference by means of Eq. 15:
where
for(s) = the output phase due to the reference, and can be found by Eqs. 16 and 17.
This is effectively the sampled reference noise modified by the transfer response of the loop.
Now, consider the contribution to output phase noise, fo, due to VCO noise, No(s)
It is now necessary to develop the mathematical functions for performing the phase-noise analysis. Let the impulse sampled f(t), f (t) be defined as in Eqs. 20 and
where T = 1/Fs.
This may be represented by the Fourier series
where
Now, call F'(s) the Laplace transform of the sampled time function, f'(t), where
F'(s) = L(f'(t))
Then, apply this to the reference noise:
Continue to page 2
Page Title
Note the sampled function has been multiplied by a factor of T. This is because in a sampled PLL design, this is taken into account by the phase detector.
The noise due to the VCO can be found from
where
Now take out the n = 0 term and add this to the sum of the rest. For n = 0
Combining the two results in Eq. 31:
Armed with these mathematical tools, it is now possible to substitute some component values that correspond to those used in the test PLL and observe the results. For example, for ?, the angular frequency, is 105001000000(2 π). The loop filter values for a standard charge-pumptype phase detector are shown in Fig. 2 and are R1 = 10 x 103; C1 = 18 x 10-9; and C2 = 2.7 x 10-9. The phase detector gain for the charge pump using 4 mA, Kpd, is Kpd = 4 x 10-3/2π . The phase detector comparison frequency of 25 kHz (sampling frequency, fs) is given as fs = 25 x 103. The reference divider ratio, Rp, is 672, and the sampling frequency, ?s, in radians, is ?s = 2πfs. The VCO gain in radians/s/V (for a VCO with a tuning sensitivity of 20 MHz/V), K?VCO = (2π )20 x 106. The loop division ratio, N, is 35200. The gain parameter, G(s), which includes the phase detector gain and the loop filter response, becomes
which simplifies to
with K(s) given by:
The overall forward gain, GK(s), which is the combination of oscillator gain and frequency response, and phase detector gain and loop filter frequency response, is found by Eq. 35:
The gain and phase responses for an open-loop continous-time PLL system can be seen in Figs. 3 and 4. Figure 3 shows the magnitude reponse versus frequency, while Fig. 4 shows a plot of open-loop phase versus frequency for a continuous-time PLL system.
Next month, this three-part series on the effects of sampling frequency on PLL performance will compare key characteristics of continuous-time PLL systems with sampled (discretetime) PLLs. To begin, the open-loop curves of Figs. 3 and 4 will be compared to closed-loop responses, and the analysis will delve deeper into the effects of sampling on PLL phase noise by examining PLL noise sources.