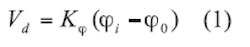Assemble A Ku-Band Frequency Synthesizer
Frequency synthesizers are an essential part of modern digital-microwave-radio (DMR) communications systems. With new ITU-R recommendations for DMR communications bands at 15, 18, 23, 38, and 55 GHz, frequency synthesizers are needed for use as local oscillators (LOs) for the frequency upconversion chores in transmitters and the frequency downconversion in receivers for a variety of different frequency architectures. The design of a Ku-band (14.4 to 15.5 GHz) frequency synthesizer offers practical benefits for several of these bands, since with multiplication by four it can be made to provide frequency coverage as high as 60 GHz. The programmable frequency synthesizer, which switches in 625-kHz steps and can be used with quadrature phase-shift-keying (QPSK) and quadrature-amplitudemodulation (QAM) transmission schemes, is a straightforward design that features low phase noise and reliable operation using commercially available oscillator and phase-lockloop (PLL) integrated circuits (ICs).
The PLL concept was developed in the 1920s.1 The technology has been widely used in a variety of communications systems but until recently, has been too costly and complicated for use in many consumer and industrial applications. But with the growing availability of PLL ICs, the technology is economical enough for most systems. One main area of interest for applying PLLs is in oscillators, to stabilize output frequencies and lower noise levels.2-4 In addition, DMRs represent a growing market for PLLs.
DMRs and other high-capacity digital communications systems require low-cost but high-quality frequency sources. Frequency synthesizers provide stable local oscillator (LO) signals for microwave transceivers, supporting frequency upconversion for transmit operation and frequency downconversion for receive operation. Synthesizer noise is particularly critical in such applications since a digital radio link is sensitive to phase noise.5-7 The phase noise is detected in such a system along with desired modulated signals. Excessive phase noise degrades the DMR system's biterror- rate (BER) performance.
A DMR system features at least two radios. Two channels of the licensed microwave band are used by each full-duplex system. One of the radio pair transmits on one channel and receives on the other, while the converse is true for the other radio (Fig. 1).
Availability of compact, low-cost PLL ICs has helped to reduce the cost and complexity in designing a frequency synthesizer.8-10 In a frequency synthesizer, the PLL is used to generate an output frequency that is some integer multiple of the input frequency. The PLL is in fact a nonlinear system, but can be modeled as a linear system across some of its operating regions. A basic PLL consists of a phase detector (PD), a low-pass filter (LPF), and a voltage-controlled oscillator (VCO) in its simplest form (Fig. 2). The nonlinearity of the PD makes the PLL a nonlinear device, although it can be modeled as a linear system with the loop locked. The PD's output voltage can be assumed to be proportional to the difference between the phases of the input signals, as represented in Eq. 1.11-15
where
Kφ = the gain coefficient of the PD in v/rad.
The VCO can also be modeled as a linear component; its output frequency deviates from the free resonance frequency by the Δω = K o V e value, where Ve is the output voltage of the LPF and KO is the gain coefficient of the VCO. Since frequency is a derivative of phase, the VCO's operation can be explained by Eq. 2.
Given these assumptions, the PLL can be linearly modeled as indicated in Fig. 3, where F(s) represents the transform function of the LPF. In Fig. 3, the output and reference frequencies are equal since there is no frequency divider in the loop.
By using a frequency divider in the feedback loop, it is possible to achieve the desired high-frequency output signal by setting a sufficiently large value for the frequency divider. The divider will produce a broadband output with high stability and relatively large frequency switching steps. By adding the frequency divider block in the feedback path, the general block diagram of a linear PLL will be in the form of Fig. 4. The output frequency can be obtained by applying Eq. 3.
A block diagram of the Ku-band frequency synthesizer shows generic circuit elements (resistors and capacitors) along with the main building blocks, such as the PD, reference crystal, loop filter, and VCO (Fig. 5). A temperature-compensated crystal oscillator (TCXO) is used to generate a 10-MHz reference frequency. The selected TCXO device has good phase noise and frequency stability. The notations fr and fin are used for the reference frequency and the frequency sample of VCO output, respectively. The PD chip consists of a phase/frequency detector and internal M and R digital frequency dividers. The M and R values are determined externally by a programmable microcontroller. The data is serial and is applied to the phase detector via three pins.
The PD receives the reference and VCO signals from related pins. After dividing the reference frequency by R and the VCO frequency by M, the resulting signals are compared. If the ratio of fin/M is greater than the ratio of fr/R, then the PD_U function is activated. Otherwise, the PD_D function will be activated. These two signals are applied to the loop filter to create the tuning voltage for the VCO. The loop filer is an active LPF; the tuning voltage depends on the PD_D and PD_D values.
The VCO is a monolithic-microwave- integrated-circuit (MMIC) device that adjusts output frequency according to a 0-to-10-V tuning range. It requires DC bias voltage of +5 VDC and supply current of 290 mA. The phase noise for the TCXO is relatively low when measured close to the carrier, at -70 dBc/Hz offset 1 Hz from the carrier. The phase noise drops as expeced with distance from the carrier, at -100 dBc/Hz offset 10 Hz from the carrier, -130 dBc/Hz offset 100 Hz, -145 dBc/Hz offset 1 kHz, and -150 dBc/Hz offset 10 kHz from the carrier.
The signal frequency of pin number 11 in the MMIC is equal to fout/8, where fout is the output signal frequency of the VCO at pin number 1. The signal at pin number 11 is used as a frequency sample of the VCO output signal at pin number 1. Note that it is necessary to amplify the sample signal before applying to the phase detector input (Fig. 5). In the fabricated synthesizer, the values of R and M are equal to 16 and 29009, respectively. The output frequency in the locked state can be found by applying Eq. 4
In a PLL, adding one unit to the value of M results in an increment in the output frequency. This increment is referred to as a frequency step, with the size of the step measured in frequency. For the Ku-band frequency synthesizer, the step size is equal to 625 kHz. In other words, the frequency synthesizer is tuned up and down in frequency in 625-kHz steps. The schematic diagram for the Ku-band PLL frequency synthesizer (Fig. 6) shows the main building blocks as well as the various circuit elements (resistors and capacitors) needed for fabrication. In the fabricated Ku-band frequency synthesizer, the VCO phase noise is equal to -80 dBc/Hz offset 10 kHz from the carrier. The phase noise of the TCXO is around -150 dBc/Hz, thus its effect on output signal will be equal to:
(PNout)ref = PNref + 10logM = 150
+10log(8 x 29009) = 96.34 dBc/Hz
As this shows, the noise of the VCO dominates the noise at the output of the frequency synthesizer. The output phase noise of the frequency synthesizer is a bit degraded relative to that of the VCO since the noise level from the oscillator is increased by passing through other parts of the PLL circuitry.
Continue to page 2
Page Title
In order to determine the singlesideband (SSB) phase noise of the Ku-band frequency synthesizer, measurements were performed with an HP8563A spectrum analyzer from Agilent Technologies. The frequency span was set to 50 kHz, with the resolution-bandwidth and video-bandwidth filters set to 1 kHz and 30 Hz, respectively (for more on the operation of a spectrum analyzer, refer to this month's inaugural RF Primer section on p. 38). The 43.33-dB power difference between the carrier signal and the 10 kHz offset leads to phase noise of 43.33 10log(resolution bandwidth) = 73.33 dBc/Hz.16-18
These measured results show the performance of the Ku-band synthesizer to be acceptable compared to performance levels available from commercially available synthesizer products designed for relatively narrowband applications. The measured results also agree closely with earlier predictions for the frequency synthesizer's phase-noise performance.
In short, the construction details presented for the Ku-band frequency synthesizer can be applied to produce a low-noise signal source that provides performance levels adequate to the needs of modern DMR-based communications systems. The performance of the synthesizer, as validated by spectrum-analyzer measurements, is what is expected based on model predictions. It is suitable for use in systems employing complex modulation formats typical of DMR-based systems, such as QPSK and QAM, with reliable operation and low phase noise. The performance levels allow frequency multiplication for use in higher-frequency systems. In addition, the design and construction details presented here, while having been used for fabricating an example Kuband frequency synthesizer, can also be applied to the design and construction of other frequency bands.
REFERENCES
1. E. V. Appleton, "Automatic Synchronization of Triode Oscillators," Proceedings of the Cambridge Philosophical Society, Vol. 21, Part 3 (1922-1923), p. 231.
2. Steve Maas, "Amplifiers and Oscilltors: The Landscape in 2007," Microwave Journal, April, 2007, pp. 24-44.
3. A. Chenakin, "Frequency Synthesis: Current Solutions and New Trends," Microwave Journal, May, 2007, pp. 256-266.
4. U. L. Rohde and A. K. Poddar, "Minimization of Phase Noise in Scaled Device Coupled Mode RF Oscillators," Microwave Journal, June, 2007, pp. 50-68.
5. G. D. Vendelin, A. M. Pavio, and U. L. Rohde, Microwave Circuit Design Using Linear and Nonlinear Techniques, Wiley, New York, 2005.
6. U. L. Rohde, A. K. Poddar, and G. Bock, The Design of Modern Microwave Oscillators for Wireless Applications: Theory and Optimization, Wiley, New York, 2005.
7. Ulrich L. Rohde, Microwave and Wireless Synthesizers, Wiley, New York, 1997.
8. Roland E. Best, Phase-Locked Loops: Design, Simulation, and Applications, 6th ed., McGraw-Hill, New York, 2007, 6th ed. 2007
9. Behzad Razavi, RF Microelectronics, Prentice-Hall, Englewood Cliffs, NJ, 1998.
10. P. R. Gray, P. J. Hurt, S. H. Lewis, and R. G. Meyer, Analysis and Design of Analog Integrated Circuits, 4th ed., Chap. 10, Wiley, New York, 2001.
11. James A. Crawford, Advanced Phase-Lock Techniques, Artech House, Norwood, MA, 2008.
12. James A. Crawford, Frequency Synthesizer Handbook, Artech House, Boston, MA, 1994.
13. W. F. Egan, Phase-Lock Basics, 2nd ed., Wiley, New York, 2008.
14. V. Manassewitsch, Frequency Synthesizer Theory and Design, Wiley, New York, 2005.
15. D. Banerjee, "PLL Performance, Simulation, and Design," Technical Note, National Semiconductor, Santa Clara, CA, 2006.
16. J. Grebenkemper, "Local Oscillator Phase Noise and its Effect On Receiver's Performance," Technical Note, W-J Communications, San Jose, CA.
17. V. F. Kroupa, "Noise Properties of PLL Systems," IEEE Transactions on Communications, Vol. Com-30, October 1982, pp. 2242-2252.
18. B. Biglarbegian, F. Hodjat Kashani, and H. Ameri, "A Low Phase Noise 18-GHz Band Frequency Synthesizer With Low Frequency Step Size," Proceedings of the International Conference in Computer and Communication Engineering (ICCCE'06), May 9-11, 2006, Kuala Lumpur, Malaysia, pp. 857-860.