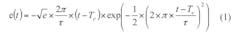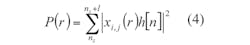UWB Imaging Aids Breast Cancer Detection
Ultrawideband (UWB) technology not only is useful for communications, it also provides the microwave imaging needed to detect small malignant tumors in the early stages of breast cancer. Details about tumors are found by comparing UWB signals propagating in a tumor-containing breast with UWB signals propagating in a tumor-free breast serving as the calibration device.
This current study explores a novel method of extracting the calibration waveform for breast cancer detection to remove any negative effects brought upon by the tumor-free model, especially for cases of actual clinical diagnosis when a tumor-free case cannot be obtained. The extracted calibration waveform will be used to provide correct tumor information in a reconstructed breast image.
This file type includes high resolution graphics and schematics when applicable.
Diagnostic Tools
Malignant breast cancer is a serious threat to women’s health, with early detection a powerful weapon in the fight against breast cancer. Magnetic resonance imaging (MRI) and x-ray mammography are among the most common breast screening tools. But limitations of various methods, such as safety issues associated with ionizing radiation and patient comfort, have led researchers to investigate other means of breast imaging.
Ultrawideband (UWB) microwave imaging may be the most promising new imaging approach since it is low in cost compared to MRI systems and noninvasive compared to x-ray analysis. UWB technology is typically applied to communicate information by means of short pulses.1 It supports high data rates across short distances with low power, primarily due to the wide bandwidths of its short pulses. UWB technology can be applied to cancer research on the basis of the contrast in electrical properties between malignant tumors and normal fatty breast tissues.2,3
A main challenge in detecting small malignant tumors using UWB microwave imaging is the strong backscatter from the breast skin, as well as other high-amplitude reflections from inside and outside the breast, which are orders of magnitude larger than the signals from the tumor. A new solution is proposed to solve this problem.
Signals received from a tumor-free model often are subtracted from those where a tumor exists.4-6 This approach can highlight reflections from objects of interest, but is not practical for clinical diagnosis since a tumor-free model may not always be available. One practical means of extracting calibration waveforms during detection uses a linear antenna array along different places on the surface of the breast. This approach eliminates the effects brought by the tumor-free model.
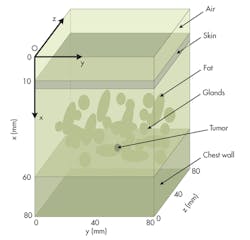
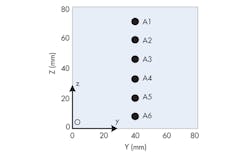
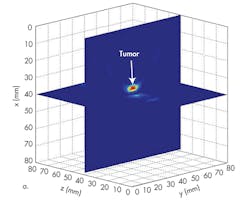
Three-dimensional (3D) configurations of a breast can be used for analysis by means of UWB microwave study (Fig. 1). This breast model is assumed to act like the real flattened breast of a supine patient involving the skin, fat, glandular tissue, chest wall, and tumor. A tumor of 5 mm diameter is assumed to be embedded in the breast. It is located at x = 40 mm, y = 40 mm, and z = 40 mm. The six-element antenna array is arranged to stay in a line on the surface of the breast configuration (Fig. 2).
During detection, a Gaussian monocycle pulse (GMP) is emitted from one emitter alternatively. The other five detectors collect the backscattered waveforms. The input GMP is defined by:7
where:
Tc = the time shift factor;
τ = 1/f0 = the impulse width; and
f0 = the center frequency.
A center frequency of 5 GHz is used in this study. Through repetition, signals are collected and used for image reconstruction. Backscattered signals are computed by using the finite-difference time-domain (FDTD) method. Both of the dispersive properties and the spatial heterogeneity of normal breast tissue are considered in the FDTD model.
The late time content of detected signals includes contributions from both the tumor and healthy breast tissue clutter signals, but also additional unwanted signals such as antenna coupling, reflections from the skin, or reflections from the array.8,9 Since these undesired signals have significant amplitude levels, they can hide the tumor response if a direct reconstruction is performed. During wave propagation, the signal amplitude is decreased largely due to the radical spreading of the impulse energy and the path loss in the breast tissue. To solve this problem, in a conventional study, the tumor response is extracted by subtracting calibration signals collected from a tumor-free case.10
However, a tumor-free reference is not always available, so an alternative approach has been developed to extract the tumor response from the noise signals. This way, those undesired effects can be eliminated by shifting the whole antenna array during detection. The tumor response can be obtained by subtracting the signals detected by the linear antenna array located at different places.
Analyzing The Results
The antenna array is located at y = 40 mm on the breast surface, at the center of the breast surface (Fig. 2, again). A Gaussian monocycle impulse is radiated from each antenna A1 to A6 separately and detected by the other five antennas simultaneously. Scattered signals from the breast tissue reflections, which also include the tumor response, then can be obtained. The whole antenna array is arranged to move in the y direction to y = 55 mm. Then, the detection procedure is repeated to obtain the other backscattered signals that also contain information about the tumor.
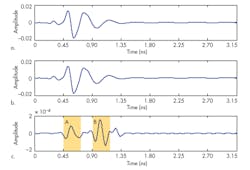
For example, Figure 3 shows detected signals in which antenna A1 emits the impulse while the antennas A3 detect the backscattered waves, with the antenna array at y = 40 mm and y = 55 mm. Figure 4 shows the detected signals in which antenna A1 emits the impulse and the antennas a6 detect the backscattered waves, with the antenna array at y = 40 mm and y = 55 mm. The two signal peaks in the shadowed portions A and B in Figure 3c are achieved by subtracting the signals detected by antenna A6 when the antenna array is located at y = 40 mm from signals detected when the antenna array is located at y = 55 mm.
The two signal peaks in the shadowed portions A and B of Figure 4c are obtained in the same way. Although the signals during the detecting propagation will include the clutters shown in the shadowed portion A, the signals shown in Figure 4c can be applied to reconstruct the tumor image using a signal-processing method that can strengthen the tumor response shown in the shadowed portion B and weaken the clutter noise in portion A.
na = the reference time to which every signal is aligned and is chosen to be the worst delay over all channels and physical locations.
In this way, the weighed signals xi,j(r) should be windowed with h[n] by Equation 3 to eliminate the effects of clutter. The window is chosen as:11,12
where:
l = the sample time in which the signals penetrate through the tumor.
The term xi,j is the amplitude value of the signal that has been delayed. The energy of the tumor point, r, can be determined by taking the sum of the square of the windowed signals:where:
P(r) = the energy vector of the tumor point, which can also be treated as pixels for image reconstruction.13
All subtracted signals that are achieved from the six antennas need these processes to enhance the scattered signals shown in the shadowed portion B. Meanwhile, the effects of the clutter signals of the tumor response in the shadowed portion A that exists in the useful signals can be decreased after these steps.
To maximize the tumor response and minimize the noise response, a double-constrained robust capon beamforming algorithm is applied in the image optimization stage to improve the clarity of the reconstructed image.14-16 These signals then can be used to form an image to know whether a tumor exists or not.
A breast image can be reconstructed based on the subtracted signals obtained by the six antennas, just like the signals shown in Figures 3c and 4c when the antenna array is located at y = 55 mm and y = 40 mm separately (Fig. 5). But applying signals detected by the antenna array at these two locations cannot provide full tumor information in the y direction (Fig. 5b). The antenna array must be moved along the y axis to improve resolution in the y direction. To do this, the tumor response was recorded with the antenna array at y = 40 mm, y = 45 mm, y = 50 mm, y = 55 mm, y = 60 mm, y = 65 mm, and y = 70 mm. With this many processing steps, high resolution can be achieved (Fig. 6).
Acknowledgments
The authors are grateful to the support of the National Natural Science Foundation of China (under Grant Number 61271323) and the open project from the State Key Laboratory of Millimeter Waves, China (under Grant Number K200913).
References
1. P.K. Saha, N. Sasaki, and Kikkawa Takamaro, “A Single-chip Gaussian Monocycle Pulse Transmitter using 0.18-µm CMOS Technology for Intra/Interchip UWB Communication,” 2006 Symposium on VLSI Circuits, Digest of Technical Papers, 2006, pp. 252-253.
2. X. Xiao and Kikkawa Takamaro, “Influence of the Organism Interface on the Breast Cancer Detection by UWB,” Applied Surface Science, Vol. 255, 2008, pp. 597-599.
3. Y. Zou and Z. Guo, “A Review of Electrical Impedance Techniques for Breast Cancer Detection,” Medical Engineering & Physics, Vol. 25, 2003, pp. 79-90.
4. X. Li and S.C. Hagness, “A Confocal Microwave Imaging Algorithm for Breast Cancer Detection,” IEEE Microwave And Wireless Components Letters, Vol. 11, 2001, p. 130.
5. Xia Xiao and Takamaro Kikkawa, “Extraction of Calibration Waveform for Confocal Microwave Imaging for Early Breast Cancer Detection,” IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies For Wireless Communications, 2007, pp. 1287-1290.
6. Y. Xie, B. Guo, L. Xu, J. Li, and P. Stoica, “Multistatic Adaptive Microwave Imaging for Early Breast Cancer Detection,” IEEE Transactions on Biomedical Engineering, Vol. 53, 2006, pp. 1647-1657.
7. Ahmed Maher, Abed Shaheen, and Kaydar M. Quboa, “Pole Splitting Algorithm for UWB Breast Cancer Imaging,” Proceedings of the 16th IEEE Mediterranean Electrotechnical Conference (MELECON), 2012, pp. 417-420.
8. Aslina Abu Bakar, Amin Abbosh, Philip Sharpe, M.E.Bialkowski, and Yifan Wang, “Heterogeneous Breast Phantom for Ultra Wideband Microwave Imaging,” Microwave and Optical Technology Letters, Vol. 53, No. 7, 2011, pp. 1595-1598.
9. Jean-Francois Deprez, Maciek Klemm, Penny Probert Smith, and Ian Craddock, “Twin Target Correction for Ultra-wideband Radar Imaging of Breast Tumors,” 2010 IEEE International Symposium on Biomedical Imaging, pp. 213-216.
10. T.F. Zanoon and M.Z. Abdullah, “Early stage breast cancer detection by means of time-domain ultra-wide-band sensing,” Measurement Science and Technology, Vol. 22, 2011, p. 13.
11. Martin O’Halloran, Edward Jones, and Martin Glavin, “Quasi-Multistatic MIST Beamforming for the Early Detection of Breast Cancer,” IEEE Transactions on Biomedical Engineering, Vol. 57, No. 4, 2010, pp. 830-839.
12. M. Guardiola, Francesco Colonna, Mariagrazia Graziano, Mario R. Casu, Xiaolu Guo, and Maurizio Zamboni, “Hardware Acceleration of Beamforming in a UWB Imaging Unit for Breast Cancer Detection,” VLSI Design, 2013, pp. 1-11.
13. Xiao Xia, Xu Li, and Li Qinwei, “A double constrained robust capon beamforming based imaging method for early breast cancer detection,” Chinese Physics B, Vol. 22, No. 9, 2013, pp. 1697-1704.
14. Liu Bingyu, Xiao Xia, and Liu Xu, “Ultra-wideband Microwave Image Reconstruction by Robust Capon Beamforming Algorithm for Early Breast Cancer Detection,” International Conference on Control, Automation and Systems Engineering, 2011, pp. 1-4, 1622-1625.
15. M. Guardiola, S. Capdevila, J. Romeu, and L. Jofre, “3D Microwave Magnitude Combined Tomography for Breast Cancer Detection Using Realistic Breast Models,” IEEE Antennas and Wireless Propagation Letters, 2012, p. 11.
16. Xu Li, Xiao Xia, and Kikkawa, “Ultra-wide-band microwave image reconstruction for early breast cancer detection by norm constrained capon beaming,” Mathematical and Computer Modeling, Vol. 58, 2013, pp. 403-408.