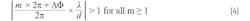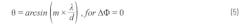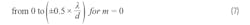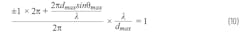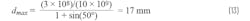Phased-Array Antenna Patterns (Part 4)—Grating Lobes
>> Microwaves & RF Resources
.. >> Library: Article Series
.. .. >> Topic: Phased-Array Antenna Design
.. ... .. >> Phased-Array Antenna Patterns
Download this article in PDF format.
In the first three parts of this series, we introduced the phased-array steering concept and looked at the influencers on array gain. In the next two parts, we’ll discuss grating lobes and beam squint. Grating lobes can be hard to visualize, so we’ll draw on their similarity with signal aliasing in digital converters, then use that to think of a grating lobe as a spatial alias.
In the upcoming Part 5, we’ll explore the issue of beam squint. Beam squint is an unfocusing of the antenna across frequency when we use phase shift, instead of a true time delay, to steer the beam. We’ll also discuss the tradeoff between these two steering methods and understand the impact of beam squint on typical systems.
An Introduction to Grating Lobes
So far, we have only examined the case in which the element spacing is d = λ/2. Figure 1 begins to illustrate why an element spacing of λ/2 is such a common metric in phased arrays. Two cases are shown. First, in blue, we show the same 30° plot from Part 3 of this article series. Next, the d/λ spacing is increased to 0.7 to show how the antenna pattern changes.
With this increase in spacing, note the reduction in the beamwidth, which is a positive result. The decreased spacing of nulls brings them closer together, which is also an acceptable result. But now there’s a second angle, in this case at –70°, where there’s full array gain. This is a most unfortunate result. This replica of antenna gain is defined as a grating lobe and can be considered spatial aliasing.
Analogy to Sampled Systems
An analogy useful in visualizing grating lobes is to think of aliasing in a sampled system. In an analog-to-digital converter (ADC), undersampling is often used when frequency-planning a receiver architecture. Undersampling involves purposefully reducing the sample rate (fS) such that the sampling process translates frequencies above fS/2 (the higher Nyquist zones) to appear as aliases in the first Nyquist zone. This causes those higher frequencies to appear as if they were at a lower frequency at the output of the ADC.
A similar analogy can be considered in phased arrays, where the elements spatially sample the wavefront. The Nyquist theorem can be extended to the spatial domain if we suggest that two samples—that is, elements—per wavelength are required to avoid aliasing. Therefore, if the element spacing is greater than λ/2, we can consider this spatial aliasing.
Calculating Where Grating Lobes Appear
But where will these spatial aliases (grating lobes) appear? Previously, we showed the phase shift applied to the elements across the array as a function of beam angle:
Inversely, we can compute the beam angle as a function of phase shift:
The arcsin function only produces real solutions for arguments between –1 and +1. Outside of these bounds, the solution isn’t real—the familiar “#NUM!” in spreadsheet software. Also note that the phase in Equation 2 is periodic and repeats every 2π. So, we could replace ∆Φ with (m × 2π + ∆Φ) in the beamsteering equation to yield Equation 3:
where m = 0, ±1, ±2, …
To avoid grating lobes, our goal is to obtain a single real solution. Mathematically, this is accomplished by keeping:
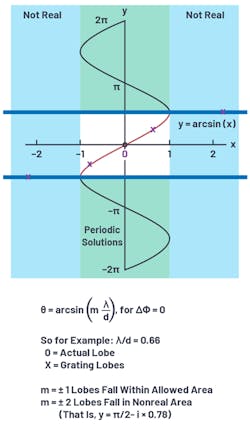
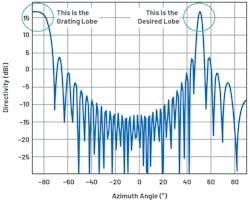
If we do so, then all of the spatial images (that is, m = ±1, ±2, etc.) will produce nonreal arcsin results, and we can ignore them. But if we can’t do this, and therefore some values of m > 0 produce real arcsin results, then we end up with multiple solutions: grating lobes (Fig. 2).
Grating Lobes for d > λ and λ = 0°
Here are some examples to better illustrate this scenario. First, consider the case at mechanical boresight where θ = 0, and therefore ∆Φ = 0. Then Equation 3 simplifies to Equation 5:
From this simplification, it’s evident that if λ/d is > 1, then only m = 0 could give an argument that’s bounded between –1 and +1. And that argument will just be 0, and the arcsin(0) = 0°, the mechanical boresight angle. So, this is all as we would expect. Furthermore, for any m ≥ 1, the arcsin argument will be too large (>1) and the resulting answer will not be real. We will see no grating lobes for θ = 0 and d < λ!
However, if d > λ (therefore, λ/d is <1), then multiple solutions—grating lobes—could exist. For example, if λ/d = 0.66 (that is, d = 1.5λ), then real arcsin solutions would exist for m = 0 and for m = ±1. That m = ±1 is the second solution, which is the spatial aliasing of the desired signal. Therefore, we can expect to see three main lobes, each with approximately equal amplitude, located at arcsin(0 × 0.66), arcsin(1 × 0.66), and arcsin(–1 × 0.66). In degrees, these angles are 0° and ±41.3°. In fact, this is what our array factor plot shows in Figure 3.
Grating Lobes for λ/2 < d < λ
In simplifying the grating-lobe equation (Equation 5), we chose to only look at mechanical boresight (∆Φ = 0). And we saw that, at mechanical boresight, grating lobes would not appear for d < λ. But from our analogy of sampling theory, we know that we should also expect to see some kind of grating lobe for any spacing greater than λ/2. So where are the grating lobes for λ/2 < d < λ?
First, recall how the phase changed with steering angle in Figure 4 from Part 1 of this article series. We saw ∆Φ range from 0 to ±π as the main lobe deviated from mechanical boresight. Therefore:
will range:
And for |m| ≥ 1, it will always be something beyond:
This restricts the minimum permissible λ/d if we want to keep the entire arcsin argument > 1 for all |m| ≥ 1. Consider two cases:
If λ/d ≥ 2 (that is, d ≤ λ/2), then you could never have multiple solutions, regardless of the value of m. All m > 0 solutions will result in an arcsin argument > 1. This is the only way to avoid grating lobes to the horizon.
But if we purposefully restricted ∆Φ to something less than ±π, then we could tolerate a smaller λ/d and still not see grating lobes. Reducing the range of ∆Φ means reducing the maximum steering angle of our array. It’s an interesting tradeoff that will be explored in the next section.
Element Spacing Considerations
Should the element spacing always be less than λ/2? Not necessarily! This becomes a tradeoff for the antenna designer to consider. If the beam is steered completely to the horizon, then θ = ±90°, and an element spacing of λ/2 is required (if no grating lobes are allowed in the visible hemisphere). But in practice, the maximum achievable steering angle is always less than 90°. This is due to the element factor and other degradations at large steering angles.
From the arcsin figure (Fig. 2, again), we can see that if the y axis, θ, is restricted to a reduced limit, then grating lobes only occur at scan angles that aren’t used anyway. What would this reduced limit (θmax) be for a given element spacing (dmax)? We had said previously that our goal is to keep:
We can use this to calculate where our first grating lobe (m = ±1) would appear. Making this change, and using Equation 1 from Part 1 for ∆Φ, gives:
Which simplifies to:
Then solving for dmax:
This dmax is the condition for no grating lobes in the reduced scan angle (θmax), where θmax is less than π/2 (90°). For example, if the signal frequency is 10 GHz and we need to steer ±50° without grating lobes, then, as Figure 4 shows, the maximum element spacing is:
Thus, restricting the maximum scan angle brings a freedom to extend the element spacing to increase the physical size per channel as well as extend the aperture for a given number of elements. An example application that could exploit this phenomenon is for an antenna assigned to a narrow, predefined direction. The element gain can be increased for directivity in the predefined direction; the element spacing also can be increased for a larger aperture. Both result in larger overall antenna gain within the narrowed beam angle.
Note that Equation 3 indicates a maximum spacing of one wavelength, even for zero steering angle. This is the case if grating lobes can’t be tolerated in the visible hemisphere. In the case of a GEO satellite, for example, the entire Earth is covered with a steering angle of 9° from mechanical boresight. It may be the case that grating lobes can be tolerated, if they don’t land on the Earth’s surface. In such a case, the element spacing may be several wavelengths, resulting in even more narrow beamwidths.
Also worth noting are antenna architectures that attempt to overcome the grating-lobe problem by producing a nonuniform element spacing. These are categorized as aperiodic arrays, with spiral arrays as an example. For mechanical antenna construction reasons, it may be desirable to have a common building block that can be scaled to a larger array, but this would produce a uniform array that’s subject to the grating-lobe conditions described.
Peter Delos is Technical Lead and Bob Broughton is Director of Engineering for Analog Devices’ Aerospace and Defense Group; Jon Kraft is Senior Staff Field Applications Engineer at Analog Devices.
>> Microwaves & RF Resources
.. >> Library: Article Series
.. .. >> Topic: Phased-Array Antenna Design
.. ... .. >> Phased-Array Antenna Patterns
References
Balanis, Constantine A. Antenna Theory: Analysis and Design, third edition. Wiley-Interscience, 2005.
Longbrake, Matthew. True Time Delay Beamsteering for Radar. 2012 IEEE National Aerospace and Electronics Conference (NAECON), IEEE, 2012.
Mailloux, Robert J. Phased Array Antenna Handbook, second edition. Artech House, 2005.
O’Donnell, Robert M. “Radar Systems Engineering: Introduction.” IEEE, June 2012.
Skolnik, Merrill. Radar Handbook, third edition. McGraw Hill, 2008.
About the Author
Peter Delos
Technical Lead, Aerospace and Defense Group, Analog Devices
Peter Delos is a technical lead in the Aerospace and Defense Group at Analog Devices in Greensboro, N.C. He received his BSEE from Virginia Tech in 1990 and MSEE from NJIT in 2004. Peter has over 25 years of industry experience, with most spent designing advanced RF/analog systems at the architecture level, PWB level, and IC level. He’s currently focused on miniaturizing high-performance receiver, waveform generator, and synthesizer designs for phased-array applications.