Algorithms to Antenna: Classifying Radar Micro-Doppler Signatures
In a previous blog, we described how moving targets introduce frequency shifts in radar returns due to the Doppler effect. We showed how you can model targets that are not rigid bodies and therefore have other vibrations and rotations beyond the “platform” motion. We also discussed how this micro-Doppler behavior can be simulated and analyzed.
In our most recent blog, we presented how you can use learning techniques in cognitive radar, software-defined radio, and efficient spectrum-management applications to identify modulation schemes. This month’s topic is focused on a combination of the two previous blog topics. We show how to classify pedestrians and bicyclists based on their micro-Doppler characteristics using a deep-learning network and time-frequency analysis.
This is a popular topic in automotive radar applications, where it’s important to understand when a pedestrian or bicyclist is in the road. It’s also a topic of active research in security applications.
Radar data collection in the field can be time-consuming. Data synthesis can help with generating large datasets. It can also aid in generating specific scenarios that may be difficult to recreate in the field.
Synthetic Data Generation
The movements of different parts of an object produce micro-Doppler signatures that can be used to help identify it. To illustrate this example, let’s focus on a pedestrian and a bicyclist. We use two modeling components: backscatterPedestrian and backscatterBicyclist from Phased Array System Toolbox. These functions simulate the radar backscattering of signals reflected from the objects. An example of the setup code for each is as follows:
The pedestrian model includes 16 body segments (left and right feet, left and right lower legs, left and right upper legs, left and right hip, left and right lower arms, left and right upper arms, left and right shoulders, neck, and head).
The bicyclist model includes the bicycle and its rider. The model accounts for the motion of the bicyclist and computes the sum of all reflected signals from multiple discrete scatterers on the bicyclist (>144 depending on the wheel size). The reflected signals are based on a multi-scatterer model developed from a 77-GHz radar system. Scatterers are located on five major bicyclist components (frame and rider, pedals, upper and lower legs, front wheel, and rear wheel).
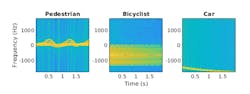
Using these modeling components, we generate thousands of pedestrian, bicyclist, and car radar echoes. Figure 2 shows a representative set of time-frequency maps for a pedestrian, bicyclist, and car.
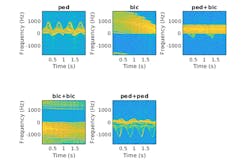
The normalized spectrograms show that the three objects have distinct signatures. Note how the spectrograms of the pedestrian and the bicyclist have rich micro-Doppler signatures caused by swinging arms and legs and the rotation of the wheels. By contrast, in this example, the car is modeled as a target with a rigid body and produces no micro-Doppler effects.
Classifying a single pedestrian or bicyclist is relatively simple, because the pedestrian and bicyclist micro-Doppler signatures are so different. The problem becomes much more challenging when we classify multiple overlapping pedestrians or bicyclists in the presence of Gaussian noise or car echoes.
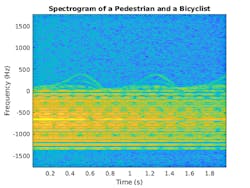
If multiple objects coexist in the radar field of view, the received radar signal is a summation of the detection signals from all of the objects. As an example, Figure 3 shows the micro-Doppler signature for a pedestrian and bicyclist with Gaussian background noise.
Because the pedestrian and bicyclist signatures overlap in time and frequency, differentiating between the two objects is difficult. This is where we will apply a classifier.
Radar Returns
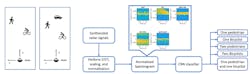
To do this, we train a convolutional neural network (CNN) by using synthesized radar returns from objects with varying properties—for instance, bicyclists pedaling at different speeds and pedestrians with different heights walking at different speeds. Other properties of the three objects are randomly tuned over a range of values; for example, pedestrians (height, heading, speed), bicyclist (heading, speed, gear transmission ratio), and cars (velocity). Another interesting point is that the bicyclist simulations include coasting, which significantly reduces the amount of micro-Doppler generated.
Radar returns reflect from different objects and different parts of objects. Depending on the configuration, some returns are much stronger than others. Stronger returns will obscure weaker ones.
Our dataset contains synthesized radar returns of the following scenes:
- One pedestrian
- One bicyclist
- One pedestrian and one bicyclist
- Two pedestrians
- Two bicyclists
As shown in Figure 4, one of the datasets is generated without car echo samples and the other includes car echo samples.
For the first dataset (without car echoes), the pedestrian and bicyclist signals are combined, Gaussian noise is added, and micro-Doppler signatures are computed to generate signatures for each of the five scenes to be classified. For the second dataset (with car echoes), the same process was used except that car echoes were added to half of the signatures.
Figure 5 shows the micro-Doppler signatures for all combinations of objects.
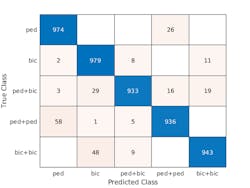
Figure 6 presents the confusion matrix for the classifier results when we train and classify the objects for the first dataset (no car echoes). The overall test accuracy is 0.9530 based on 1000 scenes for each category.
To understand the effects of car echoes, we classify the dataset containing car echoes with a network that was trained without car echoes. The prediction accuracy for the test dataset with the car echoes drops significantly, to around 70%, because the network never saw training samples containing car echoes. For this case, most of the prediction errors occur when the network takes in scenes from the “pedestrian,” “pedestrian+pedestrian,” or “pedestrian+bicyclist” classes and classifies them as “bicyclist.”
Car echoes significantly impede the performance of the classifier. To solve this problem, we retrained the CNN using data that contains car echoes. The prediction accuracy increases to about 87%.
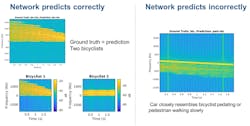
To better understand the performance of the network, we can focus on performance when classifying overlapping signatures. For example, without car echoes (left side of Fig. 7), we see two bicyclists with overlapping micro-Doppler signatures. The network correctly predicts that the scene has two bicyclists, even though from the plot, the signature appears to be from only one bicyclist.
The amplitudes of the Bicyclist 2 signature are much weaker than those of Bicyclist 1, and the signatures of the two bicyclists overlap. When they overlap, the two signatures can’t be visually distinguished. However, the neural network classifies the scene correctly.
As shown on the right side of Figure 7, the network confuses car echoes with a bicyclist. Here, the signature of the bicyclist is weak compared with that of the car, and the signature has spikes from the car echoes. Because the signature of the car closely resembles that of a bicyclist pedaling or a pedestrian walking at a low speed, and has little micro-Doppler effect, there’s a high possibility that the network will classify the scene incorrectly.
Simulating micro-Doppler returns can help you predict performance in radar systems. In an upcoming blog, we will look at how data collected with an Ancortek radar compares with simulation results.
To learn more about the topics covered in this blog, see the examples below or email me at [email protected]:
- Pedestrian and Bicyclist Classification Using Deep Learning (example): Learn to classify pedestrians and bicyclists based on their micro-Doppler characteristics using a deep-learning network and time-frequency analysis.
- Deep Learning Using Synthesized Data for Communications and Radar (white paper): Learn how to synthesize and label radar and communications waveforms, generate radar returns for moving objects, and train deep networks with synthetic data.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
About the Author
Rick Gentile
Product Manager, Phased Array System Toolbox and Signal Processing Toolbox
Rick Gentile is the product manager for Phased Array System Toolbox and Signal Processing Toolbox at MathWorks. Prior to joining MathWorks, Rick was a radar systems engineer at MITRE and MIT Lincoln Laboratory, where he worked on the development of several large radar systems. Rick also was a DSP applications engineer at Analog Devices, where he led embedded processor and system level architecture definitions for high performance signal processing systems used in a wide range of applications.
He received a BS in electrical and computer engineering from the University of Massachusetts, Amherst, and an MS in electrical and computer engineering from Northeastern University, where his focus areas of study included microwave engineering, communications, and signal processing.
Honglei Chen
Principal Engineer
Honglei Chen is a principal engineer at MathWorks where he leads the development of phased-array system simulation. He received his Bachelor of Science from Beijing Institute of Technology and his MS and PhD, both in electrical engineering, from the University of Massachusetts Dartmouth.