Algorithms to Antenna: Modeling Micro-Doppler Effects
We have described radar modeling in past blogs. Now, we want to dig a little deeper in terms of modeling objects and targets that a radar may see in its field of view. The most common technique is to define targets using radar cross-section (RCS) profiles that may vary with aspect angle, frequency, and fluctuations in motion.
Moving targets introduce frequency shifts in radar returns due to the Doppler effect. Targets that are not rigid bodies often have other vibrations and rotations in different parts beyond the platform movement.
For higher-fidelity target models, multiple scatterers can be used together to simulate additional motion, which is visible to a high-bandwidth radar. For example, they can detect motion such as a rotating blade or a pedestrian arm and leg swinging when crossing a street. The motion of these scatterers with respect to the platform motion will also result in micro-Doppler effects. These effects can add to the target “signature” and be used to help identify the object.
We are frequently asked about this topic, and one of the references we use faithfully was recently updated. The Micro-Doppler Effect in Radar, Second Edition, authored by Dr. Victor C. Chen, includes great new applications and examples. Dr. Chen is also the founder of Ancortek; you can find more micro-Doppler related material on his company website: www.ancortek.com.
We use this great reference to model micro-Doppler behavior. Below, we describe two applications that can be helped by micro-Doppler effects. First, we look at how micro-Doppler signatures are used to identify a pedestrian in an automotive radar return. In the second example, we use micro-Doppler signatures to determine the attributes of a helicopter blade.
Pedestrian Identification in Automotive Radar
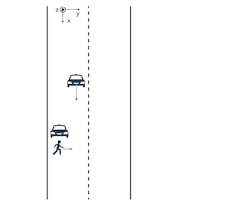
Let’s start with an ego vehicle equipped with a frequency-modulated-continuous-wave (FMCW) automotive radar system. The vehicle is traveling along a road with a car parked on the side of the street ahead. A pedestrian is walking out from behind the parked car (Fig. 1). This situation can be a challenge for the ego-vehicle radar to detect due to the difference in size between the parked vehicle and the pedestrian.
1. This drawing shows a pedestrian crossing a road from behind a parked car.
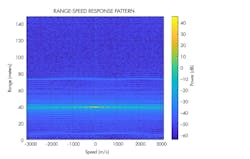
Figure 2 shows the range-Doppler map generated from the ego car’s radar. Because the parked car is a much stronger radar target than the pedestrian, the pedestrian is masked in the range-Doppler map. As a result, the map always shows a single object.
2. A range-Doppler map was generated for a parked vehicle with a pedestrian moving behind it.
Here, conventional range-Doppler processing will not help. But we can look to micro-Doppler effects in the time-frequency domain to help identify if there’s a pedestrian signature embedded in the radar signal.
In the spectrograms in Figure 3, the simulated signal (left side) contains only the pedestrian’s return, while the return on the right includes both the pedestrian and the parked car.
3. These spectrograms plot the micro-Doppler effects for pedestrian only (left) and pedestrian plus parked vehicle (right).
The swinging motion of arms and legs produces multiple parabolic curves in the time-frequency domain. These features can be used to determine whether a pedestrian is present in the radar’s field of view. One can see that the parked car’s return dominates the return—even in the time-frequency domain. The drop of the Doppler frequency is due to the ego car getting closer to the parked car. Here, the relative speed drops toward zero.
To see if there’s a return hidden behind the strong return, we can use singular value decomposition. Figure 4 shows the distribution of the singular value of the de-chirped pulses.
4. It’s possible to extract micro-Doppler return for a pedestrian when a parked vehicle is also present.
From the curve on the left side of Figure 4, it’s clear there are four regions in the singular value decomposition. Region A represents the most significant contribution to the signal, which is the parked car. Region D represents noise. Therefore, regions B and C are due to the mix of the parked-car return and the pedestrian return. Because the return from the pedestrian is much weaker than the return from the parked car, it can still be masked by the residue of the return from the parked car in region B. Therefore, we pick region C to reconstruct the signal, and then plot the time-frequency response again.
With the return from the car successfully filtered, the micro-Doppler signature from the pedestrian appears. The ego vehicle can then act accordingly to avoid an accident.
Estimating Blade Speed of a Helicopter
In the next example, consider a helicopter with four rotor blades. Figure 5 shows the scenario (left side) and the range-Doppler return from a short-range surveillance radar (right side).
5. Here’s a simulated range-Doppler response for a helicopter in motion.
Here, the helicopter is modeled by five scatterers: the rotation center and the tips of four blades. The rotation center moves with the helicopter body. Additional scatterers could be added to further increase the fidelity.
At each radar pulse, the helicopter moves along its trajectory. Meanwhile, the blades keep rotating, and the tips of the blades introduce additional displacement and angular speed.
The right side of Figure 5 shows the range-Doppler response using the first 128 pulses of the received signal. One can see the display of three returns at the target range of approximately 700 meters.
While the returns look as though they are from different targets, they are actually all from the same target. The center return, from the rotation center, is much stronger than the other two returns. This intensity is due to the reflection being stronger from the helicopter body when compared with the blade tips. The plot shows a speed of −40 m/s for the rotation center. This value matches the truth of the target radial speed.
The other two returns are from the tips of the blades when they approach or move away from the target at maximum speed. From the plot in Figure 5, the speeds corresponding to these two detections are about 75 m/s and −160 m/s.
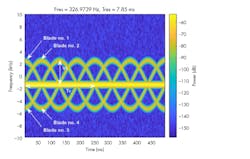
The time-frequency representation of micro-Doppler effects can reveal more information. Figure 6 shows the micro-Doppler modulation caused by blade tips around a constant Doppler shift. The image suggests that each blade tip introduces a sinusoid-like Doppler modulation. As illustrated, within each period of the sinusoid are three extra sinusoids appearing at equal distance. This appearance suggests that the helicopter is equipped with four equally spaced blades.
6. This is the simulated time-frequency representation of helicopter micro-Doppler effects.
In addition to the number of blades, the image also shows that the period of each sinusoid, Tr, is about 250 ms. This value means that a blade returns to its original position after 250 ms. In this case, the angular speed of the helicopter is about 4 revolutions per second, which matches the simulation parameter.
This image also shows the tip velocity, Vt, which can be derived from the maximum Doppler. The maximum Doppler is about 4 kHz away from the constant Doppler introduced by the bulk movement.
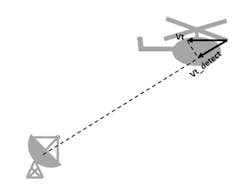
One can also obtain the correct maximum tip velocity, but the relative orientation must be considered (Fig. 7). Because the blades are spinning in a circle, the detection is not affected by the azimuth angle.
7. The relative orientation of the helicopter with respect to the radar is depicted.
Information such as number of blades, blade length, and blade rotation rate can help identify the model of the helicopter.
These types of examples help to introduce the basic concept of micro-Doppler effects and show their impact on the target return. They also show how to extract a micro-Doppler signature from the received I/Q signal and derive relevant target parameters from the micro-Doppler information. Simulation can be used to augment data you collect on SDR systems like those from Ancortek. They also help in algorithm development prior to deploying a system.
To learn more about the topics covered in this blog, see the links below or email me at [email protected].
- Introduction to Micro-Doppler Effects (example): Learn the basic concepts of micro-Doppler effects present in radar target returns.
- Doppler Estimation (example): Learn how pulsed radars can detect the radial velocity as derived from the Doppler shifts of moving targets.
- Range-Doppler Response (example): Learn how to visualize a signal as a function of range-Doppler.
- Overcoming SDR Design Challenges (resource kit): Learn how to overcome common software-defined radio design challenges by using model-based design with MATLAB.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
About the Author
Rick Gentile
Product Manager, Phased Array System Toolbox and Signal Processing Toolbox
Rick Gentile is the product manager for Phased Array System Toolbox and Signal Processing Toolbox at MathWorks. Prior to joining MathWorks, Rick was a radar systems engineer at MITRE and MIT Lincoln Laboratory, where he worked on the development of several large radar systems. Rick also was a DSP applications engineer at Analog Devices, where he led embedded processor and system level architecture definitions for high performance signal processing systems used in a wide range of applications.
He received a BS in electrical and computer engineering from the University of Massachusetts, Amherst, and an MS in electrical and computer engineering from Northeastern University, where his focus areas of study included microwave engineering, communications, and signal processing.
Honglei Chen
Principal Engineer
Honglei Chen is a principal engineer at MathWorks where he leads the development of phased-array system simulation. He received his Bachelor of Science from Beijing Institute of Technology and his MS and PhD, both in electrical engineering, from the University of Massachusetts Dartmouth.