Jump-Start Filter Design with Sophisticated Simulation Techniques
Download this article as a .PDF
Designing RF/microwave filters generally involves utilizing software tools to create simulation models. One factor that designers must be mindful of when modeling a filter is the amount of time needed for a simulation to execute. This length of time can be quite substantial in some cases.
Of course, when simulating a filter design, simulation data is acquired over a user-specified frequency range. Data is obtained across this frequency range at an interval that is also specified by the user. By decreasing the frequency interval, or step size, designers can essentially model filters more precisely. However, decreasing the step size generally comes at the expense of increasing the time needed for the simulation to execute.
One software company, COMSOL, has developed methods that can significantly reduce filter simulation time without sacrificing precision. With the RF Module, which is an add-on product to COMSOL Multiphysics software, designers can quickly simulate filters even when specifying a small step size.
This article explains how the Frequency-Domain Modal method within the RF Module software can accelerate filter simulation time. Two design examples are presented to illustrate how this method can benefit filter designers. The first design presented is a waveguide bandpass filter. A microstrip edge-coupled bandpass filter design is then analyzed. All simulations were performed with an Acer Aspire R14 R5-471T laptop, which has a 2.3-GHz Intel Core i5-6200U processor.
Waveguide Bandpass Filter Example
The first example presented is an iris-coupled waveguide bandpass filter with a center frequency of approximately 12.5 GHz. This filter has a WR-75 interface. Figure 1 shows the simulation model.
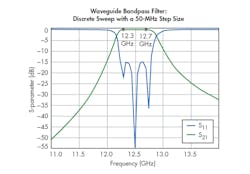
This waveguide filter was first simulated with the standard discrete sweep method. The frequency range of the simulation was 11 to 14 GHz. The step size was set to 50 MHz. Figure 2 shows the simulation results. Furthermore, the simulation time was approximately one minute, 20 seconds.
Figure 2 shows rough S-parameter plots—especially for S11. These results are due to the 50-MHz step size. Clearly, designers are likely to need smoother plots, which correlate to more precise modeling. Thus, a smaller step size is needed.
To acquire more precise data, the step size was then reduced to 1 MHz. The frequency range of 11 to 14 GHz remained the same. Simulating the filter with a 1-MHz step size produced the S-parameter plots shown in Fig. 3. Clearly, the 1-MHz step size produced much smoother plots in comparison to using a 50-MHz step size. However, the 1-MHz step size also increased the simulation time to almost one hour, demonstrating the tradeoff between precision and time.
To overcome the precision and time tradeoff, the Frequency-Domain Modal method can be utilized. With this method, filters can be simulated in a fraction of the time needed for a discrete sweep simulation to execute.
The Frequency-Domain Modal method involves an eigenfrequency analysis, which enables a structure’s resonance frequencies to be captured. The information from the analysis is used in the Frequency-Domain Modal study. The benefit of the Frequency-Domain Modal method is that it enables quick simulations of filters even when a small step size is specified.
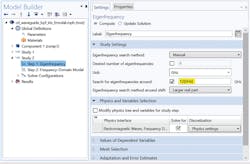
To demonstrate the Frequency-Domain Modal method, the waveguide bandpass filter was then simulated using this method. Figure 4 shows the software’s user interface when selecting the Frequency-Domain Modal study. One of the important parameters shown in Fig. 4 is “Search for eigenfrequencies around.” To obtain good results, this parameter should be set to a frequency value that is in the vicinity of the lowest passband frequency. Thus, 12 GHz was specified for this simulation.
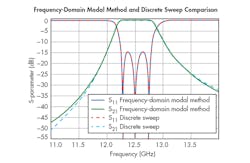
For the Frequency-Domain Modal simulation, the same 1-MHz step size was used. The frequency range of 11 to 14 GHz also remained the same. Figure 5 shows the results of this simulation along with the results of the previous discrete sweep simulation with a 1-MHz step size. The graph shows that the results from both simulations are very close. However, only a little more than one minute was needed for the Frequency-Domain Modal simulation to execute. These results therefore demonstrate the effectiveness of the Frequency-Domain Modal method.
In essence, one approach to design a filter such as this could be to first utilize the standard discrete sweep method with a larger step size in order to obtain preliminary results. The Frequency-Domain Modal method could then be used with a smaller step size to acquire more precise data. This approach could save valuable time in comparison to simply performing a discrete sweep simulation with a smaller step size.
Microstrip Edge-Coupled Bandpass Filter
The second design example is a microstrip edge-coupled bandpass filter. This filter has a passband from 9.7 to 10.2 GHz. It is designed on a 10-mil-thick Rogers RT/duroid 5880 laminate. Figure 6 shows the simulation model.
This filter was also first simulated with the standard discrete sweep method. The simulation was performed across a frequency range of 9 to 11 GHz. The step size was set to 50 MHz. Figure 7 shows the results of the simulation, which needed approximately 13 minutes to execute. Once again, the plots reveal a rough shape due to the 50-MHz step size.
The step size was then decreased to 5 MHz. The frequency range of 9 to 11 GHz remained the same. The simulation results are shown in Fig. 8. As expected, this simulation produced smoother plots. However, the simulation needed approximately two hours to complete.
The microstrip filter was then simulated using the Frequency-Domain Modal method. The step size remained at 5 MHz. The frequency range of 9 to 11 GHz also remained the same. Moreover, the “Search for eigenfrequencies around” parameter was specified at 9.5 GHz.
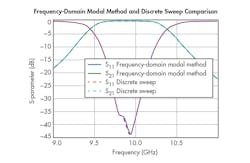
Figure 9 shows the results of the Frequency-Domain Modal simulation along with the previously shown results from the discrete sweep simulation with the same 5-MHz step size. As can be seen, the simulation results are practically identical. However, while the discrete sweep simulation needed approximately two hours to execute, the Frequency-Domain Modal simulation only needed approximately three minutes, 30 seconds. This analysis therefore further validates the Frequency-Domain Modal method.
In conclusion, this article demonstrated that the Frequency-Domain Modal method within the COMSOL Multiphysics software can benefit anyone involved with designing RF/microwave filters. The analysis validated that filter simulation time can be drastically reduced without having to sacrifice the precision that designers need. Those who are interested can also visit COMSOL’s Application Gallery, which contains various filter models. Step-by-step instructions are provided to explain the process of building a model.