Design Parameters for a Wideband, Second-Harmonic Gunn Oscillator

What you’ll learn:

• Understanding the operating principles of a Gunn diode.
• Waveguide techniques for Gunn oscillator design.
• Key starting parameters for dual-tuned microwave Gunn oscillators.

Despite being an older, established technology, demand continues for wideband high-frequency oscillators based on the venerable Gunn diode. Sadly, designing and building such oscillators is a skill that seems to be waning these days.

Today’s younger engineers turn increasingly to newer technologies when designing oscillators. In addition, they rely more on analog simulation tools to iron out the intricacies of the circuits. Meanwhile, older engineers who might have previous experience working with Gunn diodes are in the twilight of their careers, putting at risk the retention of their knowledge for the industry at large.

The Gunn diode has hung around since its invention by J.B. Gunn in the early 1960s, and for good reasons. Even though it’s referred to as a “diode” because it has an anode and a cathode, it’s technically not a diode because it doesn’t have a conventional PN junction. Rather, it’s composed of a single N-type semiconductor, which is why it’s known as a transferred-electron device (TED).

A traditional PN-junction diode can perform rectification, which isn’t the case with a Gunn diode since it conducts in both directions. But because its two terminals, both with negative dynamic resistance, can produce extremely high switching speeds, the Gunn diode lends itself to wideband oscillators for applications such as radar systems and sensors, communications, radiometric systems, and more. These days, Gunn diodes are typically fabricated in gallium arsenide (GaAs) with operating frequencies up to 200 GHz and gallium nitride (GaN) in frequencies of up to 3 THz.

There’s a plethora of information and articles relating to Gunn-diode-based oscillators. Two notable articles offering useful insights are by W.H. Haydl¹ and J.E. Carlstrom². The wideband oscillator stems from the initial work carried out by Haydl, which Carlstrom subsequently took further. Another good source of information is E.L. Holzman and R.S. Robertson’s book.³ “Solid-State Microwave Power Oscillator Design.” 

In this brief article, we aim to provide some guidance on considering the fundamental design parameters for such a wideband, second-harmonic Gunn oscillator.

Design Considerations for Gunn-Diode-Based Oscillators

Let’s consider the case of an E-band, mechanically tuned Gunn oscillator. For a waveguide, we’ll go with a standard WR12 waveguide that has dimensions of 3.10 × 1.55 mm. For the circuit itself, we’ll use a reduced height of 0.775 mm, which will taper out to full height.

The cutoff frequency for a WR12 waveguide is λ_c = 48.39 GHz. The cutoff frequency is a key parameter, because any waves at lower frequencies will not propagate. The circuit exploits this fact by using fundamental Gunn devices, which are more readily available on the commercial market.

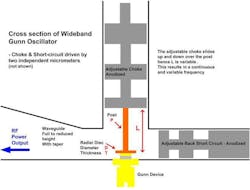
Figure 1 shows a cross section of the mechanically dual-tuned Gunn oscillator. The Gunn diode is mounted into the base of the WR12 waveguide’s cavity section with a taper to full height. The location of the Gunn diode also forms a coaxial cavity with an adjustable length.

While this coaxial cavity supports the fundamental-frequency mode of operation, only the harmonic frequency is allowed to propagate via the waveguide section (i.e., the cutoff frequency). Thus, by altering the length of the coaxial cavity, the fundamental frequency can be altered—hence, the output second-harmonic frequency.

Power is coupled out of the circuit by using the radial impedance transformer and adjusting the phase within the waveguide channel, which is accomplished by a short circuit located in the reduced height section. Because the radial impedance transformer isn’t broadband, power will be optimum for smaller bandwidths. The dimension of the radial disc is typically half of the waveguide’s length.

Parameters that have secondary effect on the oscillator performance are:

• Radial disc thickness (T)
• Post diameter (P)

The mechanism for broadband tuning is adjustment of the length, L, of a coaxial cavity (Fig. 1, again). Varying the cavity’s length produces very large bandwidths. Near-full bandwidth is achievable with careful attention.

We have generated a model for prediction behavior of these dual-tuned microwave Gunn oscillators.  The power output power is less predictable and usually dictated by the Gunn device in use.

The initial key parameters are as follows:

• Disc diameter (D) ~ 2.45 mm for 78-GHz operation, which is half the length of the WR12 waveguide
• Disc thickness (T) ~ 0.25 mm
• Post diameter (P) ~ 0.6 mm

Measured Data for Gunn-Diode-Based Oscillators

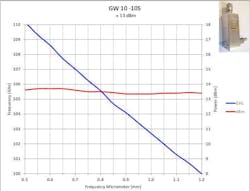
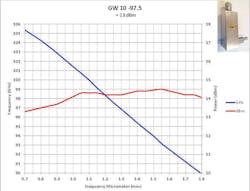
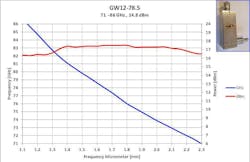
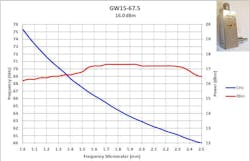
Figures 2 and 3 present typical measured data for a WR10 waveguide for bandwidths with useful power > +10 dBm. In addition, data is shown for E- and V-band units in Figures 4 and 5.

For the E-band case discussed in this article, Figure 6 provides the predicted frequency behavior. There’s good correlation between measured and predicted frequencies, which renders the modeling useful. And for repeatability, micrometers are fitted for both cavity frequency adjustment and power optimization as shown in Figure 7.

In summary, wideband, mechanically tuned Gunn oscillators can be produced to cover significant parts of the microwave spectrum. Multiple units will cover a particular waveguide with useful output power (e.g., > +10 dBm). Such oscillators offer a compact and reliable solution for high-frequency applications at a relatively lower cost when compared with upconversion or multiplier/synthesizer-based solutions.

References

1. W.H. Haydl. “Harmonic Operation of GaAs Millimeter-Wave Transferred-Electron Oscillators.” Electronics Letters, Volume 17, Issue 22, October 1981.

2. J.E. Carlstrom, R.L. Plambeck, D.D. Thornton. “A Continuously Tunable 65-115-GHz Gunn Oscillator.” IEEE Transactions on Microwave Theory and Techniques, Volume 33, No. 7, July 1985.

3. E.L. Holzman and R.S. Robertson. “Solid-State Microwave Power Oscillator Design.” Artech House, Norwood, MA, 1992.