Simulation Domain Transformation Between Time and Frequency
Download this article in PDF format.
The momentum for realizing the 5G network has reached a fever pitch, with many of the major wireless providers touting the proposed launch of the network. However, one question remains: “What still needs to be done to make this a reality?” System and device design engineers working on the frontlines of 5G, the Internet of Things (IoT), and millimeter-wave (mmWave) communications can benefit from electromagnetic (EM) simulations with a cost-effective procedure. Simulation offers a virtual test environment that ultimately reduces the duration of the design cycle.
Conventional EM numerical analyses, such as finite-element method (FEM) and method of moments (MoM), are typically performed in the frequency domain for S-parameter calculations. S-parameters provide information like impedance mismatch, insertion loss, and phase variation as a function of frequency. This type of analysis is compatible with typical network-analyzer measurements conducted in the laboratory.
The simulation analysis can also be examined in the time domain for the purposes of time-domain reflectometry (TDR). With TDR data as a function of time, it’s possible to identify the abnormal area on a circuit where the performance of a device has diminished due to a signal discontinuity and impedance mismatch.
Contrary to the methods mentioned above, the finite-difference-time-domain (FDTD) method is studied in the time domain. However, S-parameters and the antenna radiation pattern are presented in the frequency domain through the Fourier transform. The Fourier transform makes it possible to convert the simulated results from one domain, such as frequency, to another domain, such as time. This provides designers with more information so that they can make informed decisions concerning device designs.
EM Physics Interfaces and Fourier Transform
When using FEM to analyze high-frequency EM problems, we often prioritize investigating the S-parameters in the frequency domain. Using a fast Fourier transform (FFT) process, we are able to convert the data between the frequency domain and time domain.
The RF Module, a high-frequency EM simulation add-on tool that’s available in COMSOL Multiphysics software, provides a series of useful physics interfaces to conduct such analysis. They include:
- Electromagnetic Waves, Frequency Domain (frequency-domain finite element method, FDFEM)
- Electromagnetic Waves, Transient (time-domain finite element method, TDFEM)
- Electromagnetic Waves, Time Explicit, (time-domain discontinuous Galerkin method, DG)
- Transmission Line (frequency-domain transmission-line equation)
Those physics interfaces play the expected role of computing traditionally domain-specific results. They can also be extended to extract more information beyond the original computational domain. After finishing the simulation with Electromagnetic Waves, Frequency Domain, the results include traditional S-parameters, near electric- and magnetic-field distribution, and far-field norm radiation patterns. If the bandwidth of the frequency sweep in a simulation is wide enough, performing frequency-to-time Fourier transform on the dependent variable of the governing equation will lead to the frequency-dependent solutions being converted to time-dependent information (Fig. 1).
1. TDR analysis shows the impact on the signal quality due to the various via and anti-via sizes.
The Electromagnetic Waves, Transient TDFEM physics interface is more suited for problems with nonlinear material properties, or for signal-path discontinuity analysis like time-domain reflectometry. When the time step used in the simulation is fine enough, the time-dependent solutions can be converted to frequency-dependent S-parameters in a very wide bandwidth by time-to-frequency Fourier transform.
TDR Analysis from Frequency Domain with Frequency-to-Time FFT
While the main focus of the frequency-domain simulation involves computing S-parameters to study the performance of devices, it can be inspected in the time domain as well. After this conventional frequency-domain simulation is conducted, using the frequency-to-time FFT provides the impulse response for the input signal. Since it’s not a static case, the frequency-domain simulation may not include the result at dc. The FFT outcome is a time-domain bandpass impulse response of the device.
The characteristics of the frequency data that are used to input the frequency-to-time FFT define the quality of the time-domain outcome. If the starting frequency is not low enough, the FFT results may develop a visible low-frequency envelope noise. Alternatively, if the bandwidth is not wide enough, the resolution of the time-domain signal output will not appear sharp and clear in the simulation results.
The frequency step defines the alias period and location in the time domain. After performing the FFT, the signal fluctuations in the time domain show where the discontinuities lie on the signal path (Fig. 2).
2. The voltage fluctuation at the excitation lumped port gives the round-trip time of a signal to the discontinuities. It’s possible to detect potentially defective parts of a transmission line using a TDR plot.
The frequency-domain study in this model is performed from 1 MHz to 30 GHz. The initial results are converted to the time domain. The simulation results demonstrate the lumped-port voltage. Several overshoots and undershoots are also observed. The location of the physical discontinuities that cause undesirable impedance mismatches can be spotted by identifying material properties for the phase-velocity calculation and determining the round-trip travel time of the input signal from the port to a location where one can pinpoint the signal fluctuation.
Wideband S-Parameters and Far-Field Radiation Pattern from Time Domain with Time-to-Frequency FFT
The signal responses of circuits and antennas in a very wide band along with a fine frequency step can be achieved by running a one-shot time-domain simulation and converting the results to the frequency domain via time-to-frequency FFT. This type of conversion requires a modulated Gaussian input energy to excite the device being simulated and a sampling rate defined by the time-step to fulfill the Nyquist criterion (Fig. 3).
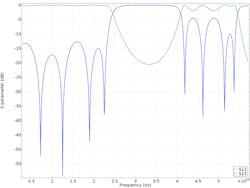
3. This is a coaxial bandpass filter model. It’s simulated in the time domain, but the results are presented in the frequency domain.
The modulated Gaussian pulse in the time domain can be viewed as a Gaussian pulse shifted to the modulation center frequency in the frequency domain. The simulation results demonstrate that the computed S-parameters are distributed around the modulation center frequency, f0, with the bandwidth 2f0. The resolution of the results in the frequency domain is determined by the maximum time of the input time-domain signal.
With the modulated Gaussian pulse, the energy level in the circuit decays as time passes until it eventually reaches close to zero level. To provide a long-time input signal, the simulation need not be performed for the length of time. As soon as the energy level in a specific probing domain is attenuated enough, the simulation can be stopped, and the remaining time can be filled with zeros. Using this zero-padding technique, it’s not necessary to sacrifice a long time of operation to obtain a fine frequency resolution (Fig. 4).
4. Shown are wideband S-parameters of a coaxial bandpass filter after FFT. The modulation center frequency is 30 GHz.
The energy level of the area, such as the beginning and end of the Gaussian pulse, is relatively low. In turn, the quality of the signal is vulnerable to the numerical noise. The outcome of the FFT can be filtered to truncate these ranges next to 0 and 2f0 Hz to enhance the data quality.
Wideband antenna far-field radiation patterns are also useful results of the time-to-frequency FFT process. The related antenna postprocessing variables like antenna gain and realized gain are properly scaled based on the input power levels proportional to the Gaussian pulse (Fig. 5).
5. The 3D antenna gain pattern in a dB scale is plotted for a printed dual-band strip antenna, with the norm of electric field on the antenna board at 2.25 GHz.
Simulation Techniques Enhancing the Modeling Capability
In reality, it may appear that computational resources are quite limited in addressing 5G and mmWave communications due to the increasing size of the analysis. It’s inevitable to experience the limitation of the resources and the time needed to find a simple and efficient way to set up the physics with relevant computational representation. The Fourier transform technique described with examples here won't be the ultimate solution for all modeling issues, but it will offer an alternative method to detour the obstacles associated with enhanced postprocessing studies.
Jiyoun Munn is RF Technical Product Manager at COMSOL.
About the Author
Jiyoun Munn
Technical Product Manager, COMSOL Inc.
Jiyoun Munn is the technical product manager for the RF Module at COMSOL, and a senior member of IEEE. He has two decades of experience in the RF industry, developing over 150 antenna and microwave device prototypes. Munn also holds patents for antenna interrogation systems. He received his MS degree in electrical engineering from the University of Michigan.