This file type includes high resolution graphics and schematics.
Magnetic-resonance-imaging (MRI) techniques offer powerful techniques for studying the inside of the human body, but the engineering involved in these systems is quite complex. MRI systems require high-power fields across a range of frequencies from static to megahertz; interactions between the electromagnetic (EM) fields and the human body further complicate MRI system design. Safe, reliable MRI systems call for RF coils capable of homogeneous fields with low specific absorption rate (SAR), but measuring fields inside the body is not practical. This report describes a workflow for using computer-aided-engineering (CAE) simulation to model the behavior of these high-power coils in a realistic therapeutic environment, including the use of accurate voxel models, bioheat solvers, and a specialized spin-ensemble simulator. Simulation results will be compared where possible to measurements from phantoms and human subjects.
Related Articles
• Resonators Support UHF MRI Systems
• Picking A Suitable CAE Software Package
• Medical Applications Seek Wireless Solutions
Safety and efficiency are important when designing any MRI device. During an MRI scan, the patient is subjected to significant energy from RF fields, typically at frequencies on the order of tens or hundreds of megahertz. These fields deposit energy in the body, which results in heating. If the temperature rises too much, significant tissue damage can occur.
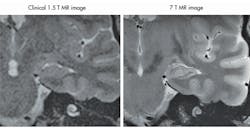
The new generation of ultra-high-field devices, with B-fields of 7 T, 9.4 T, or higher, introduces a new set of problems for MRI designers to consider. High-field devices produce images with much better resolutions than their low-field counterparts (Fig. 1).1 But they also operate at higher frequencies and produce higher power absorption in the human body; while the signal-to-noise ratio (SNR) improves linearly over frequency, the SAR is proportional to the square of the frequency, and this can increase heating effects substantially.
1. This is a comparison of the images from low- and high-field MRI systems, showing a cross-section of a hippocampus.
Higher frequencies also represent shorter wavelengths: For a typical 7-T device, these will be around 13 cm, comparable to the size of structures in the body. For such short wavelengths, interference has a major effect on the quality of the images. Figure 2 shows a possible result of such interference, with a large shadow obscuring the view of the brain. These shadows can hide clinically relevant details, so it is important that these be reduced as much as possible.
2. This is an MRI scan degraded by interference.
To reduce interference and improve patient safety, while still experiencing the benefits of high-field MRI, radiographers use multichannel coils that allow very precise control of the RF fields. Computer simulation can be used to calibrate these coils to prevent crosstalk between separate parts of the coil, and to ensure that the coils produce homogeneous fields in the area of interest. Simulation offers a faster and less expensive means of checking a design than repeatedly fabricating and testing prototype coils and making incremental changes in each generation and can also provide additional insight into the functional mechanisms of a system, allowing automatic optimization and tuning schemes.
This file type includes high resolution graphics and schematics.
Simulation Gameplan
This file type includes high resolution graphics and schematics.
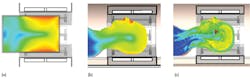
Heating and energy absorption are difficult to test experimentally, except in simplified phantoms such as homogeneous models filled with fluid. Because these phantoms are so simple, the energy absorption experienced by a phantom may have little relation to the energy absorbed by an actual person, as the body reflects and focuses the RF fields in hard-to-predict ways, as shown by Fig. 3.2 These effects can be thoroughly investigated by simulating realistic heterogeneous models, based on the electromagnetic properties of human tissue.
3. These simulated images of (a) a cylindrical phantom, (b) a homogeneous head phantom, and (c) a heterogeneous head model are from the Virtual Family (ref. 2), calculated in the CST MICROWAVE STUDIO® simulation software.
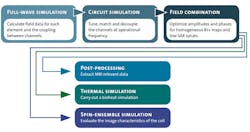
Both time- and frequency-domain solvers can be used to simulate RF coils. When human body models are included, however, time-domain methods represent the more practical approach. Figure 4 shows the workflow for tuning and simulating a head coil.3 The first step, simulating each port of the coil in turn, is the most computationally intensive step of the process. However, it only needs to be carried out once. The simulation generates field data and an S-parameter matrix, describing how RF energy propagates through the multiport network.
4. This block diagram represents the simulation workflow for a typical multiple-channel coil.
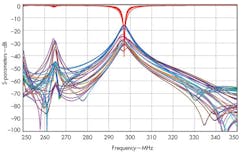
The coil can then be connected to a tuning circuit (Fig. 5), using a circuit simulator such as CST DESIGN STUDIO™ from Computer Simulation Technology. The software uses S-parameters to tune the circuit elements around the coil without having to run the full-wave simulation again. This produces one tuned and matched field per channel (Fig. 6). The fields from each transmitter can then be combined and, by optimizing the phase and amplitude at each port, the combined field can be made homogeneous in the area of interest.
5. This is the tuning circuit for a head coil simulated in the CST DESIGN STUDIO™.
6. These S-parameters for a tuned coil show good coupling at the desired frequency of 297.2 MHz.
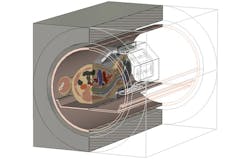
Simulating an empty coil will not provide a full picture of how it will work in practice, however. As mentioned previously, placing a patient in the machine loads the coil and introduces sources of interference, which will affect the EM field distribution. To ensure that the coil produces a homogeneous field inside the subject, the optimizer can also be run with a model inside the coil (Fig. 7), to find a usable field that takes into account the EM properties of the body.
7. This diagram shows a HUGO voxel model being simulated within a head coil.
Once a homogeneous field has been produced, whether with a single-channel or multiple-channel coil, and the results have been verified, the field must be evaluated to remain within the safety guidelines set by the International Electrotechnical Committee (IEC) and standard IEC 60601-2-33. Because it is difficult to determine the temperature distribution inside a patient, the standard way of quantifying MRI safety is by means of the SAR. The SAR is the power absorbed by the body per mass of tissue. There are a number of ways of presenting SAR: averaged over a volume, over a whole organ or structure, or simply as a point-by-point value. There are various legal SAR limits to prevent patients from being exposed to too much RF power during an MRI scan. Post-processing methods can calculate various types of SAR automatically for both standard and worst-case tuning instances, along with other relevant quantities such as the B1+ (transmit) field and the power loss.
The best practice for calibrating a coil is to run simulations using a number of voxel models, evaluate the field distribution and SAR for each one, then find the most critical type of SAR for each model. For example, if the worst-case SAR includes a small but severe hotspot, the point SAR or 10-g average SAR is the most critical one to reduce. If the power loss is evenly distributed across a large area, the SAR averaged across the whole body or a part of it is more likely to be important. If the scan region includes a particularly sensitive organ, the SAR across particular tissue types can be calculated as well to determine how much energy that organ will absorb. Once a designer knows which SAR values are most critical, efforts can be made to reduce those values. Since absorbed power scales linearly with the power of the coil, it’s relatively simple to decrease the power of the coil until all SAR values are within the safe region.
This file type includes high resolution graphics and schematics.
SAR Strategy
This file type includes high resolution graphics and schematics.
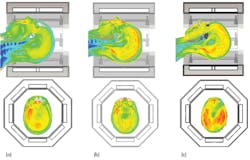
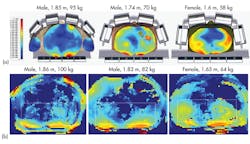
Figure 8 provides an example with three different models exposed to the same field from a head coil. In the models shown in Figs. 8(a) and (b), the SAR distributions are quite uneven, with some noticeable hotspots. In these images, the most critical SAR value is the 10 g averaged SAR, and the maximum permissible average power is 25 W for the model in Fig. 8(a) and 33 W for the model in Fig. 8(b). In the model in Fig. 8(c), the SAR distribution is very different. There are no hotspots: the power loss throughout the imaging region is fairly constant. In this case, both the SAR averaged across the entire head and the 10 g averaged SAR are more important, and the maximum permissible average power is 35 W.
8. These images show SAR distributions in three different voxel models in the same head coil, in transverse (top) and sagittal (bottom) planes.
Based on these results, the coil’s average power over the cycle should be kept below 25 W, the lowest of the permissible power values. At this level, it is unlikely that the coil will ever produce enough RF power to harm a patient. But it also means that the image quality may be reduced or the duration needed to take the image may increase. The use of CAE simulation can help to determine the maximum permissible field input power for different patients, so that every scan can produce a good quality image without exposing the patient to unnecessarily high RF fields.
SAR was originally introduced as a way to estimate heating within the body from RF fields, without taking into account the complex thermal properties of living tissues. Cells generate heat, while blood flow disperses temperature hotspots and sweating promotes heat loss through the skin. As Fig. 9 shows, a phantom cannot replicate these so-called “bioheat” effects, and it is impractical to measure the temperature distribution within a living patient undergoing an MRI scan. It is often more appropriate to use a bioheat solver to calculate temperature distributions inside the human body. A tissue temperature to +39°C is generally considered acceptable. Practical experience shows that temperature is typically a less critical criterion than SAR, so more power can be applied to an MRI coil while still maintaining patient safety.
9. These images show simulated temperature distributions for a homogeneous phantom (left) and a heterogeneous model (right), taking bioheat into account.
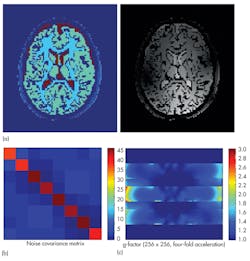
If it is not possible to achieve a perfect EM field distribution, it can be useful to evaluate the impact of an inhomogeneous EM field on the final image, and if compensation can be provided by the MRI sequence. Such compensation may require a dedicated MRI simulator such as the Juelich Extensible MRI simulator (JEMRIS).4 MRI simulators solve the Bloch equation, which describes the behavior of spins exposed to magnetic fields in a macroscopic way. In this way, MRI imaging can be simulated and relevant quantities such as a coil’s field of view (FOV), its g-factor for parallel imaging, and the noise covariance between the different channels can be calculated (Fig. 10). Integration between EM, thermal, and spin simulations provides a complete MRI simulation workflow. Of course, a simulation is only useful if it can be applied to the real world. Once a prototype of a coil has been constructed, it can be compared to actual measurements for that design. Homogeneous phantoms are widely available in MRI labs and easy to test, and their simple structure makes them simple to simulate, as well.
10. These images are outputs from JEMRIS for an eight-channel head coil, showing (a) full simulated MR images of the brain, (b) the coupling between each coil, and (c) its g-factor across a transverse slice.
This file type includes high resolution graphics and schematics.
Final Conclusions
This file type includes high resolution graphics and schematics.
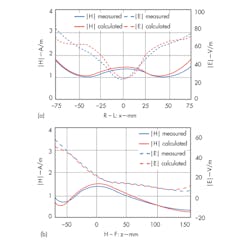
Figure 11 shows an experimental setup for evaluating a field distribution inside a head coil. A cylindrical phantom filled with tissue simulation fluid was used, and a model with the same EM properties was constructed in CST MICROWAVE STUDIO (MWS) simulation software from CST. The phantom was exposed to a field from the head coil, and the magnitude of the electric and magnetic fields within the phantom was measured. Measured results (Fig. 12) are close quantitatively to the simulated values.5
11. These images show a simulated phantom in (a) a head coil and (b) a real phantom.
12. These plots represent s show H- and E-field distributions along (a) the x (left-right) and (b) z (superior-inferior) axes of a phantom.
Related Articles
• Resonators Support UHF MRI Systems
• Picking A Suitable CAE Software Package
• Medical Applications Seek Wireless Solutions
Measurements can also be used to test the applicability of different voxel models. Most patients will not be perfect matches to voxel models, but much can be learned from comparisons between simulations and experiments. Using three different body models, a body coil was simulated, and three subjects similar in body shape to the models in the simulations were found and scanned. Figure 13 shows that the B1+ field distribution measured for an applied field agree closely with simulations. Although the models were not exact matches for patients, they were useful in predicting key features of the EM field, such as which fields would be homogeneous and which would not.
13. The images show (a) simulated field distributions in three patients from identical applied fields from a body coil and (b) measured field distributions in three similar subjects.
At present, these simulations are still most useful at the design stage of an MRI coil, to ensure that the coil will produce usable images from a wide range of body shapes. But it is hoped that the simulations may one day lead to look-up tables for improved MRI scanning performance, allowing radiographers to use the results from simulations to calibrate and adjust their coils without time-consuming prescans, as well as matching and tuning procedures.
Andreas Bitz, Senior Scientist
Erwin L. Hahn Institute for Magnetic Resonance Imaging, Arendahls Wiese 199, Tor 3, D-45141 Essen, Germany; (+49) 201-183-6070, FAX: (+49) 201-183-6073.
Jorg Felder, RF Engineer
Forschungszentrum Julich GmbH, 52425 Julich, Germany; (+49) 2461-61-0, FAX: (+49) 2461-61-8100.
Tilmann Wittig, Principal Engineer and Bio-EM Market Coordinator
Computer Simulation Technology (CST), Bad Nauheimer Strausse 19, 64289 Darmstadt, Germany; (+49) 6151-7303-0.
References
1. J.M. Theysohn, O. Kraff, S. Maderwald, M.U. Schlamann, A. de Greiff, M. Forsting, S.C. Ladd, M.E. Ladd, and E.R. Gizewski, “The Human Hippocampus at 7 T—In Vivo MRI,” Hippocampus, Vol. 19, 2009, pp. 1-7.
2. A. Christ, W. Kainz, E.G. Hahn, K. Honegger, M. Zefferer, E. Neufeld, W. Rascher, R. Janka, W. Bautz, J. Chen, B. Kiefer, P. Schmitt, H.P. Hollenbach, J. Shen, M. Oberle, D. Szczerba, A. Kam, J.W. Guag, and N. Kuster, “The Virtual Family - development of surface-based anatomical models of two adults and two children for dosimetric simulations,” Physical Medicine Biology Vol. 55, 2010, pp. N23-38.
3. S. Orzada, O. Kraff, L.C. Schäfer, I. Brote, A. Bahr, T. Bolz, S. Maderwald, M.E. Ladd, and A.K. Bitz, “8-Channel Transmit/receive Head Coil for 7 T Human Imaging Using Intrinsically Decoupled Strip Line Elements with Meanders,” Proceedings of the International Society of Magnetic Resonance Medicine (ISMRM), Vol. 17, April 2009, p. 3010.
4. T. Stöcker, K. Vahedipour, D. Pflugfelder, and N. J. Shah, “High Performance Computing MRI Simulations”, Magnetic Resonance Medicine, Vol. 64, 2010, pp. 186-193.
5. A.K. Bitz, O. Kraff, S. Orzada, S. Maderwald, I. Brote, S. Johst, and M. E. Ladd, “Assessment of RF Safety of Transmit Coils at 7 Tesla by Experimental and Numerical Procedures,” Proceedings of the International Society of Magnetic Resonance Medicine(ISMRM), Vol. 19, May 2011, p. 490.
This file type includes high resolution graphics and schematics.