Download this article in PDF format.
The impending 5G network has created a race for new spectrum bands to accommodate wireless traffic. As smartphone technology continues to offer more complex solutions, the need to transmit and receive paths from a variety of sources requires multiple bands operating simultaneously through a single antenna or multiple-input, multiple-output (MIMO) systems.
Microwave cavity filters are utilized to get rid of unwanted frequency components. They are found in telecommunication infrastructures that handle signals ranging from tens of megahertz to several gigahertz.
A filter’s performance may vary under severe environmental conditions. For example, a drastic rise in temperature can result in structural deformation caused by unexpected heat expansion. The physical phenomena beyond electromagnetics (EM) may not be included in a conventional EM simulation, as well as indoor laboratory measurements, despite having a large impact on the final product.
Resonance Frequency Changes Due to Thermal Drift
When a cavity filter is built with metallic materials, its performance in terms of resonant frequency can be vulnerable to severe temperature fluctuations. High-power loads or harsh environmental conditions can result in thermal drift, which makes it difficult to stabilize the high frequency of the filter. However, with the help of multiphysics simulation, it can be easy to analyze the resonant frequencies of an arbitrary shape of a structure through an eigenfrequency study.
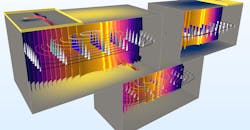
1. This is a slice plot of electric field norm and surface plot of surface current density norm.
Consider an example model of a cavity filter that consists of a thin metallic box that’s finished with copper and contains a cylindrical post (Fig. 1). The simulation was conducted to determine the effect on the filter resonance when the temperature changes from 0 to +100°C. Three things we are interested in analyzing include:
- Structural mechanics
- Geometry deformation
- EM waves
These parameters capture how the temperature increase affects structural deformation and the cavity filter’s resonant frequency. We found that the thermal expansion and associated drift in eigenfrequency are caused by a uniform increase in the temperature of the cavity wall and the post surface (Fig. 2). Thermal drift has become a bigger concern as the frequency spectrum becomes more crowded in the race for 5G. Engineers designing cavity filters in locations that are subject to extreme conditions will want to be sure they conduct this type of analysis.
2. Here’s a surface plot of total displacement due to the thermal expansion. The displacement plot is exaggerated for visualization purposes.
Materials Make a Big Difference
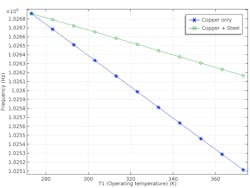
Let’s now look at an example made of steel iron. By adding a material with a lower thermal expansion coefficient, such as steel iron, we are able to reduce the variation of the resonant frequency caused by the temperature increases. To examine the differences between the first example, containing copper only, and this second example that contains copper and steel, we conducted another eigenfrequency analysis using multiphysics simulation (Fig. 3).
3. These plots show eigenfrequency as a function of temperature.
We found that the reduced thermal expansion of the tuning post results in a lower capacitive coupling between the top surface of the post and the cavity, which impacts the stability of the resonance frequency. The key performance metrics for filters include minimal loss for the desired signals and adequate removal of undesired interference. Using simulation to determine the optimal combination of materials based on the environmental conditions where your cavity filter will be housed will enable a successful design.
S-parameter Study of Tunable Cavity Filter Using Piezoelectric Actuator
In general, the resonant frequency of filter devices is a function of the electrical size of the cavity structure. By tweaking the physical shape of a structure, its corresponding resonance can be tuned. The adjusted amount of reactance, such as capacitive coupling inside of a cavity, may contribute to the lower resonant frequency obtained from a hollow cavity that’s limited by electrical length.
The metallized rectangular post in the center of the cavity is not connected to the ceiling of the structure, leaving a thin gap that induces a strong capacitive coupling. The capacitance is stronger and more sensitive to the gap size variation when the gap is thinner.
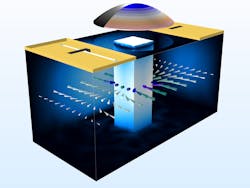
4. Shown here is surface plot of electric field norm on the cavity walls, contour plot of piezoelectric actuator displacement, and arrow plot of electric field in the middle of the cavity at 3.05 GHz with a dc bias of −300 V. The displacement plot is exaggerated for visualization purposes.
To take advantage of this observation, we looked at deploying a circular disk made of a piezoelectric actuator on top of the cavity, right above the metallic post (Fig. 4). The piezoelectric actuator is deformed by dc bias and controls the induced capacitive coupling between the top surface of the post and the bottom of the piezoelectric disk. The filter’s frequency response is tunable with the value of dc bias that generates different shape patterns of structural deformation.
The EM wave resonance behavior is affected by multiple physics phenomena. The deformation of the piezoelectric actuator with variable dc bias are numerically described in this model (Fig. 5). These effects can be numerically examined through the following physics:
- Solid mechanics
- Electrostatics
- EM waves
- Moving mesh
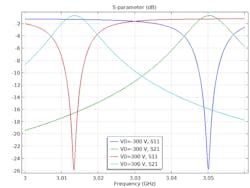
5. These S-parameter plots describe the resonant frequency change due to the different dc bias voltages applied on the piezoelectric actuator.
The combination of solid mechanics and electrostatics describes how the piezoelectric actuator is mechanically deformed by a varying external electric potential. Within the same simulation environment, we evaluated the EM resonances by coupling it with the predefined Piezoelectric Effect Multiphysics node. The deformation of a piezoelectric device is captured by a moving mesh that reinitializes the numerical representation of the filter geometry for the EM analysis. Then, the cavity-resonant-mode analysis is excited by EM waves, which is analyzed in the given frequency range.
Virtually Realizing Real-World Effects on Your Component Design
COMSOL Multiphysics recently released updates to the RF Module that make it optimal for designing filter-type devices at conventional RF/microwave frequency ranges, as well as higher millimeter-wave (mmWave) and even terahertz (THz) bands. The software enables users to expedite the simulation process through model-order-reduction (MOR) techniques.
Traditional simulation models can be extended to include various physics phenomena that are not easily measured in the laboratory environment, such as heat effects on material properties as well as structural deformation. All of the physics are addressed in the same simulation environment, allowing for a comprehensive look into the design of your device. Whether you design cavity filters for the 5G future or not, it’s imperative to include the real-world phenomena into your simulation model to achieve results that mimic the physical world we live in.
Jiyoun Munn is RF Technical Product Manager at COMSOL.
About the Author
Jiyoun Munn
Technical Product Manager, COMSOL Inc.
Jiyoun Munn is the technical product manager for the RF Module at COMSOL, and a senior member of IEEE. He has two decades of experience in the RF industry, developing over 150 antenna and microwave device prototypes. Munn also holds patents for antenna interrogation systems. He received his MS degree in electrical engineering from the University of Michigan.