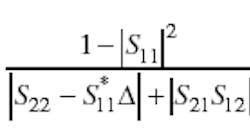Resistive Loading Enhances LNA Stability

where:

Δ= S₁₁S₂₂—S₁₂S₂₁ Parameter µ serves as a figure of merit with increasing values of µ indicating greater stability. As an example, Fig. 1 shows µ computed from manufacturer's scattering parameters (S-parameters) for a model FHR02X HEMT amplifier from Fujitsu Compound Semiconductor. ⁶ It also shows the regions where the amplifier is unconditionally stable and potentially unstable (over most of its frequency range).

To understand the effect of resistive stabilization over a broad range of frequencies, it is necessary to determine the equivalent transmission parameters of a cascaded two-port system that includes the transistor and any stabilizing resistor networks. Figure 2 offers an example, where the first and last two-ports in the cascade each represent one element, either a series or parallel resistor, or a through connection, while the center two-port represents the transistor with transmission parameters computed from its scattering parameters. The stability of an overall network of this type can be found by cascading the transmission parameters, converting from transmission to scattering parameters, and then applying Eq. 1 to determine the value of µ for the overall configuration. Eight different input/output combinations are available for investigation with this technique depending upon whether resistors are connected in series or parallel to one or both of the active device's ports (see table).

Once an amplifier is unconditionally stable, it is possible to determine the maximum transducer power gain, G_Tmax. Parameter G_Tmax is defined as the ratio of the power delivered to the load by the amplifier to the power available from the source under the condition that the amplifier's input and output impedances are conjugately matched, usually through the appropriate design of input and output matching networks. ⁷ The table shows value for G_Tmax for the eight resistor combinations computed at 2 GHz. Increasing the stability factor beyond unity directly reduces the maximum transducer power gain, G_Tmax. For the other six cases equal stability factors lead to equal power gains, as predicted in ref. 8.

Figure 3 shows µ as a function of frequency from 0.10 to 30 GHz, for the nine cases in the table: with no, one, and two stabilization resistors. Networks containing two resistors introduce an additional degree of freedom into the problem. As a consequence, use of a systematic search algorithm is necessary to find input and output resistance combinations that stabilize the transistor. A typical search algorithm for obtaining resistor values consists of a pair of nested loops, with the input resistance value in the outer loop and the output resistance value in the inner loop. Initial resistance values are incremented or decremented, depending on whether the resistor in question is connected in series or in parallel. If the pair of resistors results in an unconditionally stable amplifier, i.e., the stability factor µ, is greater than unity for every frequency examined, the routine reports the resistance values along with the frequency where the minimum value of µ occurs and plots the results as a function of frequency (as in curves 6 to 9 of Fig. 3).

For this work, the search algorithm was designed to identify resistor combinations that stabilize the transistor at all frequencies while providing a stability factor as close to unity at 2 GHz as possible (curves 6 through 9 of Fig. 3). For this particular transistor, it proves possible to adjust the minima of µ for the parallel resistance input/series resistance output (curve 6) and parallel resistance input/parallel resistance output (curve 8) to approximately 10 GHz. The minima of µ for the series resistance input/parallel resistance output (curve 7) and series resistance input/series resistance output (curve 9) combinations was not adjustable.

Figure 3 shows that amplifiers with the parallel resistance input/series resistance output (curve 6) and parallel resistance input/parallel resistance output (curve 8) are stabilized over the entire frequency range without gain penalty at 2 GHz as compared with the four series only/parallel only single resistor combinations that provide stability only over a limited frequency range.

The results of this section demonstrate that, in the particular case of the FHR02X HEMT, all of the eight resistive networks are able to stabilize the amplifier over at least a restricted range of frequencies. In order to apply the technique in a more general way, the stability of a number of other resistively loaded microwave amplifiers were examined by applying the technique presented in this section with all eight resistive networks using manufacturer provided scattering parameters for the different transistors. Most of the results for the eight resistor networks obtained from this investigation are similar to those presented in Fig. 3. For one or two of the resistor networks in the case of some of the transistors, however, no single resistance or combination of resistances was found to result in a value of µ greater than unity at any frequency for the overall resistively loaded amplifier. Thus, the stability improvement due to resistive loading depends strongly on the characteristics of the individual transistors as well as the values of the resistors themselves.

Noise performance is often a critical-factor for microwave amplifiers. While noise is unavoidable, and adding resistance to amplifiers inevitably decreases the output signal-to-noise ratio, different resistive network configurations can have significantly different effects on noise performance. For this reason, it is important to predict the effect of the various resistive stabilization techniques on the overall noise figure of the amplifier in order to facilitate design trade-offs between amplifier stability, gain, and noise performance. A network approach with scattering parameters is feasible because the noise performance of active devices is described in terms of system reflection coefficients. This is illustrated by Fig. 4, which models the resistors as lossy, mismatched two-ports in a cascade network. Amplifier noise is increased by the resistive two-ports as a result of signal attenuation and the impedance mismatch between the cascade-connected ports.

In Fig. 4, considering signals propagating to the right, an input matching network (IMN) transforms the source impedance Z_g into the appropriate source reflection coefficient Γ_S while an output matching network (OMN) transforms the load impedance Z_L into the appropriate load reflection coefficient Γ_L. These matching networks are designed to provide the appropriate impedance transformations necessary to achieve maximum transducer gain, minimum noise figure, or any other amplifier specifications as necessary to meet system requirements.

Page Title

For a two-port described by scattering parameters, usually referenced to 50Ω the respective input and output reflection coefficients, Γ_in and Γ_out, are determined from:

where:

Γ_S= the reflection coefficient looking toward the two-port network's source and

Γ_L= the reflection coefficient looking toward the two-port network's load.

Referring to Fig. 4, sequentially applying Eq. 2 from right to left beginning with Γ_Land scattering parameters 3> allows calculation of the input reflection coefficient Γ_inm for the mth two-port network, where m = 1 to 3. Similarly, sequentially applying Eq. 3 from left to right in Fig. 4, beginning with Γ_Sand the scattering parameters 1> determines the output reflection coefficient Γ_outm for the mth two-port network, where m = 1 to 3. Thus, sequential application of Eqs. 2 and 3 specifies all input and output reflection coefficients for the overall network.

Many authors provide expressions for the noise figure for active and passive components._7,9,10 For active devices the quantities F_min, R_N, and Γ_opt are noise parameters that are characteristic of a particular transistor, while the quantity Z₀ is the system impedance, normally 50Ω. With these definitions the noise figure of a transistor can be expressed as:

where:

F_min = the minimum noise figure of the device,

R_N = the equivalent noise resistance of the device, and

Γ_opt= the value of the optimum source reflection coefficient for the transistor, Γ_S2 (in Fig. 4) that results in a minimum device noise figure.

The available power gain for a two port network is defined as the ratio of the power available from the two-port network to the power available from the source. Mathematically, this is expressed as:

It is important to note that in addition to depending on a two-port network's scattering parameters, the available power gain depends on the reflection coefficients looking out of the input port and into the output port of a two port network.

The noise figure of a lossy two-port network characterized at an operating temperature T is:

where:

T₀ = 290 K and

G_A = the available power gain. Note that at room temperature the noise figure is equal to the power loss factor of the network, L_A or:

so that if the two-port network contains a lossy element, such as a series or parallel connected resistor, the noise figure of the device equals its loss. Thus, it is possible to either increase or reduce the available power gain, Eq. 5, and the resulting noise figure, Eq. 6, depending on the impedance mismatch at the network's ports.

Once the noise figures of the individual two-port networks are available, the overall stabilized amplifier noise figure is found by applying the Friis noise equation: ¹¹

In this situation, subscripts 1, 2, and 3 refer to the two-ports represented by 1>, 2>, and 3>, respectively (Fig. 4). Additionally, in Eq. 8, subscripts 1 and 3 refer to the noise figures and available gain of the lossy two-ports that precede and follow the transistor (Fig. 4) while subscript 2 refers to the noise figure and available gain of the transistor itself. Specifically, F₁ is the noise figure found from Eq. 6 with G_A1 from Eq. 5 for the first resistive network with scattering parameters 1> and reflection coefficients Γ_S1 and Γ_out1. Noise figure F₃ is also found from Eq. 6 with G_A3 from Eq. 5 for the last resistive network with scattering parameters 3> and reflection coefficients Γ_S3 and Γ_out3. Finally, noise figure F₂ for the transistor itself is found from Eq. 4 where G_A2 is the transistor's available gain, Eq. 5, with scattering parameters 2> and reflection coefficients Γ_S2 and Γ_out2.

The final two columns in the table, G_T and F_total, predict the transducer power gain and overall noise figure for the stabilized amplifier when the matching network is designed so that the transistor's input reflection coefficient, Γ_S2, equals the optimum reflection coefficient, Γ_opt. For the example of the FHR02X HEMT, this minimizes the noise contribution, which is 0.33 dB at 2 GHz.

Of special interest in these results is that the series output only (case 4) provides more than 2 dB additional gain and almost 0.1 dB better noise figure performance compared with the parallel output only case (case 5). The parallel input/parallel output configuration (case 8) is unconditionally stable across the entire frequency range and improves the gain by 1.23 dB while suffering only a 0.30 dB degradation of the noise figure compared to the series output only case. These comparisons illustrate the possible choices of a stabilizing network for the amplifier that provides alternative compromises among gain, noise, and stability for a given application.

The results in the proceeding paragraph can be understood from the Friis noise expression (Eq. 8). For example, cases 4, 5, and 8 result in the lowest noise contribution, with cases 4 and 5 lower than case 8. This is because the attenuator follows the transistor, and as Eq. 8 shows, the effect of the noise contribution from the final two-port network is reduced by the relatively large amplifier gains. In the example of case 8, the overall noise figure is slightly worse than for cases 4 and 5 because the attenuation is applied at the amplifier input, and as Eq. 8 shows, the full noise contribution of this two port network appears in the overall noise figure, F_total. This attenuator is relatively ineffective in adding noise, however, because the attenuation and mismatch produced by the parallel connected 5-kΩ resistor is very small compared with the other cases shown. Thus, attenuators at the input and the output do not contribute equally to the degradation of the overall amplifier noise figure, F_total, but the degree of degradation also depends upon the attenuation and mismatch of a specific attenuator, in addition to its location.

Page Title

Four microwave amplifier test circuits were implemented in order to determine the validity of the stability theory and noise predictions for actual microwave amplifiers. The active devices are FHR02X HEMTs, also used as examples in the previous section. Each transistor is attached to a substrate with bond wires, as shown in the example in Fig. 5, with embedded resistors connected in parallel with the input and/or output for three of the amplifiers.

Networks consisting of parallel resistors are convenient from an implementation point of view because inserting a series-connected blocking capacitor eliminates the dc path that otherwise would perturb the transistor's bias. Three amplifiers were constructed with stabilizing resistors designed to be 200Ω but measured in the range of approximately 160Ω to investigate three of the eight different resistive stabilization combinations corresponding to the configurations but not the values of cases 3, 5, and 8; that is, parallel input only, parallel output only, and both parallel input and parallel output, respectively. The design value of 200 W was chosen for the resistors because calculations indicated this value would clearly distinguish between the three cases. A fourth amplifier circuit without resistive stabilization was constructed to allow measurement of the scattering parameters for the transistor itself. Identical bias tees external to the network analyzer provided operating current for each transistor (Fig. 6).

It was not possible for practical reasons to use the same transistor in each test circuit, so the four configurations tested employed distinct physical units. This introduces parametric error into the comparison between the measured and the predicted results because of device-to-device variation in the scattering and noise parameters.

The measured stability parameters shown in Fig. 7 were computed by applying Eq. 1 to measured S-parameters for the three stabilized amplifiers (Fig. 6). The predicted stability parameters shown in Fig. 7 were obtained by applying the method presented in Fig. 2 with measured values of resistance. The difference between predicted and measured values of the stability parameter for the amplifiers stabilized with parallel resistors connected across the input or output amplifier ports is within a few percent to at least 10 GHz.

To verify a portion of the noise predictions of the previous section, noise figure measurements were obtained for two of the FHR02X HEMT microwave amplifiers. This is done by replacing the network analyzer in the test setup (Fig. 6) with an Agilent N8975A noise figure meter from Agilent Technologies (Santa Rosa, CA) driven by an Agilent N4002A noise source (Fig. 8).

Otherwise, test conditions for the amplifiers remain as in Fig. 6.

Figures 9 and 10 show measured and predicted amplifier gain and noise figure for two of the circuits to 26 GHz. Figure 9 shows the measured gain for the FHR02X HEMT with output resistive stabilization obtained from an Agilent E8361A network analyzer, along with the measured gain and noise from an Agilent N8975A noise figure meter. The ripple in the noise figure meter data is attributed to the slight impedance mismatches between the cables and connectors that are necessary to insert the noise figure meter. Otherwise, the correspondence between the two gain measurements is very good. The predicted gain is obtained by following a procedure similar to that shown in Fig. 2 in order to determine the scattering parameters of the overall network. The agreement between the measured and predicted amplifier gain is within a few tenths of a dB to 26 GHz.

Figure 9 also shows the measured noise figure for the same amplifier, as well as a least square quadratic "best fit" of the data to facilitate comparison with theoretical predictions. The predicted noise figure was obtained by applying the procedure discussed in the previous section to the measured scattering parameters for the amplifier obtained here, along with manufacturer provided transistor noise parameters. The disagreement between predicted and measured noise figure is no more than a few tenths of a dB at 10 GHz. Above 10 GHz, a systematic bias appears between the two results that increases with frequency. Additional investigation is necessary in order to determine the cause for this discrepancy.

Figure 10 compares measured and predicted noise figure and gain for the FHR02X HEMT amplifier with input resistive stabilization. The figure shows that locating the resistor at the input port of the amplifier degrades the noise performance by approximately 2 dB compared to the first amplifier. The agreement between measured and predicted results for both figures is similar to what was obtained in the previous case.

In conclusion, a new method has been developed to predict improvements in stability and noise figure due to resistive loading of amplifier input and output ports.^12,13 The approach holds over wide frequency ranges allowing its use for both LNAs and broadband amplifiers, with predicted values within a few tenths of dB for measurements to 10 GHz.

ACKNOWLEDGMENTS
The author would like to acknowledge MIT Lincoln Laboratory for fabricating and characterizing the amplifiers discussed in this article. The author would also like to thank Dr. Mark Gouker of MIT Lincoln Laboratory for providing access to the multichip module-deposited process and to Mr. Rick Drangmeister for his assistance in obtaining the experimental results. The author would also like to express his gratitude to Professor G. Leonard Tyler of Stanford University for generously providing advice and encouragement for this work.

REFERENCES

1. G. Gonzalez, Microwave Transistor Amplifiers, 2nd ed., Prentice Hall, Upper Saddle River, NJ, 1997.
2. David Rosemarin, “A design cure for unstable transistors,” Microwaves & RF, Vol. 23, No. 3, March 1983, pp. 94–95.
3. Les Besser, “Design considerations of a 3.1–3.5 GHz GaAs FET feedback amplifier,” IEEE MTT-S International Microwave Symposium Digest, pp. 230–232, May 1972.
4. George D. Vendelin, “Feedback effects on GaAs MESFET performance,” IEEE MTT-S International Microwave Symposium Digest, pp. 324–326, May 1975.
5. M.L. Edwards and J.H. Sinsky, “A new criterion for linear 2- port stability using a single geometrically derived parameter,” IEEE Transactions on Microwave Theory & Techniques, Vol. 40, No. 12, pp. 2303–2311, December 1992.
6. Fujitsu Compound Semiconductors, Inc., Microwave Products Division, http://www.fujitsu.com.
7. David Pozar, Microwave and RF Design of Wireless Systems, Wiley, New York, 2001.
8. M.L. Edwards and S. Cheng, “Conditionally stable amplifier design using constant m-contours,” IEEE Transactions on Microwave Theory & Techniques, Vol. 44, No. 12, pp. 2634–2640, December 1996.
9. T.H. Lee, The Design of CMOS Radio-Frequency Integrated Circuits, Cambridge University Press, Cambridge, UK, 1998.
10. P.Z. Peebles, Communications System Principles, Addison-Wesley, New York, 1976.
11. H.T. Friis, “Noise figures of radio receivers,” Proceedings of the IRE, Vol. 32, July 1944, pp. 419-422.
12. J.E. Post, “Stability and noise performance of resistively loaded microwave amplifiers,” Microwave and Optical Technology Letters, May 5, 2004, pp. 228–231.
13. J.E. Post, Integration of Microwave and Millimeter Wave Systems in a Precision Multichip-Module Deposited Process, Stanford University, Doctoral Dissertation, 11 May 2005.