Boost In-Situ Reflection Measurement Accuracy with a Portable VNA
Members can download this article in PDF format.
What you’ll learn:
- Understand the network diagram for VNA measurement error terms.
- What are the effects of various residual errors on the outcome of the measurement?
- Learn the only viable solution to the problem of return-loss measurement of a DUT at the end of a lossy feed line.
In the real world, vector network analyzer (VNA) measurements in the field often present obstacles to obtaining accurate readings. In this article, we examine the effect of a long coaxial cable between the VNA and the device under test (DUT), and show the benefit of moving the VNA directly to the DUT.
Error Terms
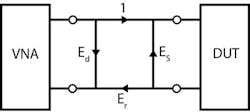
VNA measurement errors are typically modeled with network flow graphs to depict errors due to internal VNA hardware and the effect of external cables and connectors. In the model, the VNA is assumed to be perfect, and all systemic, non-random errors are modeled by an error box between the perfect VNA and the DUT (Fig. 1).
In Figure 1, Ed is the Directivity Error, Es is the Source Match Error, Er is the Reflection Tracking Error, and the forward incident signal is normalized to a value of “1.”
To understand the Directivity Error, one must realize that there’s some leakage in the VNA directional bridge from the incident signal (signal leaving the VNA) to the reflection port of the bridge. Ideally, no signal would be present on the reflection port if there were no reflected signal, but bridges aren’t ideal, and some leakage always exists.
Attenuation of the incident signal and its returning reflection through a lossy cable reduces the desired signal from the reflection port. If the maximum possible reflection at the reflection port of the VNA bridge is reduced and the leakage signal stays the same, then it degrades the effective system directivity.
Source Match error is due to the combination of the error in the source impedance of the VNA compounded by departures from a perfect 50-Ω coaxial environment in the connectors and imperfections of the cable. At the end of the feed cable to the DUT, the effective impedance might be close to, but not precisely, 50 Ω. A DUT with an input impedance of precisely 50 Ω would reflect some of the incident signal in this case. This is the Source Match reflection error.
The Reflection Tracking error accounts for the loss and phase shift from the VNA to the DUT and back again. It generally falls off with frequency as insertion loss through the cable increases.
Residual Error
If calibration is performed on a VNA that has short, low-loss cables with precision connectors, one can expect the residual Directivity (D) to be about 46 dB, residual Source Match (M) to be about 40 dB, and Reflection Tracking (T) to be about ±0.1 dB. Residual values are the effective values after performing calibration with a precision calibration kit.
Expected error on reflection measurements as a function of these residual errors are as follows:
ΔSii = D + T * Sii + M * S2ii + R
where ΔSii is the expected error on the reflection coefficient Sii. D, T, and M are defined above and R accounts for any random uncorrected errors. All terms are expressed in linear format and Sii is used to indicate a one-port reflection measurement on any port.
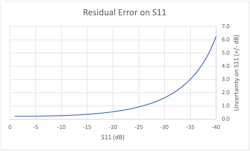
Ignoring random error, for high reflection (Sii near 1) from the DUT, the error is dominated by residual reflection tracking and residual source match. For smaller values of Sii, the error is mostly due to residual directivity. Residual directivity is the hard floor beneath which reflection measurements are ambiguous. In practical terms, once the VNA corrects for the leakage signal as much as possible, any reflection signals on par with the remaining error will have 100% error.
By simple vector addition, reflected signals that are 10 dB higher the residual directivity will have a ±3.3 dB uncertainty and signals 20 dB higher will have ±1 dB uncertainty. To arrive at these two numbers, simply subtract two vectors with one of them 10 and 20 dB smaller than the other. Figure 2 shows a chart of expected uncertainty on S11 for typical residual values of 46, 40, and 0.1 for directivity, source match, and reflection tracking, respectively.
The Long-Cable Problem
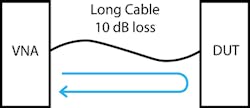
What if one attempts to make a reflection measurement on a long cable? What if there’s 10 dB loss between the VNA and the DUT (Fig. 3)?
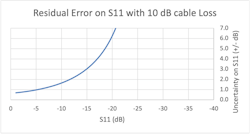
The additional 10 dB will degrade the residual directivity by 20 dB since the incident signal sees 10 dB of loss and the reflection from the DUT sees it as well. If the chart in Figure 2 is updated with directivity degraded from 46 to 26 dB, we get the uncertainty shown in Figure 4.
We see ±3 dB uncertainty for a measurement of 15 dB return loss—not very good at all. There’s no way to remove the loss from the cable so only one simple solution exists: Move the VNA directly to the DUT.
To be clear, in the example just described, it would have been necessary to perform calibration at the end of the long cable. That is, we would have had to detach the cable from the DUT and apply the Open, Short, and Load calibration standards. If we must perform operations at the end of the cable near the DUT, why not just calibrate a VNA and attach it directly?
In Figure 5, a 6-GHz, 1-port, R60 VNA from Copper Mountain Technologies is shown. It isn’t absolutely necessary to calibrate this VNA since it’s calibrated at the factory. Also, the custom precision connector has been designed to add very low uncertainty to the measurement. Because it runs from USB power, it’s a simple matter to bring this VNA directly to the DUT and perform and save the measurement.
For accurate reflection measurements of a DUT at the end of a lossy cable, no other solution is reasonable. Moving the measurement device to the DUT remains the only viable solution and a small, portable device is preferred.
Incidentally, one might think it would help to amplify the output power of the VNA. It does not. Increasing the output power will not change the directivity of the bridge; the leakage signal simply increases with the output power of the VNA.
The same is true if one adds an output amplifier to Port 1 of a 2-port VNA followed by a directional coupler with the reflection port attached to Port 2. This setup works well to isolate the VNA ports from “Hot” spurious signals on the coaxial line. However, reflection uncertainty for small reflections would still be determined by the coupler’s residual directivity after calibration, which would not differ significantly from the residual directivity of the internal bridge for a 1-port measurement made in the usual configuration.
A portable VNA is a powerful addition to the toolkit of any RF professional. This application shows the utility of a small VNA for making otherwise impossible measurements.
About the Author
Brian Walker
Senior RF Engineer SME, Copper Mountain Technologies
Brian Walker is the Senior RF Engineer SME at Copper Mountain Technologies where he helps customers to resolve technical issues and works to develop new solutions for applications of VNAs in test and measurement.
Previously, he was the Manager of RF design at Bird Electronics, where he managed a team of RF Designers and designed new and innovative products. Prior to that he worked for Motorola Component Products Group and was responsible for the design of ceramic comb-line filters for communications devices. Brian graduated from the University of New Mexico, has 40 years of RF Design experience, and has authored three U.S. patents.