The Basics of Radar Technology (Part 1)

What you’ll learn:

• The theory behind radar, including range equations and functional components.
• How range resolution, angular resolution, and velocity equations can help us understand radar system effectiveness.
• What drives gain in various types of radar systems.

With a strong grasp of radar fundamentals comes a foundation for understanding the significance and implications of current trends and innovations in radar technology. Here we’ll cover what radar systems do, what information they can yield, and review their functional components. This includes range equations and variable considerations for searching, tracking, fire control, and imaging radar. 

Radar Functions and Design Parameters

Radar systems detect objects and find their locations in space by transmitting electromagnetic waves in the radio-frequency (RF) and microwave ranges. The system emits short bursts of energy and detects the echo signal returned by objects of interest. That echo signal can provide information on target detection, range, angles, size, speed, and object features.

While ranges differ by application, radar applications span VHF (30 to 300 MHz) to the Ka-band (26.5 to 40 GHz) (Fig. 1).

The radar range equation is used to calculate the maximum range for target detection. Critically, it can be manipulated to understand how different factors are interrelated in the radar system and to implement application-specific design requirements. For example, to find signal-to-noise ratio (SNR), factor in system noise and how the function of interest impacts gain.

The basic form of the radar equation is:

Where:

• 𝑃_𝑡 = power transmitted by the radar
• 𝐺_𝑡 = gain of the transmitting antenna
• 𝐺_𝑟​ = gain of the receiving antenna
• 𝜎 = radar cross-section (RCS) of the target, which represents the target's reflectivity
• 𝜆 = wavelength of the radar signal
• 𝑅 = range to the target
• k = Boltzmann’s constant
• T_s = system temperature
• B_n = noise bandwidth of receiver
• 𝐿 = representation of the system losses due to both the transmitting and receiving processes and the medium through which the radar signal travels

What follows is how we can apply elements of this equation to contextualize different types of radar systems and their requirements by understanding what drives gain under various mission scenarios.

What Drives Gain in Search Radar Systems?

Search radar is designed for object detection. SNR plays a significant role in ensuring the radar system can “hear” the signal reflected by an object regardless of background noise, like picking out a conversation in a crowded room. For search-related applications, the radar system is directed around a space to explore and determine what’s there. SNR must factor in the size of the space and how long the system “looks” in any one direction.

Where:

• P_av = average power
• Α_e = antenna area
• t_s = scan time for Ω
• σ = radar cross section
• Ω = solid angle searched
• R = target range
• k = Boltzmann’s constant
• T_s = system temperature
• L = system loss

To enhance the SNR in search applications, increase average power, antenna size, scan time, and/or target cross-section. SNR is negatively impacted by increasing the solid scan angle of the search area, target range, system temperature, and/or system losses.

Drivers of Gain in Search-and-Track Radar Systems

Search-and-track radar systems incorporate search; however, they continue to follow the target and offer location updates over time. With this form of the radar equation, it’s safe to assume the target was located using search, so scan time and scan angle are less important:

Where:

• P_t = transmitted power
• A = antenna size
• λ = wavelength
• σ = radar cross section
• R = range
• k = Boltzmann’s constant
• T_s = system temperature
• B_n = noise bandwidth of receiver
• L = system losses

To enhance the SNR in tracking applications, increase transmitted power, antenna size, and/or target cross-section. SNR is negatively impacted by increasing target range, wavelength system temperature, receiver noise bandwidth, and/or system losses.

What Drives Gain in Fire Control-and-Imaging Radar Systems?

Because it’s akin to tracking radar in principle and in concept, fire control-and-tracking radar systems are often combined. The main difference is that fire-control radar places additional emphasis on increasing performance via range resolution, angular resolution, and/or velocity resolution:

Increasing Radar Performance Through Range Resolution

The range-resolution variable helps us understand the system’s ability to distinguish between objects. It’s the minimum distance between two objects while still identifying them separately. For a continuous-wave (CW) pulsed radar, for example, range resolution depends on pulse length. The shorter the pulse length, the smaller the distance the system can distinguish. Pulse length is inversely proportional to pulse bandwidth.

Range resolution can be defined as:

Where:

• Δ_r = range resolution
• c = velocity of wave (e.g., the speed of light)
• T = pulse length in seconds
• B = pulse bandwidth in hertz

Increasing Radar Performance Through Angular Resolution

The angular-resolution variable helps us understand the system’s ability to distinguish the distance between two objects at the same range.

Angular resolution can be defined as:

Where:

• S_A = the angular resolution (i.e., the resolvable gap between two objects)
• R = range to target
• ϴ = beamwidth

To reduce antenna beamwidth and resolve smaller distances in a dish array, for example, approximate using:

Where:

ϴ_B = beamwidth

λ = wavelength

D = antenna size

Alternatively, for phased arrays, this can be approximated using:

Where:

• ϴ_B = beamwidth
• λ = wavelength
• ϴ = scan angle of our phased array

Reducing beamwidth and, by extension, improving angular resolution, can be accomplished by reducing wavelength (i.e., increasing frequency), increasing the number of elements in an array, increasing the distance between elements in an array, and by pointing the beam more precisely.

Increasing Radar Performance Through Velocity Resolution

Radar systems can measure velocity via the Doppler effect, which shifts the frequency of the received signal up or down by an amount that’s proportional to the radial velocity of the target. Accurate velocity data requires careful waveform processing and canceling signals reflected from objects that aren’t of interest and might be in the way.

Velocity resolution in a Doppler radar can be defined as:

Where:

• f_d = Doppler frequency
• v_r = radial velocity
• λ = wavelength

One technique for improving a radar’s detection ability is through pulse integration conducted by means of fast Fourier transform (FFT), where integration time can drive velocity resolution via the following:

Where:

• Δ_vr = velocity resolution
• λ = wavelength
• Δ_t = integration time

You can improve velocity resolution by increasing integration time or decreasing the wavelength of the transmitted waves by increasing frequency.

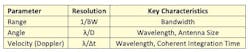
Effectiveness is considered a combination of resolution and accuracy. Changing some of these parameters (Fig. 2) may improve resolution but decrease SNR or vice versa. The role of bandwidth changes depending on the radar application.

Missile-Seeking Radar Systems

Radar systems can direct missiles using semi-active or active radar homing. With semi-active radar homing, a platform-based radar system illuminates the target, and the missile radar receiver interprets the echoes to find it. In active radar homing, the missile contains both the transmitter and receiver.

Whether active or semi-active, missile seekers have SNR needs like those of tracking radar systems and high-resolution requirements like those of fire-control radar systems. That said, it’s important to increase angular resolution without increasing antenna size, which requires increasing the operating frequency from Ku-band to Ka-band.

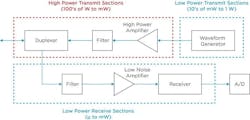
Functional Blocks of Radar Systems

One approach to understanding radar design is to look at the system as a combination of functional blocks that perform key roles (Fig. 3). These functions may be combined or separated across circuits.

The following are the main functional blocks in a radar system:

Waveform generators produce low-power waveforms that can be pulsed or altered in frequency or phase when necessary. Modern waveform generators leverage digital waveform generation (DWG) technology and closely resemble arbitrary waveform generators (AWGs) in function. Here, waveforms are defined by a mathematical model. Using direct digital synthesis (DDS), a digital-to-analog converter (DAC) can generate analog waveforms from digital inputs.

Amplifiers/transmitters take the signal from the waveform generator and increase its power (e.g., hundreds of watts to megawatts).

Duplexers take the high-power signal from the transmitter, ensuring that transmitted and received signals don’t collide.

The signal leaves the antenna, finds the target, and is reflected. The antenna is excited by the incoming reflected radiation, and the received signal passes from the duplexer to the receiver. The receiver amplifies and cleans up the signal before passing it to the digital domain. Depending on the frequencies and sensitivity requirements of the application, different mathematical models can be applied to best serve the system.

The Evolutionary Path of Radar Technology

Here, we’ve laid a foundation for understanding the development path of radar technologies. The advancement of RF and digital electronics plus the desire to improve on key metrics have played significant roles in forging that path. In the next segment of this series, we’ll take a closer look at the ways the evolution of radar has impacted RF components and component selection.