Algorithms to Antenna: Modeling Multistatic Radar Systems
In a previous blog, we reviewed the topic of modeling polarization in radar and wireless systems. Here, we will review an example of how polarization can be used in a multistatic radar. In addition, we describe how detections from multistatic radar systems can be connected to multi-object trackers.
First, a quick introduction. A bistatic radar collects together a bistatic emitter or transmitter (Tx) and a bistatic receiver or sensor (Rx). The typical geometry of a bistatic system is depicted in Figure 1.
1. Depicted is a bistatic radar with an ellipsoid of constant range. The target, transmitter, and sensor all lie in the same plane.
The sensor receives signals along the path, forming the upper sides of the triangle (RT + RR) with bistatic detections referenced to the emitter range. The relative bistatic range is given by:
RBistatic = (RT + RR) − L
where RT is the range from the emitter to the target, RR is the range from the target to the sensor, and L is the range from the emitter to the sensor.
The emitter-to-target-to-sensor range obtained by the bistatic radar is equal to the sum:
(RT + RR) = 2a
This sum defines an ellipsoid of constant range. Figure 1 also illustrates the ellipsoid when the target, transmitter, and sensor all lie in the same plane. This results in a 2D ellipse. The target lies somewhere on the surface of the constant-range ellipsoid with the foci being the emitter and sensor locations, which are separated by the baseline distance L and with a major axis equal to 2a.
Modeling a Bistatic Radar
A bistatic radar system can estimate the range and speed of targets in its field of view. For our first example, we model both the transmit and receive antenna arrays as phased-array antennas of vertical dipoles.
In our example scenario, the receive antenna array, located more than 20 km away from the transmit antenna, is in motion. Two targets are present in the radar coverage. The first one is a point target modeled as a sphere. This means it will preserve the polarization state of the reflected radar signal.
The second target in the scene is modeled such that it flips the polarization state of the incident signal. This means that the horizontal/vertical polarization components of the incident signal become the vertical/horizontal polarization components of the reflected signal.
A single scattering matrix provides a simple polarimetric model for a target. No matter what the incident and reflecting directions are, the power distribution between the horizontal (H) and vertical (V) components is fixed. Even with this simple model, you can see complicated target behavior in the simulation because the H and V directions vary for different incident and reflecting directions. Of course, the orientation of the targets also affects the polarization matching. Figure 2 shows the scenario as simulated over 256 pulses.
2. This is a bistatic radar scenario as simulated over 256 pulses.
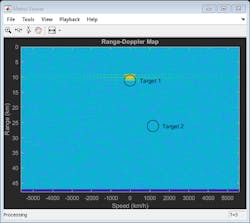
In Figure 3, the top image illustrates a range-Doppler map generated for every 64 pulses received at the receiver array.
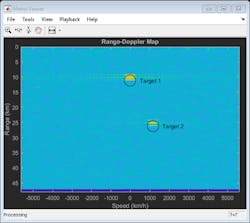
3. The range-Doppler map with the Tx and Rx using the same polarization is shown in the top image, while the results shown in the bottom image were obtained with different polarizations for the Tx (vertical) and Rx (circular).
The range-Doppler map in the top image of Figure 3 shows the return from the first target only. This is because both the transmit and receive array are vertically polarized. The second target converts the vertically polarized wave to a horizontally polarized wave. The received signal from the second target is mostly orthogonal to the receive array’s polarization, resulting in significant polarization loss.
The resulting range and radial speed will not exactly match the range and radial speed of the target relative to the transmitter. This is because in a bistatic configuration, the estimated range is actually the geometric mean of the target range relative to the transmitter and the receiver. Similarly, the estimated radial speed is the sum of the target radial speed relative to the transmitter and the receiver. The circle in the range-Doppler map shows where the targets should appear in the range-Doppler map. Further processing is required to identify the exact location of the target within the circle.
Vertical dipoles are popular choices for transmit antennas in real applications because they are low cost and have omnidirectional patterns. However, if the same antenna is used in the receiver, there’s a risk that the system will miss certain target types. For this reason, a linear polarized antenna may not be the best choice as the receive antenna in this type of configuration. That’s because no matter how the linear polarization is aligned, an orthogonal polarization may be present. In case the reflected signal has a polarization state close to that direction, the polarization loss becomes huge.
One way to solve this issue is to use a circularly polarized antenna at the receive array. A circularly polarized antenna cannot fully match any linear polarization, but the polarization loss between a circular polarized antenna and a linearly polarized signal is 3 dB, regardless of the linear polarization’s direction. Therefore, although it never gives the maximum return, it never misses a target. A frequently used antenna with circular polarization is a crossed dipole antenna.
The bottom image in Figure 3 shows the results when crossed dipole antennas are used to form the receive array. Now the range-Doppler map shows both targets at their correct locations.
Adding a Multi-Object Tracker
Once we generate reliable detections, we can then localize and track multiple targets using bistatic range-only measurements.
Let’s look at a second scenario to generate bistatic detections. We can subsequently use the detections to track the targets. In the second example, we still have a single radar emitter but now there are four receivers. This gives us four bistatic radar sensor pairs to work with.
In simulation, we generate RF emissions, propagate the emissions, and reflect these emissions from the target(s) in the system’s field of view. Of course, the received signals include interference and path losses. We will start with a single target this time because it’s easier to visualize.
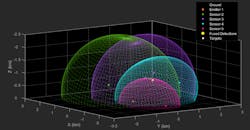
With bistatic measurements, the target lies somewhere on an ellipsoid defined by the emitter and sensor positions, as well as the measured bistatic range. Since the target can lie anywhere on the ellipsoid, a single bistatic measurement does not provide full observability of the target state. Localizing the target (triangulate the target position) and achieving observability of the target’s state requires multiple measurements from different sensors (Fig. 4).
4. Shown are bistatic measurements that indicate the target lies somewhere on an ellipsoid defined by the emitter and sensor positions.
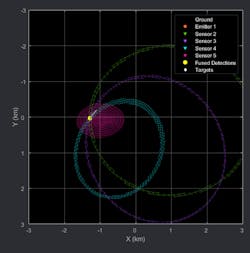
To localize the target, you can look at the spherical intersection (described further in the full example linked at the end of this blog) in Figure 5. The nonlinear nature of the localization problem results in two possible target locations from the intersection of three or more sensor bistatic ranges. A decision about target location from two possible locations can be facilitated by using more than three sensors, which is why we have selected four for this example.
5. Illustrated is the spherical intersection after bistatic detections are combined. The fused detection, denoted by the yellow circle marker, is close to the true position of the target during the scenario.
In our scenario with a single target and no false alarms, multiple measurements can be triangulated to obtain the localized target position. This localized position can be used as an estimate of target position or passed to a tracker to estimate the target state. We calculate the triangulated position of the target, given the bistatic range detections generated by the target.
The fused detection, shown in Figure 5 by the yellow circle marker, lies close to the intersection region generated by the four ellipsoids and is close to the true position of the target during the scenario.
Multitarget Scenario
Our single-target scenario assumes that detections are known to be generated by the same target. Therefore, you can triangulate them to localize the target. However, in a multitarget scenario and in the presence of false alarms and missed detections, this information is usually not available. What results is an unknown data association between detections and the targets.
To solve this problem, you can use a static detection fuser, which estimates the unknown data association between detections and targets and finds the best solution using a multidimensional assignment formulation. With this information, the static detection fuser returns “fused” positional detections of the targets, which can be fed into a centralized tracker.
In the presence of multiple targets and possible false alarms, the ghost intersections may sometimes be more favorable than the actual solution. As these ghost intersections appear randomly in this scenario, they are effectively treated as “false alarms” by the centralized tracker.
To learn more about the topics covered in this blog, see the examples below or email me at [email protected].
- Simulating a Bistatic Polarimetric Radar (example): Learn how to simulate a polarimetric bistatic radar system to estimate the range and speed of targets.
- Tracking Using Bistatic Range Detections (example): Learn how to simulate bistatic range-only detections and localize and track multiple targets.
- Simulating a Polarimetric Radar Return for Weather Observation (example): Simulate a polarimetric Doppler radar return that meets the requirements of weather observations.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
About the Author
Rick Gentile
Product Manager, Phased Array System Toolbox and Signal Processing Toolbox
Rick Gentile is the product manager for Phased Array System Toolbox and Signal Processing Toolbox at MathWorks. Prior to joining MathWorks, Rick was a radar systems engineer at MITRE and MIT Lincoln Laboratory, where he worked on the development of several large radar systems. Rick also was a DSP applications engineer at Analog Devices, where he led embedded processor and system level architecture definitions for high performance signal processing systems used in a wide range of applications.
He received a BS in electrical and computer engineering from the University of Massachusetts, Amherst, and an MS in electrical and computer engineering from Northeastern University, where his focus areas of study included microwave engineering, communications, and signal processing.
Honglei Chen
Principal Engineer
Honglei Chen is a principal engineer at MathWorks where he leads the development of phased-array system simulation. He received his Bachelor of Science from Beijing Institute of Technology and his MS and PhD, both in electrical engineering, from the University of Massachusetts Dartmouth.