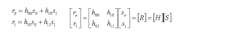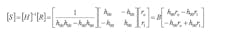Taking a Closer Look at MIMO Radio Systems
Download this article in PDF format.
This article introduces the rationale and techniques associated with multiple-input, multiple-output (MIMO) based communication systems. The communication impairments due to multipath channels are discussed to provide the base motivation for the application of the MIMO technique. In particular, it explores the use of orthogonal frequency-division multiplexing (OFDM) and spatial multiplexing for equalizing broadband wireless channels with non-selective fading.
Fading Channels
The presence of multiple reflections and multiple communication paths between two radio terminals causes signal fading impairments to a wireless-communication link. Both selective and non-selective fading exist. Non-selective fading happens when the frequency components over the signal bandwidth are dynamically attenuated by the same amount and do not create any signal distortion—only temporal signal loss. Selective fading is the case when smaller frequency segments of the signal’s spectrum are attenuated relative to the other remaining frequency segments. When this occurs, the signal spectrum is distorted, which in turn creates a communication impairment that’s independent of signal level.
For narrowband signals with non-selective fading, the communication impairment can be countered by providing more signal-level margin in the communication link or using selection-diversity techniques to select the best antenna input based on the relative signal strength. However, in the case of non-selective fading, the signal must be equalized to restore the signal fidelity and expected communication performance.
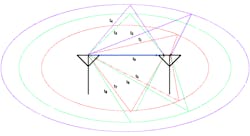
This fading is produced by the arrival of multiple replicas of the transmitted signal at the receiving antenna. The signal replicas are produced by multiple random reflections within the communication medium, such as an indoor communication channel. Figure 1 shows the multipath concept for reference. It’s based on the notion of an ellipsoidal fading model.1
1. This is a multipath channel model illustration.
Consider the case in which a simple two-ray fading model is constructed and the signal attenuation versus communication range is able to be generated. One will find the presence of crests and nulls due to the constructive and destructive interference caused by the arrival of the signals at different delay times, leading to difference phase angles. In some cases, the phase angle can be at or near 180 degrees and can cause partial signal cancellation.
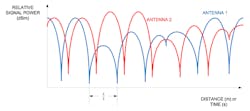
Conversely, signals that are in-phase may cause partial signal enhancement. Figure 2 shows the attenuation profile for a two-ray fading model. Note the periodic signal nulls as the communication range changes. The period of the null spacing is one-half wavelength.
2. Shown are multipath effects on attenuation versus communication range for a two-ray model.
Antenna Diversity
As mentioned previously, the effects of this localized and sudden attenuation can be compensated by receiving the signal at two different receiver-antenna placement locations and selecting the best antenna based on the signal strength or some other receiver performance measure. Figure 3 illustrates this situation by showing the signal strength at two different antenna placements over communication range and/or time. The point of the illustration is that the signal strengths associated with the antennas generally are not correlated in time and/or space. When one signal is in a null, the other can be found near a maximum and selected for communication.
3. Relative signal strength is depicted for two receive antenna locations within a multipath channel.
Selecting one antenna over the other based on signal quality, or selection diversity, is a technique that works well for non-selective fading. That’s because antenna selection is essentially a signal-strength restoration technique. The effects of antenna diversity for a Rayleigh fading channel result in a 17.5-dB gain in performance. Note that the same performance can be achieved by introducing additional signal-level margin of 27.5 dB without the additional antenna and selection scheme.
Selective Fading
However, for broader band signals more commonly used in modern wireless systems like wireless LAN, selection diversity and other signal-strength restoration techniques are not enough to equalize the impairments imposed by the multipath channel due to selective fading.
Selective fading occurs when the signal bandwidth exceeds the coherence bandwidth of the channel.2 The coherence bandwidth of the channel is approximately the reciprocal of the delay spread of the channel.2 The delay spread is the rms average of the delay times of the channel’s complex impulse response. The channel’s impulse response is the received complex envelope at a particular point in space, assuming that a carrier signal is modulated by a Dirac impulse. The arrival of the various signal components can be modeled by a finite-impulse-response (FIR) filter.
Ideally, the channel transfer function only adds a flat fading process (constant attenuation versus frequency) and a single fixed time delay (linear phase). However, some cases result in the creation of a transfer function for the signal that provides asymmetric and frequency-dependent fading of amplitude, as well as a nonlinear phase response, assuming that significant sidebands of the signal are distributed across the entire transfer function.
If the sidebands of a complex modulated signal were distributed across the transfer function, there would be significant signal distortion and modulation conversion (AM to PM and PM to AM). This is again the effect of a multipath channel with a coherence bandwidth that’s less than the signal bandwidth.
To compensate for these effects, the transfer function encountered via the communication channel must be equalized at the receiver. Ideally, if the inverse of the transfer function could be applied to the signal prior to detection to flatten the amplitude response and linearize the phase, the signal impairments would be eliminated.
Several different types of transversal equalizers operate on the time-domain representation of the baseband signal to achieve the equalization. However, many rely on training sequences and training periods (receipt of non-information bearing training information that creates communication overhead).
OFDM and Channel Equalization
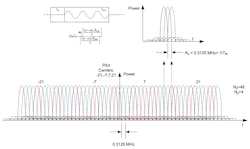
The introduction of OFDM signaling provided a means of spectrally efficient communications and a means for channel equalization in the frequency domain. Figure 4 shows a diagram of an OFDM spectrum, revealing 48 data subcarriers and four pilot subcarriers. The pilot subcarriers are not information bearing, but rather are used to help maintain the carrier and timing tracking in low-signal-to-noise ratios since they are always BPSK modulated.
4. Three isolated subcarriers are present in this construct of an entire OFDM spectrum. Revealed is subcarrier spectrum that arises from amplitude masking by FFT interval and guard interval.
OFDM essentially offers a way to sample the magnitude and phase of the channel at any or all of the subcarrier frequencies, since the carrier phase tracked at the receiver and all subcarrier phases are coherent to the main carrier. However, in practice, performing continuous subcarrier phase tracking on each of the subcarriers is not executed. Rather, short and long training symbols with known patterns are transmitted with each packet. Therefore, the receiver can determine the channel transfer function, invert it, and then apply the inverse to the received spectrum to equalize the channel on a packet-by-packet basis.
5. Depicted is the channel transfer function effect on OFDM spectrum. Each subcarrier has its magnitude and phase altered, but can be sensed and used to generate an equalization filter transfer function.
Figure 5 illustrates how the channel transfer function due to selective fading weights the received spectrum. At the receiver, the magnitude and phase of each subcarrier provide an estimate of the channel transfer function, Hc(ω). An equalization transfer function, He(ω), can be applied to the channel-weighted spectrum to re-normalize the spectrum in order to reduce or eliminate the effects of the channel.
Multiple-Input, Multiple-Output Systems
The previous sections discussed multipath channels, non-selective fading, selective fading, and OFDM signaling. Furthermore, it was shown that antenna selection diversity is a technique for improving the performance in a non-selective fading channel and that OFDM provides for channel equalization against frequency-selective fading. This section digs into the MIMO technique, essentially bringing two elements together: OFDM and antenna diversity.
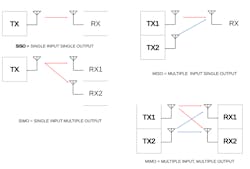
In general, different permutations of redundant transmitters and receivers improve the robustness of a communication link as well as its information carrying capacity. Figure 6 shows the different general redundancy configurations: single-input, single-output (SISO), single-input, multiple-output (SIMO), multiple-input, single-output (MISO), and MIMO.
6. Shown are several communication system configurations.
SISO systems do not provide any type of robustness or capacity improvement. They represent a basic wireless communication link. SIMO systems are configurations that provide receive-side diversity and provide additional robustness, but no capacity improvement. Examples of SIMO systems are receivers with selection-diversity schemes or linear-maximal-ratio-combining (LMRC) schemes.2
MISO offers transmitter diversity in that it couples to the channel at different points in space. Thus, the links will not have the same fading characteristics to the receive antenna and the spatial sum of the signals will be dominated by the stronger of the two signals. Or the transmitter signal design can be such that the combining at the single receiver can be made in an optimal fashion, as is done in space-time coding techniques.2 MIMO systems de-multiplex the source data stream into multiple independent channel streams, allowing for both redundancy and channel-capacity improvement.3
The MIMO technique is also referred to as spatial division multiplexing. A single source data stream is multiplexed between two spatial streams. As shown in Figure 6, direct links and cross links exist between the two transmitters and two receivers. As a result, four different communication channels now connect the two terminals, and the characterization of the channel has a higher complexity. However, the signaling technique when combined with the properties of OFDM modulation can lead to an efficient channel estimation and equalization scheme.
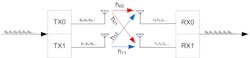
Figure 7 shows the spatial-multiplexing scheme in which even signals are transmitted on TX0 and odd symbols are transmitted on TX1. The two receivers, RX0 and RX1, receive both transmitted streams through four possible channel transfer functions: h00, h01, h10, and h11. These form a channel matrix, [H].
7. In this case, 2-×-2 MIMO is a spatial multiplexer.
To equalize and extract the source symbol stream, an estimate of the channel matrix, [H], must be made. This can be accomplished by transmitting both streams using a coordinated system of pilot subcarriers and null subcarriers (Fig. 8).
8. Here, 2-×-2 coordinated pilot subcarriers and null subcarriers are at each transmitter.
Figure 9 represents the received spectrum, showing that relative levels of each subcarrier indicate relative levels between the direct and cross channel terms in the channel matrix [H].
9. The received spectrum at RX0 shows the relative levels of h00 and h10 from the pilot subcarrier levels.
The received symbols at each of the receive inputs can be computed as follows:
For the case of pilot subcarriers relative to the null subcarriers:
Since the magnitude and phase of pilot subcarriers is known, the s-terms can be factored out and the elements of the channel matrix are determined. Given the channel matrix, the received signals can be equalized and restored according to:
Note that the originally transmitted signals can be restored perfectly if there’s a perfect estimation of the channel matrix. One case that does not work due to a singularity in the matrix inversion is when all of the channel elements are equal or correlated:
The denominator of the leading term associated with matrix inversion determinant will equal zero, causing the singularity. Therefore, MIMO systems operate the best when the individual channel elements are not correlated.
The spatial-multiplexing technique associated with MIMO is another method that minimizes the effects of a multipath communication channel through its redundancy and channel-equalization properties.
Brian Petted is Technology Leader at Laird Connectivity.
References
- Diagram after: “MIMO Channel Modeling and Emulation Test Challenges,” K.Bertlin, Agilent Technologies, 2008.
- C. Oestges and B. Clerckx, “MIMO Wireless Communications,” Academic Press, 2007.
- B. Holter, “On the Capacity of the MIMO Channel- A Tutorial Introduction,” Norwegian University of Science and Technology, Department of Telecommunications, O.S.Bragstads plass 2B, N-7491 Trondheim, Norway.