Overcome Message Collisions in Satellite Automatic ID Systems
Download this article in PDF format.
Ed.: We'd also like to recognize co-author V. Sambasiva Rao, Director, Centre for Research in Space Science and Technology, PES University, Bengaluru, India, and Professor, ECE Department of PES University, Bengaluru (and keeper of S-band satellite ground station at PES University for interested students).
Ocean-going ships rely on various types of signals from space satellites for guidance. At times, maritime vessels can struggle to resolve overlapped Gaussian minimum shift keying (GMSK) signals as part of the Space-Based Automatic Identification System (SB-AIS).
Fortunately, a practical technique based on the use of blind source separation (BSS) can resolve overlapped SB-AIS signals. It implements an independent component analysis (ICA) method to extract component values from the mixture of AIS signals received by a satellite receiver from different ship sources. Tracking component signals can be accomplished by estimating mixing components and accumulating a set of mixed GMSK signals. In fact, the approach is robust enough to receive transmitted symbol sequences despite different Doppler shifts in the received signals.
Use of the satellite-based AIS is required by the International Maritime Organization (IMO) for guidance of ships of class 300 tons and larger when on the high seas. The AIS is designed to avoid collisions between ships and used for terrestrial applications.1 It employs self-organized time-division multiple access (SOTDMA) as an access scheme. AIS transceivers in each ship continually transmit each vessel’s key data, such as its identification (ID) code, position, course, and speed toward other nearby ships.2,3
It also transmits ship details to the AIS stations along coast lines using the VHF maritime frequency band. AIS transponders transmit and receive data at 9.6 kb/s4 using GMSK frequency modulation (FM) over the two frequency channels of 161.975 MHz and 162.025 MHz of 25-kHz (Class A) bandwidth. Each SOTDMA frame has one-minute duration that’s divided into 2250 time slots. The transmission power (for Class A transponders) is 12.5 W.4
Message…Received?
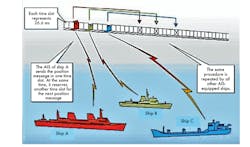
Conventional VHF communication between a ship and the shore or one ship to another ship is constrained by the horizon, typically to 40 nautical miles.5 The limitation of terrestrial coverage is overcome by the SB-AIS.6 In the SB-AIS system, low-earth-orbit (LEO) satellites receive AIS signals from various ships located over a wide area on the Earth. The allocation of AIS message slots is self-coordinated within a limited area referred to as a cell. During the visibility of the satellite to a ship, several such organized cells are covered simultaneously. AIS messages sent in the same time space from various self-coordinated regions will be received by a satellite at the same time, resulting in the collision of AIS messages.
AIS messages sent in adjacent time slots from different organized areas may also overlap partly because of the different path distances.7 This causes serious signal interference at the spacecraft. Hence, there’s a total reduction in the probability of detection of the AIS messages when the satellite passes over areas with high traffic density.
The main challenge is to overcome the interference between messages received from various organized areas and to extract individual ship data. Fortunately, a technique with a signal-separation algorithm can be used to separate the overlapped GMSK signals. It successfully mitigates the slot collision problem associated with the received mixed AIS signals under maximum Doppler shifts/time delay due to different path-loss conditions.
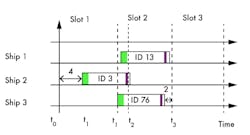
1. This plot presents examples of timing collisions among the communications to satellite for three different ships.
Signals transmitted from the AIS systems onboard ships in a satellite antenna’s coverage zone are received by the satellite receiver onboard a LEO satellite. Signals transmitted by ships in different areas within the same time slot result in the collision of AIS messages.8 The signals transmitted within each slot are received by the satellite with different amplitudes, time delays, and different Doppler frequency shifts due to the spatial separation of the ships. Fig. 1 depicts the slot collision of AIS messages.
As per statistical observations, the probability of receiving more than three ship signals in each slot at the satellite simultaneously is quite low.2 For this reason, three signals are simulated to test the effectiveness of the proposed signal separation technique. At each time instant, the received signal is a mixture of AIS messages with a certain amplitude ratio. This ratio depends on received power level and channel characteristics. Equation 1 gives the received mixed signal X at each instant of time as a mixture of three ship signals (S1, S2, and S3) with different amplitude ratio. The amplitude ratios associated with S1, S2, and S3 are taken as A1, A2, and A3, respectively:
A1S1 + A2S2 + A3S3 (1)
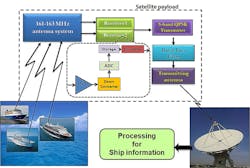
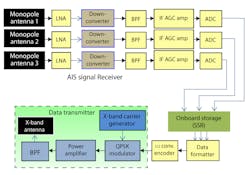
Figure 2 presents a schematic diagram of the proposed advanced SB-AIS architecture. Three ships are assumed to be transmitting in a time slot in the satellite visible zone. The transmitted signals are received by three VHF monopole antennas mounted onboard a LEO satellite. The three VHF antennas are placed with spatial separations equal to fractional wavelengths of the transmitted frequencies. The mixtures of the three signals are received by three separate high-sensitivity VHF receivers onboard the LEO satellite, frequency-downconverted, digitized, and multiplexed into a single data stream and stored using a solid-state recorder (SSR).
2. The block diagram represents a satellite-based AIS.
During the satellite visibility period, the stored digital data is transmitted to ground by quadrature-phase-shift-keying (QPSK) modulation of an S- or X-band carrier. At the ground station, the received compound signal is demodulated, demultiplexed, and processed using the proposed signal separation algorithm to extract individual ship data.
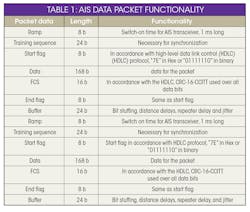
3. This is the structure of an AIS data packet.
The AIS transmitter part of the AIS transceiver placed onboard the ship includes AIS message and SOTDMA formatter and Gaussian-minimum-shift-keying (GMSK) modulation. Its 256-bit data form a data packet for transmission in each 26.6-ms slot (Fig. 3). Table 1 describes the bit size, timing, and functionality of each frame of the data packet. The carrier is GMSK-modulated with the formatted AIS data stream.
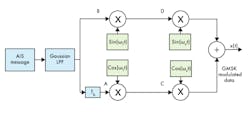
GMSK is a modulation technique that prefilters the incoming signal using a Gaussian pulse-shaping filter and performs MSK modulation.9 The bandwidth of the filter is chosen based on BT value, which is the product of the premodulation Gaussian filter bandwidth (B) and bit period (T).10 Fig. 4 presents a block schematic diagram of the GMSK modulator.
4. This block diagram represents a GMSK modulator unit.
The AIS channel access scheme is based on SOTDMA, in which total transmission time for each AIS frame is 1 min and contains 2250 slots. Each AIS slot contains 256 bits of formatted data that’s transmitted within 26.6 ms. AIS-enabled ships continuously synchronize themselves with GPS time in order to avoid slot collisions. Slot selection of each AIS station is randomized within a defined interval. The SOTDMA channel access scheme is shown in Fig. 5. When a station changes its slot location, new location and timeout for the same are announced beforehand. As a result, new slot location, including modified ship slot and new slot for ships in radio visibility, will be received by all vessels in a coverage area.
5. Shown is an SOTDMA channel scheme for three ships communicating with a satellite.
Lots of Slots
According to IMO, a minimum of 2000 time slots per minute is the reporting capacity of AIS-equipped ships. When the slots are shared in the SOTDMA broadcast mode, it overloads the system by 400-500%. In the case of communication between the ships within a range of 8 to 10 nautical miles, throughput is 100%. When the system gets overloaded, the preference is given to nearer rather than farther targets.
6. The components on board an AIS include frequency downconverters, filters, and amplifiers of several kinds.
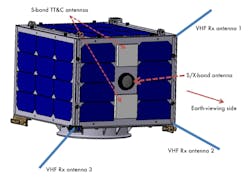
The proposed onboard receiver architecture contains three VHF monopole antennas, three receivers—each consisting of a low-noise amplifier (LNA), frequency downconverter, intermediate-frequency (IF) automatic-gain-control (AGC) amplifier—and an analog-to-digital converter (ADC). The three outputs are multiplexed and stored onboard the SSR. An S/X-band transmitting unit facilitates data transmission during the ground-station visibility period. Fig. 6 gives an overview of an onboard AIS receiver and transmitter architecture. As Fig. 7 shows, three monopole antennas designed for VHF are mounted on three corners of the Earth-visible panel of the satellite. Each antenna output is connected to a dedicated receiver.
7. Antennas of different frequencies are configured on an AIS satellite.
The signals received by the three dedicated receivers are passed through individual LNAs, downconverters, and bandpass filters (BPFs) to reach a baseband frequency of 480 kHz. The downconverted signals are digitized by an ADC, which samples the input analog signal at a rate of 10 times the baseband signal frequency (4800 kHz). The digitized data streams are multiplexed and then stored within an SSR.
During the period during which the satellite is visible to Earth, the stored or real-time data is QPSK-modulated on an S- or X-band carrier, depending on spectrum availability. The modulated carrier is transmitted by an S- or X-band antenna. An antenna designed for transmitting an S/X-band QPSK modulated carrier is mounted on the Earth-visible panel of the satellite. The antenna is designed with a beamwidth of about 130 deg.
The three mixed signals (X1, X2, and X3) are received from the three monopole antennas. The ratio of each ship transmitted signal S1, S2, and S3 in a mixture Xi (i = 1, 2, 3) is based on the channel characteristics and received power level. The ratio vectors of each mixed signal differ from the others based on the antenna placements from each other. Mathematically, the three mixed signals X1, X2, and X3 received by the three monopole antennas are expressed by Eqs. 2 through 4:
X1 = A11S1 + A12S2 +A13S3 (2)
X2 = A21S1 + A22S2 + A23S3 (3)
X3 = A31S1 + A32S2 + A33S3 (4)
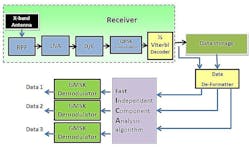
For this model, three antennas separated by fractional wavelengths of the frequencies of interest are mounted on the satellite. Three receivers will receive the mixed signals with their relative phase differences. Fig. 8 shows the configuration of the ground station. The ground station receives the signals transmitted by satellite, demodulates them, demultiplexes them, and applies the signal separation algorithm to separate the signals, which are further GMSK-demodulated to discover individual ship data.
8. This is a block diagram of the ground station for a self-correcting AIS setup.
The received S/X-band signals pass through a receiver with an LNA and then downconverted to a 480-kHz IF. The IF signal is demodulated, Viterbi decoded, and demultiplexed to get the three signals X1, X2, and X3. The three signals are separated using the Fast ICA Technique detailed subsequently in this article. The recovered ship-transmitted signals S1, S2, and S3 are in modulated form with a carrier frequency of 480 kHz. The data is recovered using independent GMSK demodulators.
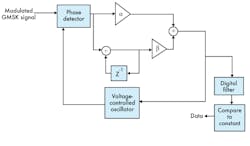
Demodulation of the GMSK signals is performed using the digital phase-locked loop (DPLL) shown in Fig. 9.12 It consists of a phase detector, proportional-integral loop filter, and voltage-controlled oscillator (VCO).
9. GMSK signals are demodulated by means of this setup.
The two inputs to the phase detector are the input and the output of the VCO. The phase detector is a digital multiplier that generates an error signal proportional to the phase error between the input signal and the output of the VCO. The type 1 loop filter, a π-controller, is part of the PLL’s means of tracking phase and frequency. The π-controller consists of two arms: a proportional arm and an integral arm as indicated by the transfer function of a type 1 loop filter in Eq. 5:12
Fs = Kp + KI/s (5)
where the proportional arm gain (Kp) produces the signal for small values of phase error. Parameter β controls the proportional gain.
The integral arm gain (KI) produces the response proportional to changes in the frequency and maintains the DC bias. The α parameter controls the proportional gain. The output frequency of the VCO is controlled by the input error voltage. The VCO output frequency increases from free-running oscillator frequency (under zero input voltage) continuously until the output frequency of the VCO is equal to the input signal frequency.
Fast “Independent Component Analysis (ICA)”is a powerful BSS technique13,14 to separate and recover the source signals S1, S2, and S3 from the mixed antennas’ signals X1, X2, and X3. The modulated signal has a property of non-Gaussian distribution and is statistically independent. According to central limit theorem, due to the mixing of signal vector S by mixing matrix A, the mixed signal possesses a Gaussian distribution and the signal components are correlated. Fast ICA15 is a signal-processing technique that processes the ship signal data in the mixed signal by de-correlating the mixed data and maximizing the non-Gaussianity.
The relationships between mixed signals X1, X2, and X3 and modulated ship signals S1, S2, and S3 in terms of matrices can be expressed as in Eq. 6:16
X=A*S (6)
where:
and
Vector X is preprocessed by centering and sphering (for de-correlation).17
The Fast ICA process locates the mixing matrix A and performs A – 1 processing to recover the ship-signal vector Y, expressed mathematically by Eq. 7:
Y = W*X (7)
where:
W = (w1, w2, w3)T = A-1
is the unmixing matrix. The objective function is based on maximizing the non-Gaussianity in the mixed signals to recover the ship data as given by Eq. 8:15
JG(Yi) = [E{G(Yi)} – E{G(γ)}]2 (8)
where G is the cubic function given by G (u) = u3; Yi is the ith sample of the mixed-signal vector; and γ is the random Gaussian variable of zero mean and unit variance. To obtain the recovered signal vector Y, the objective function JG(Yi) must be maximized.
Based on the signal projection pursuit direction, to find one independent modulated ship signal under the constraint:
║wi║2 = 1 for i = 1, 2, 3
Eq. 8 is rewritten as Eq. 9:15
JG(wi) = [E{G(wiTX)} – E{G(γ)}]2 (9)
According to the Kuhn-Tucker condition, the local maxima of the function JG(wi) under the norm constraint are at places where Eq. 10 is satisfied:
E{Xg(wiTX)} – βwi = 0 (10)
where g = G´; β = E{w0TXg(w0TX)}; and w0 is the value of w at optimum.
Considering Eq. 10 as a function of (wi) given in Eq. 11:15
f(wi) = E{Xg(wiTX)} – βwi (11)
After solving Eqs. 10 and 11 via the Newton Raphson method, an iterative equation given by Eq. 12 yields:
wi(n + 1) = wi(n) – f(wi)f´(wi) (12)
The Jacobian matrix f´(wi) can be obtained as in Eq. 13:
f´(wi) = E{XXTg´(wiTX)} – βI (13)
As a result, the weighting update is given by Eq. 14:15
wi(n + 1) = wi(n) – [E{Xg(wiTX)} – βwi]/[E{XXTg´(wiTX)} – βI] (14)
For a fixed convergence of Newton’s method, converging factor µ is added to the equation, resulting in Eq. 15:15
wi(n + 1) = wi(n) – μ[E{Xg(wiTX)} – βwi]/[E{XXTg´(wiTX)} – βI] (15)
where μ is a step-size parameter that changes dynamically with the iteration count. The value of μ ranges from 0.001 to 1.15
Considering flexible convergence and solving Eq. 15 by premultiplying it with [β – E{g´(wiTX)] yields Eq. 16:
wi(n + 1) = E{Xg(wiTX)} – E{g´(wiTX)}wi (16)
To estimate all of the independent ship data signals, Eq. 1615 is iterated for all values of i = 1, 2, 3.
Once all independent weighting vectors wi are estimated, to prevent different weights converging to the same estimated ship signal, decorrelation of the weighting vector w1, w2, and w3 after every iteration is carried out. A symmetric decorrelation technique is carried out for this purpose. A two-step algorithm for the symmetric method is:
Step 1: Normalization of the updated weight as in Eq. 17:
Wnorm (n + 1) = W(n + 1)/[║W(n + 1)WT(n + 1)║]0.5 (17)
Step 2: Repeat Eq. 18 until reaching convergence:
W+ = (3/2)Wnorm – (1/2)WnormWnormTWnorm (18)
The updated weighting vector (W+) is the unmixing matrix obtained through the Fast ICA procedure. The matrix is used in Eq. 7 to obtain the estimated signal vector Y transmitted by a ship.
Implementing the Algorithm
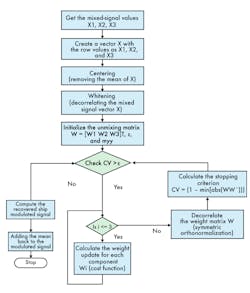
The flowchart in Fig. 10 explains the steps involved in implementing the Fast ICA algorithm as MATLAB m-code.
10. This flowchart represents the functional operation of the Fast ICA system.
Step1: Obtain the mixed signals X1, X2, and X3 from the receiver unit.
Step 2: Construct the matrix X as [X1 X2 X3 ]T and initialize the demixing matrix W as:
Step 3: Centering of vector X as in Eq. 19:
X = X – E{X} (19)
Step 4: The whitening step, where the centered vector X is converted by linear transformation to a new vector with elements uncorrelated to each other. The transformed vector Z is expressed by Eq. 20:
Z = D-0.5ETX (20)
Step 5: Compute the weighting-update step for all the components of weight vector W1, W2, and W3 by iterating Eq. 16 for i = 1 to 3.
Step 6: Perform symmetric orthonormalization to decorrelate the entire weighting vector W1X, W2X, and W3X.
Step 7: Check for the stopping criterion, {1 – min[abs(WWT)]} > ε. If satisfied, proceed to step 5.
Step 8: Compute the recovered modulated signal from vector W by using Eq. 13.
Step 9: Add the mean back to the recovered signal as in Eq. 21:
S + A-1m (21)
where m is the mean obtained in the centering step and A-1 is the demixing matrix.
Step 10: The recovered modulated signal has the same signal information as the original ship transmitted signal and can be demodulated through GMSK demodulator to recover the data.
Checking Results
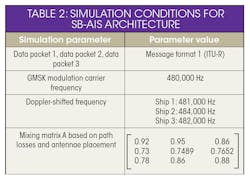
The SB-AIS system architecture was simulated in a MATLAB- SIMULINK computer software environment. Even with a minimum difference of 0.0001 for the ratios of the three signals, all three ship data packets were recovered by using the algorithm. The simulation conditions, assuming one typical scenario as an example, are specified in Table 2. The mixing matrix can be a random matrix and a maximum Doppler frequency of ±4 kHz, so each ship carrier frequency can vary by as much as 480 ± 4 kHz.
In the simulation, source signals are three modulated GMSK signals with three different data sequences in Message 1 format as recommended by ITU-R. The modulated signals of the ships are multiplied by mixing matrix A (Table 2, again) to obtain the mixed signal. The sample length of mixed signal X and recovered ship signals Y are both 12401 in the simulation.
The novel approach successfully resolves AIS message collisions by means of signal processing. The technique of maximizing the cost function through iterative processing of time-series data to retrieve the AIS messages is exploited as a reliable solution.
The proposed innovative architecture incorporated with the blind source separation technique in a MATLAB/Simulink environment exhibits the capability to track a wide range of carrier frequency shift and has an excellent resistance to the path loss variations. The advanced receiver architecture can be implemented as a suitable scheme for an SB-AIS with high detection probability of ships in the coverage area.
Acknowledgments
The authors would like to thank Professor Brij Mohan, Member Secretary, Naval Research Board, New Delhi, and Commander Dr. Vijay Singh, Naval Research Board, New Delhi and Naval Research Board (NRB) for the encouragement to take up the work. The authors would also like to offer thanks for the support given by Dr. K. N. B. Murthy, Vice-Chancellor, PES University, Bengaluru, India. Furthermore, the technical support provided by Dr. J. Manikandan, Professor, Department of ECE, PES University, Bengaluru, India, is highly appreciated.
References
1. Paolo Burzigotti, Alberto Ginesi, and Giulio Colavolpe, “Advanced receiver design for satellite-based automatic identification system signal detection,” International Journal of Satellite Communications and Networking, Vol. 30, 2012, pp. 52-63.
2. Ole Fredrik Haakonsen Dahl, “Space Based AIS Receiver for Maritime Traffic Monitoring Using Interference Cancellation,” NTNU Innovation and Creativity, June 2006.
3. Changchuan Lin, “AIS System and the Applications at the Harbour Traffic Management,” 4th International Conference on Wireless Communications Networking and Mobile Computing, 2008.
4. ITU-R, “Technical characteristics for an automatic identification system using TDMA in the VHF maritime mobile band,” Recommendations ITU-R M.1371-4 (04/2010).
5. Qing Hu, Yi Jiang, Jingo Zhang, Xiaowen Sun, and Shufang Zhang, “Development of Automatic Identification System Autonomous Positioning System,” Sensors, Vol. 15, 2015, pp. 28574-28591.
6. G. K. Hoye, T. Eriksen, B. J. Meland, and B. T. Narheim, “Space-Based AIS for Global Maritime Traffic Monitoring,” Acta Astranautica, Vol. 62, Nos. 2-3, 2008, pp. 240-245.
7. Torkild Eriksen, Gudrun Hoye, Bjorn Narheim, and Bente Jenslokken Meland, “Maritime traffic monitoring using a space-basedAIS receiver,” Elsevier Science Direct, Acta Astronautica, Vol. 58, No. 10, May 2006, pp. 537–549.
8. Andis Dembovskis, “AIS Message extraction from Overlapped AIS signals for SAT-AISapplications,” doctoral dissertation, Universität of Bremen, Bremen, Germany, March 2015.
9. Shou-zhong Zhu, Xiao-ling Wang, Wen-li Jiang, and Xi-xiang Zhang, “Combined iterative cross-correlation demodulation scheme for mixing space borne automatic identification system signals,” Journal of Central South University, 2013.
10. Shou-zhong Zhu, Zheng Liu, and Wen-li Jiang, “Counteraction of Constant Modulus Demodulation Scheme for Mixing Space Borne AIS Signals,” Applied Mechanisms and Materials, 2013.
11. Behzad Razavi, RF Microelectronics, 2nd ed., University of California, Prentice Hall PTR, 2012.
12. Justin Gaither, “Digital Phase Locked Loop (DPLL) Reference Design,” Xilinx XAPP854 (V1,0), October 10, 2006.
13. Zhu Shou Zing, Liu Zheng, Jiang Wen Li, and Guo Kun, “The Key Technology of Blind Source Separation of Satellite-Based AIS,” International Workshop on Informatics and Electronics Engineering (IWIEE), 2012.
14. Adel Belouchrani, Member, IEEE, Karim Abed-Meraim, Jean-Francois Cardoso, Member, IEEE, and Eric Moulines, Member, IEEE, “A Blind Source Separation Technique Using Second-Order Statistics,” IEEE Transactions on Signal Processing, Vol. 45, No. 2, February 1997.
15. Aapo Hyvarinen, “Fast and Robust Fixed-Point Algorithms for Independent component Analysis,” Helsinki University of Technology, Laboratory of Computer and Information Science, IEEE Transactions on Neural Networks, Vol. 10, No. 3, 1999, pp. 626-634.
16. Yajun Ma and Shexiang Ma , “An Improved Fast ICA Algorithm for Signal Separation of Satellite–Based AIS,” International Conference on Information and Communications Technologies (ICT 2014), 2014 .
17. Aapo Hyvtirinen ,Juha Karhunen, and Erkki Oja, Independent Component Analysis, Wiley, New York,2001.
18. http://pes.edu/cori/projects/space-based-automatic-identification-system/