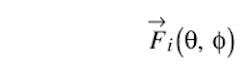Multiple Antennas Arm Effective MIMO Systems

Capacity is critical for the profitability of larger wireless networks, and multiple-input-multiple-output (MIMO) systems provide potentially high capacity.¹ These systems use multiple antenna elements in both the transmitter and receiver to improve the capacity over single antenna topologies when operated in multipath environment. The properties of these antennas play key roles in determining the overall system performance. And, in spite of the number of studies on MIMO systems, little has been reported on successful implementation and optimization of multiple antennas in a mobile telephone. What follows is a review of methods by which an antenna designer can evaluate the MIMO performance of mobile-telephone antennas in terms of channel capacity, capacity versus signal-to-noise-ratio (SNR). This study will also consider the capacity for MIMO systems with an unequal numbers of antennas in the link ends, and the impact of the antenna element properties on the MIMO system performance.

Early work in MIMO antenna elements includes the pioneering studies of Winters², Forschini³, and Telatar.⁴ The basic concept in a receive diversity system is to overcome multipath effects by arming the receiver with multiple versions of the transmitted signal, using distinct channels for each. Since the fading characteristics of each channel tend to be different, a simultaneous deep fade in all of the channels would be rare,¹ providing the receiver with at least one channel with good signal strength. By using spatial, polarization, or pattern diversity, the performance of a wireless system can thus be improved. This means that the signals on the two antennas (with different position, polarization, or radiation patterns) are combined such that fading is avoided in the combined signal. This corresponds to an increase in the SNR in the fading dips, and hence the fading margins in the system link budget can be reduced. Alternatively, the increased SNR can be used to increase the capacity of the communication channel. If two or more antennas are used on both the transmitter and the receiver side, and if the improved SNR is used to increase the capacity of the communication system, a MIMO system is obtained.^5-8

The idea behind MIMO is that the signals on the transmit antennas at one end and the receive antennas at the other end are "combined" in such a way that the quality in terms of the bit-error rate (BER) or the data rate (in terms of b/s) for each of the MIMO user can be improved.⁵ A MIMO system transmits data over a matrix channel rather than just over a single radio channel. This requires signal processing over both time and space (Fig. 1).⁹ The signal to be transmitted is fed to a simplified transmitting block in which proper error correction coding is added, and filtering and amplification is performed. Hereafter, the three different signals are transmitted simultaneously from antenna elements A1, A2, and A3. At the receiver, each of the antenna elements B1, B2, and B3 receives a signal from each of the transmitting antennas.

If the received signals at each of antenna elements B1, B2, and B3 are sufficiently independent, as is typically the case in the presence of a rich multipath environment, it is possible to reconstruct the original transmitted signal. The relationship between A_i(t), i = 1,2,3 and B_i(t), i = 1,2,3 is B(t) = H(t) A(t). Each matrix H represents the transmission at a certain time (t) and spatial location of the antennas in the multipath environment. Hence, a (3, 3) MIMO system, with three receive and three transmit antenna elements, has a potential capacity increase of three as compared to a single-element system. In an ideal multipath channel, this yields an upper theoretical MIMO capacity that is linear with the number of antenna elements N in a (N, N) MIMO system.¹ Compared to a traditional single-input-single-output (SISO) system, there is a linear increase in capacity by the amount m, where m is the smallest of the number of transmit or receive antenna elements.³

In theory this gives an upper speed limit that is limited only by the hardware cost and the requirement of a rich multipath environment. Therefore, MIMO systems are very attractive in order to boost the capacity of a wireless-communication system that operates in a rich multipath environment.

However, in a more practical MIMO system the capacity is reduced due to correlation between the signals in the receiver,¹⁰ this effect has been investigated both theoretically^{11, 12} and experimentally.¹³ Therefore, the correlation between the signals that are received from the different antenna elements is an important parameter in a MIMO system, due to the increased capacity for decreased correlation.⁶ As long as the envelope correlation is less than ρ_e < 0.5 diversity gain could be obtained in a mobile phone.¹ Even though, this motivates for low correlation, it is not a guarantee for high capacity, since in some special propagation scenarios, the MIMO channel capacity can be low (i.e., comparable to the SISO capacity) even though the signals at the antenna elements are uncorrelated.¹⁴ This effect that has been denoted "keyhole" leading to a drop in the capacity.¹⁵ It is related to scenarios where rich scattering around the transmitter and receiver leads to low correlation of the signals, while other propagation effects, like diffraction or wave guiding, lead to a rank reduction of the transfer function matrix. This gives rise to significant local scattering around both the transmitter and the receiver unit causing uncorrelated fading at each end of the MIMO link. However, the channels still have poor rank properties and hence low capacity. The rank of the MIMO channel is defined as the number of independent equations offered by the MIMO system (the algebraic rank).³ The rank is always less than both the number of transmit antennas and the number of receive antennas.

Recently, Oestges et al.¹⁶ found that high correlation does not necessarily result in low capacity. In Schumacher et al.,¹⁷ the physical channel is related to the observed correlations. In both cases, it is the cross correlation that is investigated; in the current work, the correlation between elements will be examined. The results obtained in refs. 16 and 17 are therefore not directly comparable to the results discussed by Thaysen et al.⁶

Moreover, in a lean scattering environment with mostly line-of-sight properties, a simple receiver diversity system will yield full transmission. However, for a MIMO system, mainly line-of-sight properties cause increased correlation at the receiver, and hence the principle behind the MIMO system collapses since three unknowns must be resolved from a linear system of one equation. By proper handshaking between the receiver and the transmitter, the potential collapse of the MIMO principle can be avoided.³

An expected linear enhancement in capacity with an increase in the number of antenna elements would imply a desire for an increased number of antenna elements. However, mutual coupling between the antenna elements affects the correlation.^18-23 For a finite-sized mobile telephone, the proximity of antenna elements causes inevitably higher mutual coupling.^{24, 25} Therefore, it is necessary to know more about how these antennas should be oriented to minimize the coupling²⁵ and improve the correlation.²⁶ Increased mutual coupling results in higher spatial correlation²⁶ which in many case leads to a lower MIMO gain compared to fully uncorrelated antenna signals.⁹

There are two kinds of antenna correlation: Signal correlation and envelope correlation. Signal correlation refers to the correlation between the complex signals received from two different antennas, while envelope correlation refers to the correlation between signal amplitudes received from two different antennas. Envelope correlation is often the parameter measured in antenna experiments (phase less) and is in most cases approximately equal to the square of the complex magnitude of the signal correlation.²⁷ In Vaughan et al.,²⁷ the maximum relative error is computed to being less than 10 percent. In the present work, unless otherwise mentioned, reference is to the correlation that is calculated using the complex value of the signals.

Page Title

The calculation of the antenna correlation can be approached in different ways, one is based on the far-field pattern,¹ and another is based directly on the scattering parameters at the antenna terminals.²⁸ A third method based on Clarke's formula²⁹ has recently been used by Boyle³⁰ and Hui et al.³¹ Performing correlation calculations using the radiation pattern principle can be time consuming, independent of whether it is done using numerical or experimental data. However, it is an often-used method (see for example, ref. 32). Blanch et al.²⁸ proposed a formula for calculating the correlation between antennas in a two-antenna system using scattering parameters. The results coincide with those obtained from radiation-pattern measurements of each of the elements. The correlation between two antennas can be calculated using the impedance matrix as well.³³

Thaysen et al.⁶ proposed a novel closed-formed expression for calculating the envelope correlation coefficient from the scattering parameters between any two antennas in a (3, 3) MIMO antenna array system. The expression provides knowledge of where effort should be placed in antenna design and optimization for antennas in a diversity or MIMO system.

In Thaysen et al.,⁶ a (3, 3) MIMO system was created, thus the correlation between any two antennas in this three-antenna system is required. The formula was derived using the law of energy conservation,³⁴ also the case in work by Blanch et al.²⁸ and Salonen et al.³⁵ The envelope correlation for a two-antenna system can be calculated using Eq. 1, ^{11, 27, 28} where:

is the field radiation pattern of the antenna system when port i is excited (all other ports are terminated with loads representing the source impedance on their ports), and • denotes the Hermitian product.

In the case of a (3, 3) MIMO system, with N = 3 antenna elements in both the receive and transmit ends, the envelope correlation between antenna i = 1 and j = 2 could be calculated using Eq. 2. For the correlation in a two-antenna diversity scheme, i.e., N = 2:(Eq. 2)²⁸

Further details regarding the derivation are presented in ref. 6.

Thaysen et al.⁷ extended the envelope correlation formula to the general (N, N) case (also valid for the two- and three-antenna systems, i.e., N = 2 and 3). Hence, the closed formed equation for the magnitude square of the complex correlation (which is the same as the power correlation) and approximately equal to the envelope correlation²⁷ between any two antennas in a MIMO system consisting of N antennas was derived as:⁷

The envelope correlation is determined from the distribution of the external sources and the radiation pattern from the antennas. By assuming an omni-directional source distribution, it is possible to relate the mutual impedances (or scattering parameters) to the correlation.²⁷ This means that the envelope correlations estimated based on S-parameters (Eq. 3) correspond to that given by Eq. 1 only if a uniform distribution of the sources is assumed. Given that the investigation is to design practical antenna system for MIMO (e.g., in a mobile telephone), the uniform distribution of the sources assumed in the envelope correlation expression may be inadequate. Therefore, it should be clearly pointed out that this formulation cannot completely replace the correlation, calculated using Eq. 1 (as a quality criterion) in the case of small terminal antennas. The radiation-pattern-based method gives the possibility to include a better description of the radio channel in the evaluation, although it makes the evaluation more cumbersome. However, it is found that the envelope correlation calculated using the scattering parameters yields sufficiently accurate results, and thus could be used in many practical cases.

Thaysen et al.⁷ validated the proposed formula in the special case of a (3, 3) MIMO system by comparing the envelope correlation obtained with Eq. 1 to that based on Eq. 3 (Fig. 2). From 1.4 to 2.4 GHz, the envelope correlation calculation based on Eq. 1 yields slightly lower values compared to the radiation-pattern-based method of Eq. 3. The difference in part could be caused by the measurement facility, mainly the dips in the radiation patterns in the region where φ= 180° ± 12°, (see ref. 6) which are caused by the antenna mounting and positioning system.³⁶ The discrepancies can also be attributed to the fact that the scattering parameters are measured in the laboratory, whereas the radiation patterns are measured in an anechoic environment.

The maximum absolute difference between the envelope correlations of Eq. 1 and those based on Eq. 6 are 0.04. An error of 0.04 is small compared to the 0.5 diversity rule of thumb (i.e., less than 10-percent error). Even though the radiation efficiency is as low as 80 percent for antenna 3, the discrepancies are still very low, meaning that the proposed formula could be used in many cases even though the loss is not included in the scattering parameter formula.

This ends part 1. Next month, the conclusion of this two-part article on MIMO antennas will present the results of studies based on 15 different two-antenna configurations, showing the importance of antenna location and orientation in systems where envelope correlation is essential. The authors will show the optimum MIMO antenna configurations for achieving maximum capacity in comparison to alternatives based on antenna diversity techniques.

Page Title

ACKNOWLEDGMENTS
This work was supported by Nokia Denmark. The authors wish to thank Elna Sorensen from Technical University of Denmark for proofreading the article. Thanks are also due for valuable comments from Kimmo Kalliola from Nokia Research Centre, Helsinki, Pasi Suvikunnen and Dr. Petri Vainikainen from Helsinki University of Technology, Dr. Jorgen Bach Andersen from Aalborg University, and Dr. Erik Bruun from Technical University of Denmark.

REFERENCES

1. R.G. Vaughan and J. Bach Andersen, "Antenna diversity in mobile communication," IEEE Transactions of Vehicular Journal of Technology, Vol. 36, pp. 149-172, 1987.
2. J.H. Winters, "On the capacity of radio communication systems with diversity in a Rayleigh fading environment," IEEE Journal on Selected Areas in Communications, Vol. SAC-5, pp. 871–878, 1987.
3. G.J. Foschini and M.J. Gans, "On limits of wireless communications in a fading environment when using multiple antennas," Wireless Personal Communications, Vol. 6, pp. 311–335, 1998.
4. I.E. Telatar, "Capacity of multi-antenna Gaussian channels," European Transactions on Telecommunications and Related Technologies, Vol. 10, pp. 585–595, 1999.
5. D. Gesbert, M. Shafi, D.S. Shiu, P.J. Smith, and A. Naguib, "From theory to practice: An overview of MIMO space-time coded wireless systems," IEEE Journal on Selected Areas in Communications, Vol. 21 (3), 2003.
6. J. Thaysen and K.B. Jakobsen, "Reduction of antenna correlation for increased MIMO channel capacity"" submitted 2005.
7. J. Thaysen and K.B. Jakobsen, "Envelope Correlation in (N, N) MIMO antenna Array from scattering parameters," submitted 2005.
8. J. Thaysen and K.B. Jakobsen, "An experimental evaluation of the capacity, correlation, efficiency, and mutual coupling of three MIMO designs for mobile phones," accepted for IEEE Transaction on Vehicular Communications, 2005.
9. A. Goldsmith, S. Jafar, N. Jindal, and S. Vishwanath, "Capacity limits of MIMO channels," IEEE Journal on Selected Areas in Communications, Vol. 21, no. 5, pp. 684-702, 2003.
10. R. Janaswamy, "Effect of Element Mutual Coupling on the Capacity of Fixed Length Linear Arrays," IEEE Antennas and Wireless Propagation Letters, Vol. 1, pp. 157-160, 2002.
11. D. Shiu, G.J. Foschini, M.J. Gans, and J.M. Kahn, "Fading correlation and its effect on the capacity of multi-element antenna systems," IEEE Transactions on Communications, Vol. 48, pp. 502–513, 2000.
12. C.N. Chuah, D.N.C. Tse, J.M. Kahn, and R.A. Valenzuela, "Capacity scaling in MIMO wireless systems under correlated fading," IEEE Transactions on Information Theory, Vol. 48, pp. 637–650, 2002.
13. A.F. Molisch, M. Steinbauer, M. Toeltsch, E. Bonek, and R.S. Thomas, "Capacity of MIMO systems based on measured wireless channels," IEEE Journal on Selected Areas in Communications, Vol. 20, pp. 561–569, 2002.
14. D. Gesbert, H. Belcskei, D.A. Gore, and A.J. Paulraj, "Mimo wireless channels: Capacity and performance prediction," in Proc. IEEE Globecom 2000, San Francisco, CA, pp. 10831088, Nov. 2000.
15. D. Chizhik, G.J. Foschini, M.J. Gans, and R.A. Valenzuela, "Keyholes, correlations, and capacities of multielement transmit and receive antennas," IEEE Transactions on Communications, Vol. 1, pp. 361–368, 2002.
16. C. Oestges and A. Paulraj, "Beneficial impact of channel correlations on MIMO capacity," Electronics Letters, Vol. 40, pp. 606–608, 2004.
17. L. Schumacher, K.I. Pedersen, and P.E. Mogensen, "From antenna spacings to theoretical capacities - guidelines for simulating MIMO systems," The 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Vol. 2, pp. 587–592, 2002.
18. D. Chizhik, F. Rashid-Farrokhi, J. Ling, and A. Lozano, "Effect of antenna separation on the capacity of BLAST in correlated channels," IEEE Communications Letters, Vol. 4, No. 11, pp. 337–339, 2000.
19. A. Derneryd and G. Kristensson, "Signal correlation including antenna coupling," Electronics Letters, Vol. 40, No. 3, pp. 157–158, 2004.
20. M. Karaboikis, C. Soras, G. Tsachtsiris, and V. Makios, "Compact dual-printed invertedF antenna diversity systems for portable wireless devices," IEEE Antennas Wireless Propagation Letters, Vol. 3, pp. 9–14, 2004.
21. B. Clerckx, D. Vanhoenacker-Janvier, C. Oestges, and L. Vandendorpe, "Mutual coupling effects on the channel capacity and the space-time processing of MIMO communication systems," Proceedings of the IEEE International Conference on Communication, ICC '03 International Conference, Vol. 4, pp. 2638–2642, 2003.
22. J.W. Wallace and M.A. Jensen, "The Capacity of MIMO wireless systems with mutual coupling," Proceedings of the IEEE Vehicular Technology Conference, pp. 696–700, 2002.
23. J. Thaysen and K.B. Jakobsen, "MIMO channel capacity versus mutual coupling in multi antenna element system," Antenna Measurement Techniques Association, 26th Annual Meeting & Symposium, Atlanta, GA, pp. 124–129, 2004.
24. O. Edvardsson, "Can two antennas be smaller than one?" Proceedings ICAP 2001, pp. 533–536, 2001.
25. J. Thaysen, "Mutual Coupling Between Two Identical Planar Inverted-F Antennas," Proceedings of the IEEE Antennas and Propagation Society International Symposium, Vol. 4, pp. 504–507, 2002.
26. J. Thaysen and K. B. Jakobsen, "Correlation and Coupling Reduction Between Cellular MIMO Antennas," Accepted ETT-European Transactions on Telecommunications, 2005.
27. R.G. Vaughan and J. Bach Andersen, Channels, Propagation and Antennas for Mobile Communications, IEE, ISBN 0 85296 084 0, 2003.
28. J. Blanch, J. Romeu, and I. Corbella, "Exact representation of antenna system diversity performance from input parameter description," Electronics Letters, Vol. 39, pp. 705–707, 2003.
29. R.H. Clarke, "A statistical theory of mobile reception," Bell System Technical Journal, pp. 957–1000, 1968.
30. K. Boyle, "Radiation Pattern and Correlation of Closely Spaces Linear Antennas," IEEE Transactions on Antennas and Propagation, Vol. 50, pp. 1162–1165, 2002.
31. H.T. Hui; W.T OwYong, and K.B. Toh, "Signal Correlation Between Two Normal-Mode Helical Antennas for Diversity Reception in a Multipath Environment," IEEE Transactions on Antennas and Propagation, pp. 572–577, 2004.
32. P.S.H. Leather and D. Parson, "Antenna diversity for UHF handportable radio," Electronics Letters, Vol. 39 (13), pp. 946–948, 2003.
33. A. Derneryd and G. Kristensson, "Antenna signal correlation and its relation to the impedance matrix," Electronics Letters, Vol. 40, No. 7, pp. 401–402, 2004.
34. S. Stein, "On cross coupling in multiple-beam antennas," IRE Transactions on Antennas and Propagation, pp. 548–557, 1962.
35. I. Salonen and P. Vainikainen, "Estimation of signal correlation in antenna array," Jina'02 –12eme Journees. Internationales de Nice sur les Antennas, pp. 383–386, 2002.
36. Internet: www.satimo.com