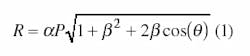Direct digital synthesizers (DDS) are commonly used for sinusoidal signal generation in RF communication systems and test equipment. An integral component of DDS is the digital-to-analog converter (DAC). Although a DAC is intended to perfectly reproduce an analog signal from its digital equivalent, the conversion process is rarely perfect. The DAC's digital resolution (number of bits) is a limiting factor that introduces quantization errors resulting in a noise floor. Other errors, such as linearity errors, create undesired harmonics in the DAC/DDS output spectrum, limiting the spurious-free dynamic range (SFDR). Fortunately, a DDS architecture has been developed that reduces harmonic spurious signals due to the non-ideal characteristics of the DAC, resulting in a significant improvement in SFDR performance.
In general, harmonics can usually be filtered without much difficulty. However, the conversion of a digital signal to an analog signal by a DAC lies in the realm of sampling theory. This means that harmonic signals do not always appear at obvious frequencies according to the rules of digital signal processing (DSP). For example, suppose a DAC sampling at 100 MHz generates a sinusoid with a frequency of 26 MHz. The third harmonic would be expected to appear at 78 MHz where it can be easily filtered. In fact, a third-harmonic image will also appear at 22 MHz because of the effects of sampling. Because it is only 4 MHz away from the fundamental signal, it is difficult to filter without also attenuating the fundamental signal. Obviously, if harmonics could be selectively attenuated, the SFDR performance of the DAC could be improved.
As mentioned earlier, harmonic distortion introduced by the DAC is usually the limiting factor of SFDR performance in a DDS. Present solutions for improving SFDR involve frequency planning and/or the addition of external filtering at the DAC outputs.
An alternative solution is to predistort the digital signal as it arrives at the input to the DAC in such a way that it eliminates the harmonic signal, a technique that is a variation on a method called destructive interference. Summing two sinusoids of the same frequency, but with equal and opposite amplitude, will result in cancellation of both sinusoids.
The mathematical explanation of this concept is best understood by first considering the signals concerned in the context of a DAC-generated sinusoid. The first is the primary sinusoid with amplitude P and frequency wP. An arbitrary spurious signal has amplitude S and frequencywS. The frequencies of the primary and spurious sinusoids are related by wS=NwP (where N>1). Furthermore, in the special case where the spurious sinusoid is harmonic, N is an integer greater than 1. The amplitudes of the primary and spurious sinusoids are related by S = aP, where typically a wS) as the spurious sinusoid is introduced, but offset from the spurious sinusoid by some arbitrary angle q. The amplitudes of the canceling and spurious sinusoids are related by C = bS. However, since the spurious sinusoid and the canceling sinusoid both possess the same frequency, they combine to form a single resultant sinusoid of amplitude R and frequency wS Combining the relationships between the amplitudes of P, S, and C along with the fact that the spurious and cancelling signals are offset by the angle q, it can be shown that the amplitude of the resultant sinusoid (R) is given by:
The most notable feature of this expression occurs when the amplitude of the canceling sinusoid is identical to the amplitude of the spurious sinusoid and phase shifted by 180 deg. This occurs when b = 1 and q = 180 deg. (p rad). Under such conditions, R = 0.
With the above expression for R, it is instructive to examine the quantitative relationship between R, b and q. This is best done by considering the ratio, R/aP, which gives the amplitude of the resultant sinusoid relative to the amplitude of the spurious sinusoid. This ratio, expressed in decibels, is:
Figure 1 demonstrates the way in which R varies as a function of both b and q. The axis labeled "Amplitude Error" equates to b values that deviate from unity over a range of 5 percent. The axis labeled "Phase Error" equates to q values that deviate from 180 deg. over a range of 5 deg. Notice that the four corners of the surface plot are local maxima and register approximately -20 dB. This means that if the phase of the canceling signal is within 5 deg. of being completely out of phase with the spurious signal and is matched to within 5 percent of the amplitude of the spurious signal, then the resultant signal can be expected to achieve a 20 dB amplitude reduction with respect to the level of the original spurious signal.
A basic DDS architecture is comprised of an accumulator, phase-toamplitude converter, and a DAC. This structure is ideally suited for the implementation of the destructive interference concept. A cancellation signal can be generated by adding a duplicate DDS path, excluding the DAC (Fig. 2). However, two modifications must be made to the primary DDS path. The first is the inclusion of an adder inserted between the primary phase-to-amplitude converter and the DAC in order to facilitate the combining of the cancellation signal with the primary signal. The second is a multiplier that has the primary frequency tuning word as one input and a user-specified frequency scaling value as the other input. This provides the ability to adjust the frequency of the cancellation signal. However, because the frequency of the cancellation signal is always an integer multiple of the primary signal (i.e., a harmonic), the design of the multiplier is somewhat simplified (integer rather than floating point).
In addition to the two changes in the primary DDS path, the "cancellation" DDS also requires two modifications (Fig. 2). The first is the insertion of an adder between the accumulator and the input to the phase-to-amplitude converter. This allows the user to apply a phase offset ( ) to the cancellation signal relative to the primary signal. The second is a multiplier between the output of the cancellation phase-to-amplitude converter and the input to the adder that now precedes the DAC. This allows the user to scale the amplitude of the cancellation signal.
Page Title
The ability of the DDS to produce precise integer multiples of the primary frequency is key to the concept of destructive interference. The cancellation DDS can be designed with less complexity than the primary DDS, because the harmonic spurious signals generated by the DAC are usually very small compared to the primary signal. Typically, harmonic spurs are -50 dBc or smaller. This represents a cancellation signal that is no more than 0.32 percent of the DAC fullscale output, which means the upper 8 b of the DAC range are not required for generating the cancellation sinusoid. Thus, if the primary DDS is designed with a 14-b DAC, the cancellation DDS need only be designed with a 6-b output (the 14-b DAC resolution less the 8 unused most significant bits). This, in turn, implies that the phase-to-amplitude converter of the cancellation DDS only requires phase resolution of 9 b. This is based on the "rule of thumb" for DDS design, which states that the phase resolution of the phase-to-amplitude converter must be at least 3 b more than its amplitude resolution in order to maintain 0.5 LSB amplitude accuracy. Thus, the reduced amplitude requirement for the cancellation DDS means that the cancellation DDS requires much less hardware than the primary DDS.
The cancellation DDS can be further simplified. The cancellation DDS makes use of a multiplier prior to the accumulator in order to generate the desired harmonic frequency. However, since an accumulator is nothing more that a recursive adding structure, and multiplication is commutative over addition, then the multiplier can be placed after the accumulator instead of before it. Since the primary and cancellation accumulators operate in parallel, the cancellation accumulator is redundant. This leads to a simpler cancellation DDS as shown in Fig. 3. Figure 3 also shows the reduced complexity of the phase-to-always amplitude converter by identifying smaller input and output data bus widths (Q and S, respectively).
One small problem has been ignored to this point. When the primary and cancellation signals are summed prior to the DAC, an overflow condition will exist. This is because the phase-to-amplitude converter of the primary DDS generates a full-scale sinusoid by design. Any signal added to the full-scale output of the primary phase-to-amplitude converter will necessarily cause an overflow. This is easily prevented by slightly attenuating the output of the primary phase-to-amplitude converter to create enough headroom for the cancellation signal (Fig. 4).
The amount of required attenuation depends on the largest cancellation signal that can be generated by the cancellation DDS. The largest cancellation signal is based on S (the data bus width at the output of the cancellation phaseto-amplitude converter). Given a D-bit DAC and an S-bit maximum cancellation signal, the required attenuation value is given by the formula below. For example, given a 12-b DAC and a 4-b maximum cancellation signal, the attenuation value is 1-2(4-12)=0.99609375:
Extending this concept to a multichannel harmonic suppression technique by replicating the "simplified cancellation DDS" from Fig. 2 is quite simple. This concept is shown in Fig. 5. Note that each cancellation DDS has its own frequency, phase, and amplitude control. All of the cancellation channels sum with the primary signal prior to the DAC.
The only caveat to the multichannel implementation is that the attenuation value for the headroom adjustment must take into consideration the number of cancellation channels (N). This results in a slightly modified version of the attenuation formula:
The actual amplitude and phase values required to destructively interfere with a harmonic spur depend upon the frequency of the primary sinusoid and any internal nonlinearities of the DAC. Due to this variability, the amplitude and phase settings for the cancellation DDS must be determined empirically.
To cancel a harmonic spur, first its actual frequency must be determined. Recall that the effects of sampling may position a harmonic spur at a frequency other than its expected harmonic position. Its actual frequency location can be determined by the following procedure. First, let fS be the sample rate of the DAC, fp the frequency of the primary sinusoid, fH the harmonic frequency, and fSPUR be the frequency of the harmonic spur after correcting for the effects of sampling. To find fH multiply fp by the harmonic number, N (i.e., N = 2 for the 2nd harmonic, N = 3 for the 3rd harmonic, etc.). Next, find the remainder, R, after dividing fH by fS. If R S/2, then fSPUR = R, otherwise fSPUR = fS- R.
With knowledge of the harmonics spur's actual frequency location a spectrum analyzer can be used to determine its amplitude relative to the primary sinusoid. This is done by first noting that the spur magnitude relative to the primary magnitude is measured in units of dBc. For example, if the primary registers -12dB on the spectrum analyzer and the spur measures -71 dB, then the dBc value is -71 - (-12) = -59 dBc. Hence, the voltage relationship between the spur and the primary is:
Since the voltage level of the primary is directly related to the full-scale range of the DAC, then the above ratio should define the range of the required cancellation signal. However, the magnitude of a sinusoid generated by a DAC depends on its frequency. This frequency dependency is deterministic and is defined by the well-known sin(x)/x (or sinc) magnitude response. Since the cancellation sinusoid is generated at the input to the DAC, its amplitude must be scaled to compensate for the sinc response of the DAC. The required scale factor is:
So, the required cancellation amplitude relative to the full scale input of the DAC is given by the formula below. This quantity represents the fraction of the full-scale input of the DAC necessary to produce a cancellation sinusoid of the appropriate amplitude.
The actual amplitude adjustment code, ASCALE(Fig.5), depends on the DAC resolution (D bits) and the cancellation DDS resolution (S bits). Once the appropriate amplitude code is entered, the spur and cancellation amplitudes should be fairly well matched.
Although a spectrum analyzer can help in the determination of the ASCALE value, it cannot help with the value, because a spectrum analyzer cannot measure phase. The determination of the q value requires a trial-and-error approach in order to close in on the proper phase code for the cancellation DDS.
A future installment on this article will examine performance results using the AD9912, a new 1-GSamples/s DDS with two spurious reduction channels. The average spurious suppression will be shown based on slight part-to-part variability. Stability concerns over supply and temperature will also be addressed. Analog Devices, Inc., 804 Woburn St., Wilmington, MA 01887; (800) ANALOGD, FAX: (781) 937-1021, Internet: www.analog.com.
FOR FURTHER READING
- Roger Huntley, Jr. et al., Synthesizer Structures and Methods That Reduce Spurious Signals, United States Patent No. 7,026,846 B1 April 11, 2006.
- DDS Tutorial, http://www.analog.com/UploadedFiles/Tutorials/450968421DDS_Tutorial_rev12-2-99.pdf.