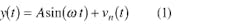Timing jitter and noise are among the least understood engineering concepts, yet they are among the most critical parameters in analog and digital designs. Especially in high-speed communications systems, poor jitter performance can cause increased bit-error rates and limit the system speed. Among the many factors that can influence timing jitter, this article will focus on the effects of random noise.
Timing jitter is generally defined as the short-term variation of a significant instant of a digital signal from its ideal position in time. There are a number of factors that contribute to random timing jitter, including broadband noise, phase noise, spurious signals, slew rate, and bandwidth. Both phase and broadband noise are random, whereas spurious signals are deterministic responses caused by various identifiable interference signals, such as crosstalk and power supply coupling. Slew rate and bandwidth also affect jitter. Figure 1 shows a nonideal sinusoid that contains the three noise sources; in a digital clock signal, these sources contribute to jitter that accumulates over time.
All electronic components, especially amplifiers and logic devices, generate broadband noise. Also known as the noise floor, broadband noise is a combination of shot noise and thermal noise. Commonly found in diodes and transistors, shot noise is caused by random hopping of charges across a potential barrier within a semiconductor junction. Thermal noise, on the other hand, is unaffected by current flow. It is caused by the random thermal motion of carriers, for example within a MOSFET's gate and channel resistance. The thermal noise power is directly proportional to the resistance and temperature.
The effect of broadband noise on timing jitter becomes significant as the operating bandwidth of modern components pushes into the multi-GHz range. For example, a broadband amplifier driver with 40-GHz bandwidth, 10-dB noise figure, 20-dB small-signal gain, and 0-dBm output power generates a 38-dBm noise output 10(40 GHz)>. This results in a signal-to-noise ratio (SNR) of 38 dB. At this SNR level, the broadband noise is a significant contributor to timing jitter. The total root-mean-square (RMS) noise voltage is the integral of the noise floor over the bandwidth.
Figure 2 illustrates how RMS noise is translated into timing jitter.
A sinusoid containing broadband white noise can be represented by:
where:
A = the amplitude,
ω = the angular frequency, andvn(t) = the noise voltage at time t.
The random noise vn(t) has a Gaussian (normal) distribution. The probability distribution f(vn) of the noise voltage vn is:
where:
vnRMS = the RMS noise voltage.
To understand how noise voltage is translated into timing jitter, consider applying y(t) into the input of a jitter-measuring instrument, such as a sampling oscilloscope with a histogram function. Each time y(t) crosses the 0-V threshold, a data point is added to the histogram. Just as depicted in Fig. 2, at time Δt, there is a probability that the noisy signal Δy will reach the threshold; thus the jitter is added to the histogram at Δt sooner or later than the anticipated sampling point. The probability density as a function of the timing jitter Δt is calculated by setting vn = Δy = Asin(2πfΔt) in Eq. 2. The result is the jitter distribution function shown in the histogram.
Equation 3 can be simplified by assuming that Δt is small when compared to the period of the sinusoid; therefore, A sin(2πfΔt) ≅ A(2πΔt) = AωΔt:
Equation 3 then becomes:
Dividing the numerators and denominators of various terms within Eq. 4 by Aω yields:
Equation 5 is a jitter distribution function similar to the Gaussian distribution shown in Eq. 2, except for the scale factor 1/Aω. Thus, the RMS jitter is found as:
The test setup shown in Fig. 3 was used to verify Eq. 6. Both a clean sinusoid and a broadband noise signal were combined and injected into a sampling oscilloscope where jitter was measured at the zero crossing. To ensure meaningful results, the input broadband noise was set higher than the noise floor of the oscilloscope. Figures 4 and 5 show the results of the experiment. Figure 4 shows jitter as a function of frequency with constant RMS noise injected, while Fig. 5 shows jitter as a function of RMS noise voltage with constant frequency. The similarity between the measured and calculated jitter curves proves that Eq. 6 can be used to translate broadband noise into timing jitter.
With slight modification, Eq. 6 can also accommodate the jitter translation of other waveforms. By definition, the Aω term of Eq. 6 is the slew rate S at the 0-V threshold. Any waveforms with a known slew rate at the threshold can be used to relate Δt to Δy, because vn = Δy = S Δt (see Fig. 2). Substituting this into Eq. 2 yields Eq. 7:
Dividing the numerators and denominators of various terms within Eq. 7 by S yields:
Equation 8 is similar to the Gaussian distribution shown in Eq. 2 except for the scale factor of 1/S. Thus, the RMS jitter is:
The test setup shown in Fig. 3 was again used to verify Eq. 9. The sinusoid was replaced by a variable-slew-rate square wave. Jitter was measured at the 50-percent point of the rising edge of the square wave.
The results of those measurements (not shown) raise an interesting point. It appears that a faster slew rate waveform results in lower jitter. However, a faster slew rate requires a higher operating bandwidth, which increases the RMS noise of the system. The RMS noise is directly proportional to the bandwidth. With this relationship in mind, system designers must carefully choose the slew rate and bandwidth to minimize jitter.
Page Title
Phase noise is present in every active and resistive component, but it is most severe in oscillators. These oscillators include free-running crystal oscillators and phase-locked oscillators in clock-recovery applications. Phase noise is a specification that characterizes spectral purity. For example, an oscillator output should ideally be a pure sinusoid represented as a vertical line, stationed on a single frequency, in the frequency domain. However, in reality, there are noise sources in the oscillator that can cause the output frequency to deviate from its ideal position, thus generating a "skirt" of other frequencies near the carrier (fundamental) frequency. Referred to as phase noise, these frequencies result from the noise sources modulating the oscillator. They often appear above the noise floor and close to the carrier frequency. Phase noise is usually specified as the ratio of a noise power at an offset frequency away from the carrier to the carrier power, in a 1-Hz bandwidth. Because noise sources frequency-modulate the signal to produce phase noise, phase noise is unaffected by the slew rate.
Due to the limitations of most jitter-measuring equipment, it is often easier to characterize the purity of a low noise signal by measuring its phase noise in the frequency domain rather than measuring jitter in the time domain. For example, most jitter-measuring oscilloscopes are only capable of measuring jitters down to 1 ps RMS. Most modern real-time oscilloscopes only have bandwidths to 7 GHz. Phase-noise test equipment, on the other hand, can measure noise levels of the best low-noise oscillators available (much less than 1 ps in the time domain) and offer bandwidths of to 40 GHz.
The translation between phase noise and timing jitter has been explored in previous articles.1,2 To derive the necessary equations relating phase noise to jitter, consider Eq. 10 as a sinusoid containing phase noise:
where:
A = the amplitude,
fo = the nominal frequency, and
φ(t) = the phase noise.
Jitter is commonly measured at the 0-V crossing between two or more periods. At the 0-V crossing, the terms inside the parentheses of Eq. 10 is 2πN,
where:
t1 = the first zero-crossing and
t2 = the Nth zero-crossing.
Subtracting the two equations yields
The time between the two zero-crossings is the number of periods plus the jitter
where:
T0 = the period or 1/f0 and
Δt = the jitter accumulated after N periods.
Substituting Eq. 14 into Eq. 13 yields Eq. 15. Rearranging Eq. 15 and cancelling out the 2πN terms yields jitter, Eq. 16. The squared RMS jitter is given by Eq. 17. Because φ(t) is a stationary process, Eq. 18 results.
where:
Sφ(f) = the spectral density of φ(f) and f = the offset (Fourier) frequency.
The middle term of Eq. 17 then becomes Eq. 19, where:
Rφ(τ) = the autocorrelation function of φ(f) and τ ≅ NTo = the time after the Nth period.
The squared RMS jitter after the Nth period at time τ can be calculated by Eq. 20.
Recalling the algebraic identity 1 cos(2πfτ) = 2 sin2(πfτ) and assuming the phase noise is close to the carrier and symmetrical, meaning the integration from fOFFSET to 0 equals the integration from 0 to +fOFFSET, Eq. 20 can be rewritten as Eq. 21.
Term Sφ(f) is approximately equal to the phase noise L(f) for close-in phase noise3; that is, the Fourier offset frequency is much less than the carrier frequency: fOFFSET << fO and Eq. 22 results.
A phase-modulating circuit4 was used as part of the test setup shown in Fig. 6 to verify Eq. 22. The phase-modulating circuit provides a convenient way to produce a variable phase-noise signal that is free of spurious content. The output of the circuit was first measured for timing jitter with a sampling oscilloscope, and then measured for phase noise with a spectrum analyzer (not shown). The phase-noise profile of the circuit is similar to the noise profile of a phase-locked oscillator, where the phase noise is constant inside the loop bandwidth and rolls off outside the bandwidth. Using numerical integration to integrate Eq. 22, the resulting accumulated-jitter with respect to period was plotted in Fig. 8, which confirms the validity of Eq. 22.
Spurious signals also contribute to timing jitter, especially in oscillators. Spurious signals are caused by phase-locked-loop (PLL) reference spurious products, power-supply coupling, crosstalk from nearby circuitry, and other sources. As shown in Fig. 1, these spurious products usually appear as small spikes near the carrier frequency. Equation 22 can help relate spurious signals to timing jitter. Because spurious signals only occur at specific frequencies, the integration function in Eq. 22 can be replaced with Eq. 23.
Since Eq. 23 does not assume that the spurs are symmetrical, it is multiplied by a factor of 4 instead of 8. The spurious products on both sides of the carrier must be included in the jitter calculation. L(fn) is the spurious amplitude relative to the carrier (the desired signal) and is usually given in dBc. Parameter fn is the offset frequency of the nth spurious product. Figure 7 shows the plot of Eq. 23 using a spurious product on both sides of the carrier at 100 kHz offset and an amplitude of 40 dBc. Reference 1 verifies Eq. 23 by modulating a voltage-controlled crystal oscillator with a sinusoid to produce a spurious product on each side of the carrier (not shown).
Broadband noise, phase noise, and spurious products are the three contributors to timing jitter. Broadband noise is purely random and uncorrelated, thus the jitter it produces does not accumulate. The latter two, however, generally do produce accumulating jitter. The squared total timing jitter is the sum of the three squared jitters. The noise-floor jitter term is calculated from Eq. 9, the phase-noise jitter term is calculated from Eq. 22, and the spur jitter term of Eq. 24 can be calculated from Eq. 23.
The correlation between the experimental and calculated data demonstrates the relationship between the three major noise sources and timing jitter. Designers of high-speed systems can use Eqs. 9, 22, and 23 to translate noise into timing jitter.
REFERENCES
1. Ali Hajimiri et al., "Jitter and Phase Noise in Ring Oscillators," IEEE Journal of Solid-State Circuits, Vol. 34, No. 6, pp. 790-804.
2. Boris Drakhlis, "Calculate Oscillator Jitter By Using Phase-Noise Analysis," Microwaves & RF, January 2001 pp. 82-90 and p. 157.
3. W.F. Egan, Frequency Synthesis by Phase Lock, Wiley, New York, 1981.
4. Enrico Rubiola et al., "The ±45(infinity) Correlation Interferometer as a Means to Measure Phase Noise of Parametric Origin," IEEE Transactions On Instrumentation and Measurement, Vol. 52, No. 1, pp. 182-188.