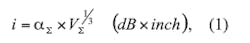Transmission lines are often taken for granted in the design of high-frequency circuits and integrated circuits (ICs), since the focus is often on getting signals into and from an active device. But by understanding the capabilities of different microwave/RF transmission lines and how to optimize them, design iterations, time, and unnecessary cost can be saved from a project. Part 1 of this two-part article will show how a careful design process should include an analysis of requirements through final documentation, allowing a designer to balance such tradeoffs as electrical performance, size, cost, and reliability.
The major parameters that define an RF/microwave design are cost, volume, weight, electrical performance, power, and reliability. Cost, for example, can be controlled through the use of a low-cost technology process, a low-cost substrate material, a simple assembly, low-cost components, minimal interconnections, an effective electrical ground contact with good heat flow and heat sinking, and multilayer construction. Of course, this is not an exhaustive list of guidelines, and cost will also be influences by limitations imposed by such factors as required receiver sensitivity, size, receiver selectivity, and power consumption.
The size and weight of a high tance. For example, suppose that k1 is the cost coefficient, k2 is the volume coefficient, k3 is the weight coefficient, k4 is the electrical performance coefficient, k5 is the supply power coefficient, and k6 is the reliability coefficient. For calculation and optimization, each parameter should be normalized: C/k1, S/k2, W/k3, E/k4, P/ k5, and 1/(Rk6). Then the normalized parameters should be added by using the summation formula shown in Eq. A in the box at the bottom of p. 106. For an optimized transmission line, the combined parameter, Σ, must be minimized.
Figures 2-7 show common planar transmission lines. All printed transmission lines have strip conductor(s) implemented on a relatively thin substrate. Printed transmission lines can be classified as being uniform or nonuniform; homogeneous or inhomogeneous in their surrounding area; lossless or lossy; shielded or nonshielded; planar, multilayer, or threedimensional; and based on different substrate types, including dielectric, ferrite, or semi-insulating materials.
In a uniform line, the characteristic impedance does not vary with position along the line. A nonuniform printed transmission line exhibits characteristic impedance that varies as a function of the longitudinal coordinate. Usually, this change in impedance is achieved by changing the conductor strip width. Tapered transmission lines can be fabricated with smooth changes in conductor width and characteristic impedance as functions of distance along the line.
For transmission lines with inhomogeneous or mixed dielectric, such as a microstrip line (Fig. 2), the velocity of propagation depends on both the cross-sectional geometry of the line and the dielectric constants of the different dielectric media (air and substrate material). The effective dielectric constant of the line can be justly expected to be greater than the dielectric constant (e) of air (e = 1) and less than that of the dielectric substrate material. For this type of transmission line, the propagation of the electromagnetic (EM) waves does not take place in a purely transverse electromagnetic (TEM) manner. Usually, in a low-loss printed transmission line, the conductor thickness is greater than three to five times the skin depth. Lossy transmission lines with conductor thickness significantly less than the skin layer thickness can be used for distributed planar attenuators or terminations.2
For some regular printed transmission lines and combinations of different transmission lines, a multilayer design is necessary. The main objective of a multilayer RF construction is to significantly increase the density of an RF module. Also, a multilayer design provides the opportunity to combine both RF and digital functions in a single module. This provides benefits of size and weight reduction, enhanced performance, improved reliability, and decreased cost. In addition to normal planar interconnections, the interconnections in a multilayer module include vertical transmission lines or via-hole interconnections. In a threedimensional design, the transmission lines make it possible to send signals along orthogonally placed conductors. For an RF network, a three-dimensional or horizontal-vertical design is attractive.1,2 A three-dimensional configuration can consist of various combinations of multilayer, horizontalvertical, and flexible structures.
Typical nonshielded transmission line structures (Figs. 2a, 2c, 2d, 5, 6a, and 6c) are open to the air, so it is usually desirable to protect them from environmental influences, as well as to prevent radiation and electromagnetic interference (EMI). Such protection can be realized by the use of shielded printed transmission lines (Figs. 2b, 3, 4, 6a, and 7).
Selection of a transmission line substrate depends on the technology process. Hybrid microwave integrated circuits (HMIC) use printed transmission lines with dielectric or ferrite substrates. In monolithic microwave integrated circuits (MMICs), the transmission lines are fabricated on a Optimum impedance matching between the transmission line and the interface results in better efficiency in the overall RF network. As Table 2 shows, the impedance range of printed transmission lines is somewhat limited. In terms of electrical performance, the most important parameter of a transmission line is insertion loss, and Table 3 compared the insertion-loss performance for different standard printed transmission lines.
Design tradeoffs usually deal with conflicting parameters, such as insertion loss versus transmission line physical dimensions. Decisions for optimization should be made according to the transmission-line integration index2:
where
aΣ = the total insertion loss of a printed transmission line (in dB) and V = the volume of a transmission line in in.3, VΣ = LΣ x WΣ x H Σ where LΣ , ΣW , and ΣH = the total (equivalent) length, width, and height of a transmission line, respectively.
The transmission line with minimum integration index, imin, is optimal, having the smallest physical dimensions with the minimum insertion loss. Keep in mind that integration index varies linearly with frequency.
The total insertion loss for the printed transmission line is
Using the normalized coefficient, (4LΣ )4/3/?, the normalizedintegration index is
Continue to page 2
Page Title
The best prototype should have a minimum integration index. Consider microstrip and stripline prototypes with different characteristics. There are some limitations of the physical dimensions of these transmission lines. The total (equivalent) width, W = W + (3 - 5)W, is equal to the sum of the conductor width, W, and the EM area (3 - 5)W around the conductor. The total height of a stripline is H = b, where b is the height of the two dielectric substrates. For a shielded microstrip line, HΣ = 7h, where h is the thickness of the dielectric substrate. Tables 4 and 5 represent different parameters (dimensions, loss, normalized integration index for 1 GHz) of microstrip line, shielded microstrip line, and stripline with a substrate dielectric constant of 2.2, substrate dissipation factor of 0.002, and impedance of 50 ohms.
Selection of a transmission-line prototype depends on all requirements, and must take into account the corresponding weighting coefficients. The following procedure is recommended.
First, compare the transmission-line prototype's normalized parameters, Ppr i/Preq i, with the normalized requirements, Preq i/Preq i = 1, and determine the deviations, i = 1 - Ppr i/Preq i for each prototype (from 1 to n). Then, choose the weighting coefficients, ki , for each parameter as described above, with k = 1 for the most important parameter. Following this, normalize parameter deviations with respect to the weighting coefficient for each prototype, by using Δi/ki (for Δi > 0). The next step involves adding all deviations for each prototype by means of the summation:
Then compare the sum of the deviations for the different prototypes from prototype 1 to prototype n and choose the one with the minimum value of summed deviations.
If some of the requirements are not satisfied, it will be necessary to look for modification to the prototype transmission line or a combination of different transmission lines (step 7 in Fig. 1). Table 6 shows which parameters of a transmission line are most relevant for the various requirements, while Table 7 compares the different printed transmission lines.
The final selection of a transmission line prototype can be made by analysis of a circle diagram. Figure 8 shows an example of a circle diagram for two preliminary prototypes: microstrip line (blue) and stripline (brown). The parameters of the two lines are corrected using the weighting coefficients. The optimum prototype should have the minimum area between the real and goal performance targets.
The technology process 2 can be selected according to Table 8. If one process is not satisfactory, a designer can use a combination of different processes.
Substrate materials of RF and microwave print transmission lines may be dielectrics, ferrites, or semiconductors. Selection of the substrate material for a choice of transmission line depends strongly on a particular technology process. The issues with some substrate materials were discussed in detail in ref. 2. A substrate should have the following characteristics: low cost; available with thin height (to reduce size, dispersion, and radiation loss); low dielectric constant (if low cost and reduced effects of tolerance variations are important); high dielectric constant (if small size and low radiation losses are most important, with package size approximately inversely proportional to the square root of the dielectric constant); well controlled substrate thickness and dielectric constant; low dissipation factor; fine surface finish; minimal variation of dielectric constant and dissipation factor with temperature; dimensional stability and uniformity of thickness; high thermal conductivity (especially for high-power designs); and low moisture absorption.
PCB technology is based on the use of copper-laminated plastic substrates. These organic-type plastic materials feature low dielectric constants, have low loss, are easy to machine, and are low in cost. Materials include woven Teflon fiberglass, microfiber Teflon glass, and polyolefin, with dielectric constants between 2.2 and 10.5 (Table 9). Low-temperaturecofired- ceramic (LTCC) technology is based on multiple stacked layers of ceramic material. Dielectric materials most commonly used for thick-film technology are Al2O3 (96 percent), AlN, and BeO. For thin-film technology, typical substrate materials are Al2O3 (99.6 percent), AlN, BeO, and quartz. MMICs are fabricated using semiconductor materials, such as gallium arsenside (GaAs), silicon (Si), and composite semiconductor materials, such as silicon carbide (SiC) and silicon germanium (SiGe).
For an optimum transmission-line design, the selection of conductor materials is an important issue. In most conventional microstrip designs, conductor losses in the strip conductor and the ground plane dominate over dielectric and radiation losses. Conductor losses are a result of several factors, among which are conductivity, skin effect, and surface roughness. With finite conductor conductivity, there is a nonuniform current density starting at the surface and decreasing exponentially into the bulk of the conductive metal. This is the known skin effect. To minimize conductor loss, conductor thickness should be greater than three to five times the skin depth.2 As the roughness of the substrate surface increases, the conductor length of the current path increases, and, therefore, the losses increase.
For PCBs, a variety of dielectric materials with copper cladding (electrodeposited or rolled) on one or both sides of the substrate are available. For thick-film circuits, conductive paste (silver, gold, palladium-gold, and so forth) is used for conductors. Thinfilm technology involves sputtering a metal that has good adhesion to the substrate to form a thin adhesive layer. The next step is sputtering a layer of Au. The DBC process is used for directly bonding a copper sheet to a ceramic or ferrite substrate, after which a transmission line is formed there on by masking and etching.
The effect of tolerances of the transmission line performance can be analyzed using the sensitivity approach.4 For example, change in microstrip impedance values can be evaluated using Eq. C from p. 106, where the term
is the sensitivity of parameter A with respect to parameter B.
The tolerances of a substrate's dielectric constant and thickness are specified by the material's manufacturer. The tolerance of the conductor width depends on the technology process. The dimensional tolerances are most critical for relatively thin substrates or relatively narrow center conductors.
The synthesis of printed transmission lines is based on both system requirements and derived requirements. The synthesis results include the physical dimensions of a transmission line, the substrate performance, and the package performance. Analysis of a printed transmission line entails definition of electrical performance of the printed line with known physical dimensions and substrate material. An EM simulation may be used to create an S-parameter model of a transmission line.
Consider the main restrictions on the physical dimensions of a transmission line. The maximum size of a basic microstrip (Fig. 2a) can be calculated according to the following two rules: the 3-W rule and the 5-h rule. The 3-W rule for trace separation will reduce the crosstalk flux by approximately 70 percent; for a 98-percent reduction in crosstalk between traces, change the 3-W rule to a 10-W rule. The 5-h rule refers to the fact that for shielded microstrip line (Fig, 2b), the total height is H = (5-7)h, where h is the dielectric substrate thickness. When H is greater than (5-7)h, the enclosure effects are negligible.
A microstrip circuit that has been fitted into a housing may be looked upon as a dielectrically loaded cavity resonator (Fig. 2b). The dimensions of this resonator (length, L, width, a, and height, H) should be selected in such a way that the parasitic waveguide modes are below cutoff. The factors that affect the choice of substrate thickness h of the microstrip line are most controversial.2Table 10 offers some of the parameters for microstrip line performance versus substrate thickness for a number of different circuit technologies, including PCB, thick-film, and thin-film technologies. As the substrate material becomes thicker, it becomes more dispersive, which effectively sets an upper limit on the substrate thickness and/or maximum operating frequency.
Next month, in the conclusion of this two-part article, recommendations will be made for choosing the physical dimensions of stripline transmission lines and suspended stripline transmission lines for optimum performance. Part 2 will also explain how matrix representations can be used for analysis of transmission lines in RF and microwave applications. Finally, it will review the role of substrate materials and the thickness of those materials for optimizing the performance of transmission lines when fabricating high-frequency RFICs.
REFERENCES
1. A. Contolatis and V. Socolov, "90 deg RF Vertical Interconnects," Microwave Journal, June 1993, pp.102, 104.
2. Leo G. Maloratsky, Passive RF & Microwave Integrated Circuits, Elsevier, New York, 2003.
3. R. C. Daigle et al., "Multilayer Microwave Boards: Manufacturing and