>> Microwaves & RF Resources
.. >> Library: Article Series
.. .. >> Topic: Phased-Array Antenna Design
.. ... .. >> Phased-Array Antenna Patterns
Download this article in PDF format.
Previously in this series, we introduced the phased-array concept, beamsteering, and array gain. Then we presented the concepts of grating lobes and beam squint. In this final part, we will discuss antenna sidelobes and the effect of tapering across an array.
Tapering is simply the manipulation of the amplitude contribution of an individual element to the overall antenna response. Earlier in the series, no tapering was applied and the first sidelobes were –13 dBc as seen in the figures. Tapering provides a method to reduce antenna sidelobes at some expense to the antenna gain and main-lobe beamwidth. Following an introduction to tapering, we will elaborate on a few points relative to antenna gain.
Fourier Transform: Rect ↔ Sinc
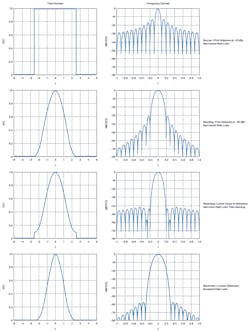
The transformation of a rectangular function in one domain to a sinc function in another domain comes up in different forms in electrical engineering. The most common form is when a rectangular pulse, in time, emits the spectral content of a sinc function. It’s also used in reverse, where wideband applications transform a wideband waveform to a narrow pulse in time. Phased-array antennas have a similar property: a rectangular weighting along the planar axis of the array radiates a pattern following a sinc function.
For applications subjected to this property, the sidelobes of the sinc function are problematic with the first sidelobe being only –13 dBc. Figure 1 illustrates this principle.
Tapering (or Weighting)
A solution to the sidelobe problem is to apply a weighting across the rectangular pulse. This is common in fast Fourier transforms (FFTs), and tapering options in phased arrays are directly analogous to weighting applied in FFTs. The unfortunate drawback of weighting is that sidelobes are reduced at the expense of widening the main lobe. Some example weighting functions are shown in Figure 2.
Waveform vs. Antenna Analogy
The domain transformation from time to frequency is routine enough that it becomes natural for most electrical engineers to visualize. However, for engineers new to phased arrays, how to use the analogy for antenna patterns may not be initially apparent. To do so, we replace the time-domain signal with the field-domain excitation, and the frequency-domain output is replaced with the spatial domain.
Time domain → field domain
- v(t)—voltage as a function of time
- E(x)—field strength as a function of position in the aperture
Frequency domain → spatial domain
- Y(f)—power spectral density as a function of frequency
- G(q)—antenna gain as a function of angle
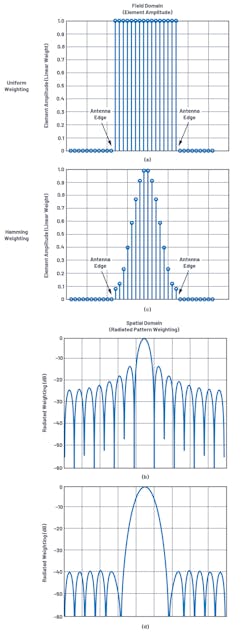
Figure 3 illustrates the principle. Here, we compare the radiated energy for two different weightings applied across the array. Figure 3a and Figure 3c illustrate the field domain. Each dot represents the amplitude of one element in this N = 16 array. Beyond the antenna, there’s no radiated energy, and radiation begins at the antenna edge. In Figure 3a, an abrupt change occurs in the field, while in Figure 3c, there’s a gradual increase with distance from the antenna edge. The resulting impact on the radiated energy is shown in Figure 3b and Figure 3d, respectively.
In the next sections, we will introduce two additional error terms that impact the antenna-pattern performance. The first is mutual coupling. For this article, we merely acknowledge the problem and the amount of electromagnetic modeling used to quantify the impact. The second is quantization sidelobes due to a finite number of bits in the phase-shift control. A more in-depth treatment is given to quantization errors, and quantization sidelobes are quantified.
Mutual Coupling Errors
All of the equations and array-factor plots discussed here assume that the elements are identical, and each has the same radiation pattern. In practice, this isn’t the case. One of the reasons concerns mutual coupling, which is the coupling between adjacent elements. An element’s radiating performance may change significantly when it’s widely separated in the array vs. when it’s spaced more closely. The elements at the edge of the array have a different surrounding environment than the elements in the middle of the array.
Furthermore, as the beam is steered, it changes the mutual coupling between elements. All of these effects create an additional error term to be accounted for by the antenna designer and, in practice, much effort is spent with electromagnetic simulators to characterize the radiation effects under these conditions.
Beam-Angle Resolution and Quantization Sidelobes
Another practical phased-array antenna impairment stems from the finite resolution of the time-delay unit, or phase shifter, used to steer the beam. This is typically digitally controlled with discrete time (or phase) steps. But how does one determine the resolution, or number of bits, required to achieve the beam-quality goals?
Contrary to common misconceptions, beam-angle resolution isn’t equivalent to the resolution of the phase shifters. In Equation 1, we find this relationship:
We can express this in terms of the phase shift across the entire array by substituting the array width D for the element spacing d. If we then substitute the phase shifter ΦLSB for ∆Φ, we can approximate the beam-angle resolution. For a linear array with N elements spaced at a half wavelength, the resolution of the beam angle is shown in Equation 2:
This is the beam-angle resolution off boresight and describes the beam angle when one half of the array has a phase shift of zero, and the other half has a phase shift of the LSB of the phase shifter. Smaller angles are possible if less than one half of the array is programmed to the phase LSB.
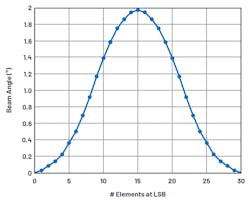
Figure 4 plots the beam angle for a 30-element array using a 2-bit phase shifter, as the phase LSB is progressively switched into elements from left to right across the array. Note that the beam angle increases until half of the elements are shifted by an LSB, and then returns to zero when all elements are at the LSB. This makes sense as the beam angle changes through a difference in phase across the array. Note that the peak of this characteristic is θRES, as previously calculated.
Figure 5 plots θRES as a function of array diameter (at λ/2 element spacing) for different phase-shifter resolutions. This shows that even a very coarse 2-bit phase shifter with a 90° LSB can achieve 1° resolution for an array diameter of 30 elements.
Solving Equation 7 in Part 2 for 30 elements at λ/2 spacing, the main lobe beamwidth is approximately 3.3°, suggesting that we have ample resolution even with this very coarse phase shifter. So, what do we get for a phase shifter offering higher resolution? Drawing from analogies between time-sampled systems (data converters) and space-sampled systems (phased-array antennas), a higher-resolution data converter produces a lower quantization noise floor. Higher-resolution phase/time shifters result in lower quantization sidelobe levels (QSLLs).
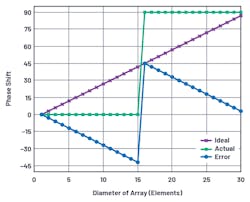
Figure 6 shows the phase-shifter settings and phase error across the 2-bit, 30-element linear array previously described, programmed to the beam resolution angle θRES. Half of the array is set to zero phase shift, and the other half is set to the 90° LSB. Note that the error, the difference between the ideal and actual quantized phase shift, has a sawtooth shape.
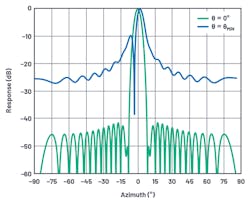
The antenna patterns for the same antenna steered to 0° and to the beam resolution angle are shown in Figure 7. There’s a severe degradation of the pattern due to the quantization error of the phase shifter.
The worst-case quantization sidelobes crop up when the maximum quantization error occurs across the aperture, when every other element is at zero error and the neighbor is at LSB/2. This represents both the maximum possible quantization error and the maximum periodicity of the error across the aperture. This condition is shown for the 2-bit, 30-element case in Figure 8.
Such situations occur at predictable beam angles as presented in Equation 3:
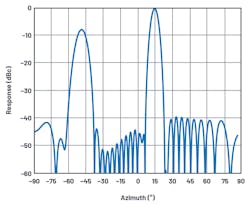
where n < 2BITS, and n is odd. For a 2-bit system, this condition is satisfied four times between horizons, at ±14.5° and ±48.6°. Figure 9 illustrates the antenna pattern for this system for n = 1, q = +14.5°. Note the substantial –7.5 dB quantization sidelobe at –50°.
At beam angles other than the special cases where the quantization error is sequentially 0 and LSB/2, the RMS error is reduced as it is spread across the aperture. In fact, for the angle equation (Equation 3) for even values of n, the quantization error is zero.
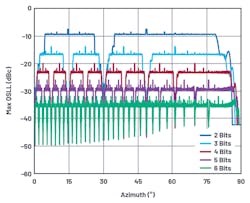
If we plot the relative level of the highest quantization sidelobe for various phase-shifter resolutions, some interesting patterns emerge. Figure 10 shows the worst-case QSLL for a 100-element linear array, employing a Hamming taper so that the quantization sidelobes can be differentiated from the classical windowing sidelobes discussed earlier in this section.
Note that at 30°, all quantization error goes to zero, which can be shown to be a consequence of sin(30°) = 0.5. Notice that the beam angle of the worst-case level for any n-bit phase shifter exhibits zero quantization error at any higher resolution n. The beam angles for worst-case sidelobe levels described here can be seen, as can the 6-dB improvement in QSLL per bit of resolution.
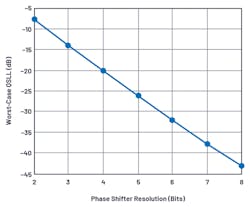
The maximum quantization sidelobe levels, QSLL, for 2-bit to 8-bit phase-shifter resolutions are shown in Figure 11, which follows the familiar quantization-noise law for data converters:
or about 6 dB per bit of resolution. At 2 bits, the QSLL levels are about –7.5 dB, higher than the classical +12 dB for a data converter sampling a random signal. This discrepancy can be viewed as a consequence of the periodically occurring sawtooth error being sampled across the aperture, where the spatial harmonics add in phase. Note that the QSLL isn’t a function of the aperture size.
Closing Comments
We can now summarize some of the challenges faced by antenna engineers relative to beamwidth and sidelobes:
- Angular resolution requires a narrow beam. A narrow beam needs a large aperture, which requires many elements. Furthermore, the beam widens when steered off boresight, so extra elements are needed to maintain the beamwidth as scan angles increase.
- It may seem possible to increase the element spacing to expand the overall antenna area without adding extra elements. This would narrow the beam, but, unfortunately, introduces grating lobes if the elements are uniformly spaced. Reduction of scan angle, along with aperiodic arrays implementing an intentionally randomized element pattern, can be explored to exploit increased antenna area while minimizing the grating-lobe issue.
- Sidelobes are another problem, which we learned can be mitigated by tapering the gain of the array toward the edges. However, tapering comes at the expense of widening the beam, again requiring more elements. Phase-shifter resolution can introduce quantization sidelobes that also must be factored into the antenna design. For antennas implemented with phase shifters, the beam-squint phenomenon causes an angular shift vs. frequency limiting the bandwidth available for a high angular resolution.
This concludes this six-part series on phased-array antenna patterns. We introduced beam pointing, array factor, and antenna gain, then explored imperfections of grating lobes and beam squint. Finally, we discussed tapering and quantization errors. The intention is aimed not for antenna design engineers fluent in electromagnetic and radiating element design, but rather the large number of engineers in adjacent disciplines working on phased arrays who may benefit from an intuitive explanation of the varied impacts affecting overall antenna pattern performance.
Peter Delos is Technical Lead and Bob Broughton is Director of Engineering for Analog Devices' Aerospace and Defense Group, and Jon Kraft is Senior Staff Field Applications Engineer at Analog Devices.
References
Balanis, Constantine A. Antenna Theory, Analysis and Design. Third edition. Wiley, 2005.
Mailloux, Robert J. Phased Array Antenna Handbook. Second edition. Artech House, 2005.
O’Donnell, Robert M. “Radar Systems Engineering: Introduction.” IEEE, June 2012. Skolnik, Merrill. Radar Handbook. Third edition. McGraw Hill, 2008.
>> Microwaves & RF Resources
.. >> Library: Article Series
.. .. >> Topic: Phased-Array Antenna Design
.. ... .. >> Phased-Array Antenna Patterns