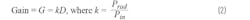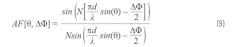Phased-Array Antenna Patterns (Part 2)—Linear-Array Beam Characteristics and Array Factor

>> Microwaves & RF Resources
.. >> Library: Article Series
.. .. >> Topic: Phased-Array Antenna Design
.. ... .. >> Phased-Array Antenna Patterns

Download this article in PDF format.

Part 1 of the series covered beam direction and working with a uniformly spaced linear array of antennas. In part 2, we’ll cover antenna gain, directivity, and aperture, as well as array factors.

Antenna Gain, Directivity, and Aperture

Before we go too far, it’s helpful to define antenna gain, directivity, and aperture. Let’s start with a clarification on gain vs. directivity, as the two are often interchanged. Antenna gain and directivity are in comparison to an isotropic antenna, which is an ideal antenna that radiates evenly in all directions. Directivity compares the maximum power measured, P_max, in a specific direction to the average power radiated across all directions. When no direction is defined, directivity is determined by Equation 1.

Directivity is a useful metric when comparing antennas, because it defines the ability to focus radiated energy. Gain (Equation 2) has the same pattern of directivity, but gain includes the antenna losses:

P_rad is the total power radiated, P_in is the input power to the antenna, and k accounts for losses in the antenna radiation process.

Next, let’s consider an antenna pattern as a function of a 3D direction and directivity as a function of beamwidth (Fig. 1).

The total surface area of a sphere is 4π², and an area on a sphere is defined in units of steradians with 4π steradians in a sphere. Therefore, as shown in Equation 3, the power density from an isotropic radiator is:

and has units of (W/m²).

There are two angular directions for an area of a sphere. In radar systems, these are commonly referred to as azimuth and elevation. Beamwidths can be described as a function of each angular direction using the terms θ1 and θ2: the combination creates an area on the sphere of ΩA.

Ω is the beamwidth in steradians and can be approximated as ΩA ≈ θ1 × θ2.

Recognizing ΩA as an area on the sphere, directivity (Equation 4) can then be expressed as:

The third antenna term we’ll consider is aperture. Antenna aperture represents an effective area for receiving electromagnetic waves and includes a function relative to wavelength. Referring to Equation 5, the aperture of an isotropic antenna is:

Gain is relative to isotropic radiation; as shown in Equation 6, the effective aperture of an antenna is:

Pulling these three terms together, we can see that gain can be considered a function of angle that defines a radiation pattern and accounts for efficiency (or losses) in the antenna.

Array Factor for a Linear Array

At this point, we’re able to predict the optimal time (or phase) delta between elements to achieve maximum antenna directivity. But we’d really like to understand and manipulate the complete antenna-gain pattern. There are two main parts to this pattern (Fig. 2). First, there’s the gain of each individual element of our array (perhaps one patch), called the element factor (GE). Secondly, there’s the impact that we can exert through beamforming the array, called the array factor (GA). The full antenna-gain pattern of the array is the combination of the two factors, as shown in Equation 7:

The GE is the radiating pattern of a single element in the array. This is defined by the geometry and construction of the antenna, and not something that’s varied in operation. It’s important to know because it will limit the gain of our total array—particularly near the horizon. But since we can’t control it electrically, we’ll leave it as a fixed influencer to our total phased-array gain equation. For this article, we’ll assume that all of the individual elements have the same element factor.

The focus then turns to the array factor, GA. The array factor is calculated based on array geometry (d for our uniform linear array) and beam weights (amplitude and phase). Deriving the array factor for a uniform linear array is straightforward, but the details are best covered in the references cited at the end of this article.

There are some variations in equations used across literature depending on how parameters were defined in the linear array. We use the equations from this article, which results in consistency with our definitions in Figures 2 and 3 in Part 1 of this series. Because our primary concern is how the gain changes, it’s often more instructive to plot the normalized array factor relative to unity gain. That normalized array factor can be derived using Equation 8:

where θ₀ = beam angle.

We’ve already defined beam angle θ₀ as a function of phase shift between elements ΔΦ; therefore, we can also express the normalized antenna factor using Equation 9:

The conditions assumed in the array-factor equation include:

• The elements are equally spaced.
• There’s an equal phase shift between elements.
• The elements are all at equal amplitude.

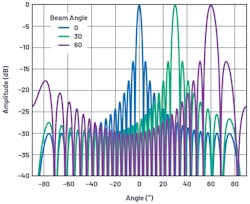
Next, using these equations, we plot the array factor for several array sizes (Figures 3 and 4).

Some observations from these figures include:

The first sidelobe is at –13 dBc regardless of the element count. This is due to the sinc function in the array-factor equation. The sidelobes can be improved by tapering the gain across elements and will be the subject of an upcoming section in this series:

• The beamwidth narrows with the number of elements.
• The beamwidth widens as the beam is scanned away from boresight.
• The number of nulls increases as the number of elements increases.

In Part 3, we’ll cover beamwidth, combining element and array factors, and antenna plots.

Authors’ Note: This series of articles is not intended to create antenna design engineers, but rather to help the engineer working on a subsystem or component used in a phased array to visualize how their effort may impact a phased-array antenna pattern.

Peter Delos is Technical Lead and Bob Broughton is Director of Engineering for Analog Devices' Aerospace and Defense Group, and Jon Kraft is Senior Staff Field Applications Engineer at Analog Devices.

References

Balanis, Constantine A. Antenna Theory: Analysis and Design. Third edition, Wiley, 2005.

Mailloux, Robert J. Phased Array Antenna Handbook. Second edition, Artech House, 2005.

O’Donnell, Robert M. “Radar Systems Engineering: Introduction.” IEEE, June 2012. Skolnik, Merrill. Radar Handbook. Third edition, McGraw-Hill, 2008.

>> Microwaves & RF Resources
.. >> Library: Article Series
.. .. >> Topic: Phased-Array Antenna Design
.. ... .. >> Phased-Array Antenna Patterns