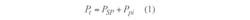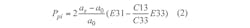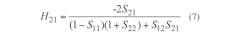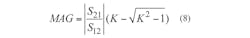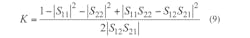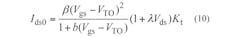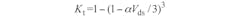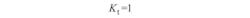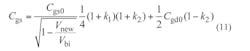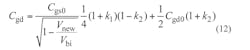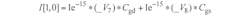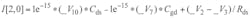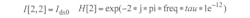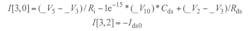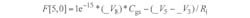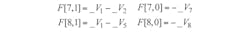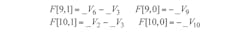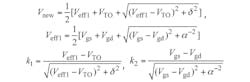Designing AlGaN/GaN HEMTs for W-Band

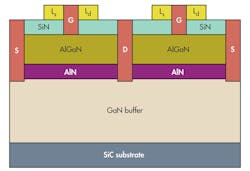
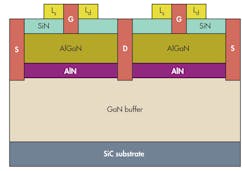
Figure 1 shows the cross-sectional structure of a double-finger AlGaN/GaN HEMT. The gate-length is 0.1 μm and the gate cap is 0.35 μm long. The silicon-nitride (SiN) passivation layer helps reduce surface defects and isolation boost electrode isolation. A single-finger gate width of 50 μm was used based on the principle that the phase difference be no more than π/16 at W-band frequencies. The distance between the source and drain is 2 μm and the lateral structure of the HEMT is symmetric.² This contributes to lower channel series resistance and improved high-frequency characteristics.

The device heterostructure consists of a 1.5-μm-thick GaN buffer layer and a 23-nm-thick AlGaN barrier layer with 24% Al content. To enhance 2DEG channel characteristics, the AlN layer is inserted between the barrier layer and the 1-nm-thick buffer layer. All the vertical layers are unintentionally doped. The 2DEG mobility and sheet carrier concentration are 2000 cm²/V·s and 1.1 × 10¹³ cm^-2, respectively. A silicon-carbide (SiC) substrate was chosen for its excellent thermal conductivity.

The 2DEG of AlGaN/GaN HEMTs is determined by polarization, which is described by Eq. 1:

where P_sp represents spontaneous polarization for the GaN materials and Ppi is the piezoelectric polarization between AlGaN and GaN materials which is given by Eq. 2:

where α, C, and E represent lattice constants, elastic constants, and piezoelectric constants, respectively; their values can be obtained according to the material statement so that polarization can be calculated.³

The channel, regarded as a thin layer, is formed in the buffer layer approaching to surface of the barrier layer because of polarization effect. Empirical fitting function can be used to describe mobility models of the GaN channel.⁴

where T_L and N represent the junction temperature and doping concentration, respectively; and parameters A through F, M1, and M2 are fitting coefficients for the low-field model.

For high-field analysis, the model based on the Monte Carlo method and shown in Eq. 4 has been used:

where E represents electric field. Parameters VSATN, ECN, N1N, N2N, and ANN are fitting coefficients for the high-field model.

The current density of electrons and holes are defined to express change of lattice temperature (Eq. 5):

where q is quantity of electric charge. Parameters μ_n, n, φ_n, and P_n represent electron mobility, concentration, potential, and absolute thermoelectric power, while μ_p, p, φ_p, and P_p are the mobility, concentration, potential, and absolute thermoelectric powers for the semiconductor holes.

The total heat is a result of the sum of the Joule heating term, the recombination and generation heating and cooling term, and the Peltier and Joule-Thomson effects. The expression is described as follows⁵:

where R represents the heating recombination rate and G is the heating generation rate.

The TCAD software was used to simulate the HEMT; all of these physical models will be included in the design procedure. The work function of the gate metal was set 4.8 eV and the SBH can be ensured at 1.5 eV. The background doping concentrations of all the layers were set 10¹⁵ cm^-3. The GaN buffer layer has exhibited high resistance characteristics and the mobility was set at 300 cm²/V·s.

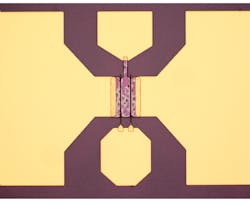
All epitaxial layers were grown on an SiC substrate by means of rapid thermal metal-organic chemical vapor deposition (MOCVD). Ti/Al/Ni/Au is evaporated to form the source and drain electrodes as a result of a rapid thermal anneal at +900°C for 35 s. A transmission-line matrix measurement method determined the ohmic contact resistant at 0.3 Ω-mm. The gate was formed by electronic-beam lithography and Ni/Au was chosen as the gate metal. Figure 2 shows a photo of the device fabricated after fabrication and fabrication process optimization.

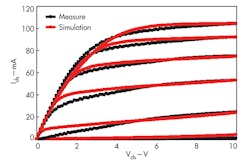
Figure 3 displays measured and simulated curves for I_ds - V_ds for the HEMT structure and device models. The gate voltage was simulated from -5 to 0 VDC and drain voltage from 0 to +10 VDC. The device channel enters the on-state at a gate voltage of -5 VDC, essentially the threshold voltage. The saturation drain current can reach 1.05 A/mm and the knee voltage is 5 V at a 0-VDC gate voltage. This indicates strong depletion-type characteristics for the HEMT device. Measurements indicate a current collapse effect for the HEMT, and further researching will be needed to solve this problem.

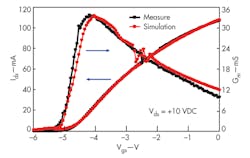
In the meantime, the I_ds - V_gs and G_m - V_gs curves were measured and simulated, and are shown in Fig. 4. When the drain voltage is +10 VDC, the maximum transconductance may reach 338 mS/mm, and this peak value appears at a gate voltage of -4.2 VDC. The measured curves are close to the simulation curves, indicating the validity of the device simulation, and that the TCAD simulation technology is valuable for the design of AlGaN/GaN HEMTs.

The current gain cutoff frequency (f_T) and maximum frequency of oscillation (f_max) are determined by the current gain (H21) and maximum available power gain (MAG), respectively, both calculated by the S-parameters according to Eqs. 7-9:

where K represents the stable factor. The best gate voltage operating point may be determined based on the maximum transconductance. After analysis according to H21 (dB) declining to zero and MAG (dB) declining to zero, f_T) and f_max) can reach 118 and 192 GHz, respectively, at V_gs = -4.2 VDC and V_ds = +10 VDC. With a MAG of 8.2 dB at 75 GHz and 5.7 dB at 100 GHz, this HEMT appears well suited for W-band amplifier applications.

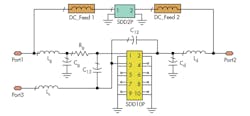
Figure 5 shows a novel SDD large-signal model of the HEMT. It mainly includes a SDD10P section, a SDD2P section, and other electrical components. The SDD10P portion is used to express the intrinsic region while external resistances, capacitances, and inductances are used to express the parasitic parameters, respectively. For high-frequency HEMT devices, it cannot be ignored that the coupling capacitance between the gate and drain (C12) and the coupling capacitance between the gate and source (C13) must accurately fit the high-frequency S-parameters.

In the linear region, 0 < V_ds < 3/α:

In the saturation region, V_ds ≥ 3/α:

where V_TO, β, α, b, and λ represent the threshold voltage, the transconductance, the saturation voltage, the doping tailing factor, and the channel length modulation coefficient, respectively:

where C_gs0 and C_gd0 represent the capacitance between the gate and the source and the capacitance between the gate and the drain, respectively. Parameter δ is the fitting coefficient. For the SDD2P, the port parameters can be described as

I[1,0] = -I_ds + I_ds0 and

I[2,0] = I_ds - I_ds0

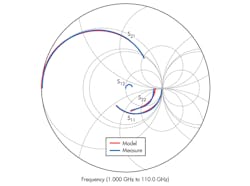
In this case, drain-source current I_ds can express the DC characteristics accurately at different gate and drain voltages. It can still be obtained by using the Statz model. The S-parameters are shown in Fig. 6 by constructing the SDD large-signal model.

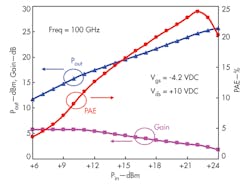
Figure 7 shows output characteristics of the HEMT device at 100 GHz with source and load-pull simulation. According to the maximum power gain match, the linear gain may reach 5.7 dB at small signal state until the input power is +11 dBm. The 1-dB compression point occurs when the input power rises to +15 dBm. The output power is close to +20 dBm and the power-added efficiency (PAE) may reach 16% to the 1-dB compression point. The PAE reaches its highest level when the input power is +22 dBm, a level of approximately 24%. In short, this HEMT represents a good device for higher-frequency monolithic-microwave integrated circuits (MMICs), especially for W-band applications.