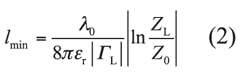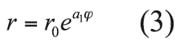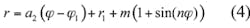Spiral Antenna Cuts Low Profile To 9.4 GHz
This file type includes high resolution graphics and schematics when applicable.
Archimedean spiral antennas (ARSAs) are attractive for a variety of RF and microwave applications. They have been used for circularly polarized broadband communications and can be easily flush mounted in many systems. They are characterized by stable input impedance and radiation characteristics over several octaves. The size of these antennas is determined by the lowest operating frequency, the depth of the cavity, and the length of the feed balun. Many studies have been performed to overcome these size limitations by reducing the aperture1-5 and/or by decreasing the profile6-14 This current report will show how the use of a very short exponentially tapered microstrip balun can lead to a low-profile antenna with impressive bandwidth of 0.8 to 9.4 GHz.
An efficient way to miniaturize the antenna aperture is by meandering the antenna arms,5 which elongates the arms’ electrical length and lowers the operating frequency. Meanwhile, several methods have been proposed to thin the reflectors used to achieve finer unidirectional properties, but without considering the length of feeding balun.14
As an ultrawideband (UWB) feed structure, an exponentially tapered microstrip balun (ETMB) is one of the most efficient baluns used to feed spiral antennas. According to ref. 15, the length of an ETMB should equal one-half wavelength of the lowest frequency of interest so that the ETMB can work well in its band. But the theory on the impedance conversion of a tapered line15 shows that the length of an ETMB can be made very small if the impedance at the balanced port is close to that of the unbalanced port. Consequently, a spiral antenna with low input impedance close to 50 Ω can be fed with a very short ETMB to achieve a very low profile.
1. This photograph shows the exponential-Archimedean spiral antenna (EARSA) with highly miniaturized aperture.
To demonstrate this approach, an exponential Archimedean spiral antenna (EARSA) with highly miniaturized aperture and extremely low profile will be detailed in this report. The antenna is constructed in two parts: a sinuous meander Archimedean spiral line used to miniaturize the aperture and a controlled-width exponential spiral line that helps minimize the input impedance. Theoretically, when the ratio of the EARSA’s input impedance to 50 Ω is equal to unity, the length of the ETMB can be arbitrarily small and its impedance conversion characteristic unchanged, making possible an EARSA with truly low profile.
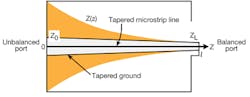
By transmission-line theory,15 a quarter-wavelength transformer offers a simple means of matching any real load impedance to any line impedance. A quarter-wave transformer provides a simple means of matching any real load impedance to any line impedance. For applications requiring more bandwidth than a single quarter-wave section can provide, multisection matching transformers can be connected serially. As the number of discrete sections increases, the step changes in characteristic impedances between the sections become smaller. A larger number of transformer sections begins to approach the structure of a continuously tapered line, such as the exponentially tapered line shown in Fig. 2.
2. A tapered microstrip transmission line is the essential component of the impedance convertor.
According to the theory on the impedance conversion of an exponentially tapered line, the convertor can work well at the smallest length, given that:
ZL/Z0 and reflection coefficient magnitude |ΓL|. The smallest length, lmin, is found from the relationship:
If the ETMB is designed on a substrate with relative permittivity of εr, then an empirical formula for calculating lmin can be found after substituting 2πεrλ0 for β, as shown in Eq. 2:
where:
λ0 = the free-space wavelength of the lowest operating frequency of the antenna, and
β = the propagation constant of the substrate material.
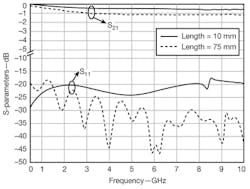
Equation 2 indicates that an ETMB will work well for a wideband impedance conversion for any length and ratio combination of ZL/Z0 that equals 1. To evaluate the effectiveness of an ETMB, one was modeled on a 1-mm-thick circuit substrate with relative permittivity of 4.3 and loss tangent of 0.003. When an ETMB with microstrip line that is not tapered is simulated as part of a back-to-back structure, it is clear that shorter ETMBs result in less transmission loss, with respectable reflection coefficient. Figure 3 shows simulated S-parameters for back-to-back ETMB structures with lengths of 10 and 75 mm, or almost one-half the wavelength at 1 GHz.
3. These simulations show S-parameters for the 10- and 75-mm ETMBs.
4. This diagram shows the layout of the spiral line essentially to the antenna.
From ref. 16, it is known that “infinite balun” is one of the most effective ways to feed Equiangular spiral antennas. One prominent characteristic of infinite balun is its remarkable impedance conversion in ultrawideband, which is used in this paper to decrease the input impedance of ARSA and achieve a low value of ZL/Z0 for the ETMB. The EARSA antenna arm consists of two parts: an exponential spiral line and a sinuous meander Archimedean spiral line, both the lines are of the same width, as shown in Fig. 4. The exponential spiral line is defined by Eq. 3:
where:
r0 = the original radius;
a1 = the spiral constant; and
φ = the winding angle.
The sinuous meander Archimedean spiral line is given by Eq. 4:
where:
r1 = the final radius of the exponential spiral line;
a2 = the spiral constant;
m = the amplitude of the sine wave;
n = angular frequency of the sine wave; and
φ1 = the final winding of the exponential spiral line.
In terms of computer modeling, the final winding angle of the Archimedean spiral line is
φ2.
To achieve a ZL/Z0 value that is close to the ideal 1, the parameters above should be carefully tuned. The structural parameters of the antenna have been collected in the table. The antenna arm is 1 mm wide and the final radius of the antenna is 41.5 mm.
5. These plots show the input impedances for a typical ARSA and for the proposed antenna, from DC to 10 GHz.
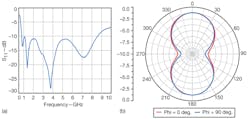
Figure 5 shows plots of input impedance for the EARSA and for a typical ARSA with the same initial radius, Archimedean spiral constant, and final radius, demonstrating the low impedance characteristic of the proposed structure. The input impedance and the characteristic impedance at the balanced port of the ETMB can be set to 50 Ω. As indicated by Fig. 2, it is reasonable to feed the antenna with a 10-mm-long ETMB; the plot of S11 for the integrated model in Fig. 6(a) shows that S11s below -10 dB from 0.8 to 8.6 GHz.
6. These simulations show the results for the integrated model of the antenna and balun (a) and the reflection coefficient (b) radiation pattern at 0.8 GHz in two orthogonal planes.
The large reflection at frequencies to 8.6 GHz should be linked to the large inductance that is almost the same to the real part of the impedance, as shown in Fig. 5. The radiation pattern at 0.8 GHz shown in Fig. 6(b) demonstrates that the balun has excellent characteristic of unbalanced-balanced mode transformation, even if it is only 0.027 times as long as the wavelength at 0.8 GHz.
Figure 7(a) shows a photograph of the back-to-back ETMB for the performance evaluation. The measured S-parameters in Fig. 7(b) indicate that S21 is greater than -2 dB from 0.5 to 10 GHz. Considering the loss of the SMA connector and the double length of the balun, the ETMB should perform well in any impedance conversions and unbalanced-balanced mode transformations between 0.5 and 10 GHz.
7. The photograph (a) shows the tapered ground and microstrip line while the plots (b) show the S-parameters.
The EARSA was etched on a 1-mm-thick substrate with permittivity of 4.3. To achieve unidirectional radiation, a 10-mm-deep cavity filled with absorber material reinforces the back of the antenna (Fig. 1). The radius of the packaged antenna is 50 mm, while the height is 10 mm.
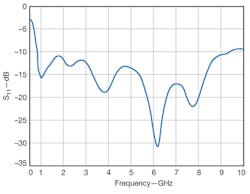
8. This plot shows the measured reflection coefficient (S11}) for the antenna through 10 GHz.
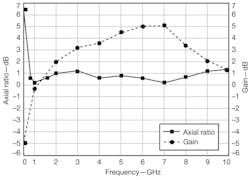
The antenna’s reflection coefficient was measured with a commercial microwave vector network analyzer (VNA). The results shown in Fig. 8 indicate good performance between 0.8 and 9.4 GHz. The lowest measured operating frequency compares to the simulated results, with the measured reflection coefficient at the highest operating frequencies in excess of the simulation result due to the effects of the absorber material. Figure 9 shows the gain and broadside axial ratio as measured at discrete frequencies in an anechoic chamber. Figure 10 shows the radiation patterns in mutually perpendicular planes at several frequencies. The measured results indicate that the EARSA works well from 0.8 to 9.4 GHz, with reflection coefficient of less than -10 dB and broadside axial ratio of less than 3 dB. Compared with a typical ARSA working at the same lowest frequency, the EARSA offers a 78.62% reduction in area. It boasts a profile that is only 10 mm deep, or only about 0.027 times the physical wavelength at 0.8 GHz.
9. These curves represent the measured broadside axial ratio and gain for the spiral antenna.
10. These radiation patterns were measured at (a) 0.8 GHz, (b) 3 GHz, (c) 6 GHz, and (d) 8 GHz.
In summary, a new type of ARSA, the EARSA, was designed with low input impedance and a shallow cavity. The input impedance of a standard ARSA can be decreased by adding a controlled-width exponentially spiral line which is characterized by impedance conversion. Simulated and measured results show that this structure significantly reduces the input impedance of the ARSA. As a result, an EARSA developed with a short, 10-mm-long ETMB was fully capable of handling the impedance conversion and unbalanced-balanced mode transformation required. The miniaturized EARSA works well from 0.8 to 9.4 GHz, with a profile only 0.027 times as long as the free-space wavelength of a 0.8-GHz signal. The antenna features a 78.62% reduction in area compared to a standard ARSA with the same low-end frequency, achieved by meandering the Archimedean spiral lines.
Wang Yawei, Doctor
Wang Guangming, Professor
Liang Jiangang, Associate Professor
Microwave Lab, No. 25 Mailbox, Sanyuan Shaanxi Province, 713800, People’s Republic of China, e-mail (Wang Yawei): [email protected]
References
1. H. Nakano, “A Meander Spiral Antenna,” IEEE Antennas and Propagation Society (AP-S) International Symposium Digest, 2004, pp. 2243-2246.
2. B.A. Kramer, C.-C. Chen, and J.L. Volakis, “Size Reduction of a Low-Profile Spiral Antenna Using Inductive and Dielectric Loading,” IEEE Antennas and Wireless Propagation Letters, Vol. 7, 2008, pp. 22-25.
3. Zhu Yu-xiao, Zhong Shun-shi, and Xu Sai-qing, “Miniaturized Compound Spiral Slot Antenna,” Microwave and Optical Technology Letters, Vol. 50, No. 11, 2008, pp. 2799-2801.
4. M.W. Numberger and J.L. Volakis, “New Termination for Ultra-Wideband Slot Spirals,” IEEE Transactions on Antennas and Propagation, Vol. 50, No. 1, 2002, pp. 82-85.
5. Ya-Wei Wang, Guang-Ming Wang, and Hui-Yong Zeng, “Design of a New Meander Archimedean Spiral Antenna,” Microwave and Optical Technology Letters, Vol. 52, No. 10, 2010, pp. 2384-2387.
6. H. Nakano, S. Sasaki, H. Oyanagi, et al., “Cavity-backed Archimedean Spiral Antenna with Strip Absorber,” IET Microwaves Antennas & Propagation, Vol. 2, No. 7, 2008, pp. 725-730.
7. H. Nakano, K. Kikkawa, Y. Iitsuka, et al., “Equiangular Spiral Antenna Backed by a Shallow Cavity with Absorbing Strips,” IEEE Transactions on Antennas and Propagation, Vol. 56, No. 8, 2008, pp. 2742-2747.
8. Hisamatsu Nakano, Tatsuya Igarashi, Hiroshi Oyanagi, et al., “Unbalanced-Mode Spiral Antenna Backed by an Extremely Shallow Cavity,” IEEE Transactions on Antennas and Propagation, Vol. 57, No. 6, 2009, pp. 1625-1633.
9. Brad A. Kramer, Stavros Koulouridis, Chi-Chih Chen, et al., “A Novel Reflective Surface for an UHF Spiral Antenna,” IEEE Antennas and Wireless Propagation Letters, Vol. 5, 2006, pp. 32-24.
10. Hisamatsu Nakano, Kazuo Hitosugi, Naoki Tatsuzawa, et al., “Effects on the Radiation Characteristics of Using a Corrugated Reflector with a Helical Antenna and an Electromagnetic Band-Gap Reflector with a Spiral Antenna,” IEEE Transactions on Antennas and Propagation, Vol. 53, No. 1, 2005, pp. 191-199.
11. L. Schreider, X. Begaud, M. Soiron, et al., “Broadband Archimedean Spiral Antenna Above a Loaded Electromagnetic Band Gap Substrate,” IET Microwaves & Antenna Propagation, Vol. 1, No. 1 2007, pp. 212-216.
12. Hisamatsu Nakano, Katsuki Kikkawa, Morihiro Kondo, et al., “Low-Profile Equiangular Spiral Antenna Backed by an EBG Reflector,” IEEE Transactions on Antennas and Propagation, Vol. 57, No. 5, 2009, pp. 1309-1318.
13. Hisamatsu Nakano, Ryohei Satake, and Junji Yamauchi, “Extremely Low-Profile Single-Arm Wideband Spiral Antenna Radiating a Circularly Polarized Wave,” IEEE Transactions on Antennas and Propagation, Vol. 58, No. 5, 2010, pp. 1511-1520.
14. Chunheng Liu, Yueguang Lu, Chunlei Du, et al., “The Broadband Spiral Antenna Design Based on Hybrid Backed-Cavity,” IEEE Transactions on Antennas and Propagation, Vol. 58, No. 6, 2010, pp. 1876-1882.
15. David M. Pozar, Microwave Engineering, 3rd ed., Wiley, New York, 2006, p. 257.
16. John D. Dyson, “The Equiangular Spiral Antenna,” IRE Transactions on Antennas and Propagation, Vol. 7, No. 2, 1959, pp. 181-187.
This file type includes high resolution graphics and schematics when applicable.