Metamaterials Form Miniature Bandstop Filters
This file type includes high resolution graphics and schematics.
Metamaterials, which exhibit simultaneous negative permittivity and permeability, offer many intriguing possibilities for high-frequency circuits such as filters. Through the use of such left-handed materials (LHMs) as they are known and subwavelength split-ring resonators (SRRs) and complementary split ring resonators (CSRRs), it may be possible to build compact microstrip bandstop filters for use at microwave frequencies. The use of SRRs and CSRRs for miniature microwave filters will be investigated in this article, with the aid of analysis performed by means of finite-element-method (FEM) software.
The usefulness of metamaterials have been reported often, with the electromagnetic (EM) properties of these materials first predicted by Veselago.1 The properties of these materials are based on negative values of the dielectric constant, ε, and the permittivity, μ, with LHMs exhibiting negative refractive indices resulting in antiparallel phase and group velocities.2,3 For a LHM, the wave vector forms a left-handed triplet with vectors and wave fronts, with propagating EM waves traveling towards the source—i.e., opposite the direction of energy flow through the medium.
The first artificial LHM operating in the microwave region was reported by Smith, et al.4 Pendry, et al.5 proposed to combine a periodic array of metallic posts with a periodic structure consisting of SRRs. The SRR is one of the essential structures of metamaterials. It produces a negative effective μ near the resonant frequency while the metallic wires of a SRR behave like a two-dimensional plasma, with negative ε to the plasma frequency. Left-handed wave propagation has also been demonstrated in one-dimensional configurations consisting of a metallic rectangular waveguide operating below cutoff and periodically loaded with SRRs.6
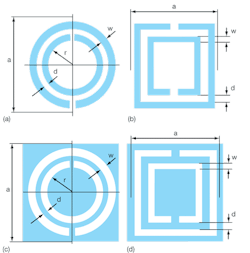
1. These layouts show (a) circular and (b) square split-ring resonators, and (c) circular and (d) square complementary split-ring resonators.
Previous structures that had exhibited left-handed propagation effects were not considered as potential component candidates in microwave and wireless systems, where compatibility with planar circuit technology is desirable. LHMs based on planar transmission lines have been reported by Grbic, et al.,7 demonstrating the existence of backward-wave radiation in a host coplanar waveguide loaded with series capacitors and shunt connected inductors. With the aid of the EM duality theorem, it follows that negative μ can be obtained from a complementary SRR etched in the ground plane of a microstrip line.
The present authors have taken advantage of the small electrical sizes of SRRs at their resonant frequencies (typically one-tenth or less the value of the free space wavelength) to design planar compact microstrip bandstop and ultrawideband (UWB) filters using two techniques. One of these involves microstrip line loaded with SRRs, while the other uses a microstrip circuit with CSRRs etched in the ground plane of the printed-circuit board (PCB), beneath the microstrip line. The authors have designed metamaterial CSRR filters, with the CSRRs integrated into the active regions of the filters.
As Fig. 1 shows, a CSRR is the dual counterpart of an SRR, which is a constitutive element for the synthesis of negative permittivity media. CSRRs are mainly driven by an axial time-varying electric field, rather than an axial magnetic field (as in the case of SRRs). The rationale behind using metamaterial CSRRs was to promote the miniaturization of bandstop and UWB filters as viable alternatives to existing designs,2-6 without compromises in performance or size.
The frequency selectivity of CSRRs suggests their suitability for use in filters, since they are ideal for fabrication in planar constructions when they are mainly excited by an axial time-varying electric field.11 CSRRs are formed by parallel combinations of inductors (Ls) and capacitors (Cs), with the LC resonant tank electromagnetically coupled to the host line. The equivalent-circuit model for CSRRs, loaded transmission line, and its relevant values of the inductors and capacitors can be calculated using methods described in ref. 8.
2. This plot shows the frequency response of an SRR-based coplanar-waveguide (CPW) left-handed line from 1 to 10 GHz.
Figures 1(c) and 1(d) present the conventional layout of a CSRR microstrip structure where the CSRRs are etched into the ground plane beneath the microstrip. The possibility of obtaining such broad frequency response by means of balanced lines opens the door to the application of these structures in the design of broadband filters. In addition, the position of the transmission zeroes can be adjusted to eliminate spurious bands and to control out-of-band rejection, which can also be improved by increasing the number of resonator/filter stages. These properties have been exploited and applied to the design of several kinds of filters.
In exploring the possibilities of filters based on CSRRs, the first step involved combining different cells with right-handed and left-handed behaviors to obtain bandpass response.9,10 These two kinds of lines present a transmission zero above and below the first transmission band, making it possible to achieve high-frequency bandpass filter behavior with sharp cutoffs on both sides of the passband (Figs. 2-4). Poor rejection was the consequence of only using one kind of cell.
3. This plot shows the frequency response of an SRR-based CPW) right-handed line from 1 to 10 GHz.
Alternate right/left-handed cells with circular CSRRs were fabricated using a number of different commercial circuit-board materials, including RO3010™ high-frequency laminates from Rogers Corp. The RO3010 circuit material is a ceramic-filled polytetrafluoroethylene (PTFE) composite with a relative dielectric constant, εr, of 10.2 at 10 GHz in the z axis (thickness) of the material. It has a coefficient of thermal expansion (CTE) of 17 pp/°C which is comparable to that of copper for good mechanical stability over a wide temperature range. For fabricating the CSRRs, a substrate with thickness, h, of 0.49 mm was used. The radius of the smaller SRRs was r = 1.39 mm, with the width and distance between the rings, d, equal to 0.2 mm and the same in all of the SRRs. The radius of the bigger SRRs was r = 1.52 mm. The wire width, ww, was 2.16 mm, while the gap length, lg was 1.6 mm and the total length of the filter was 1.5 cm.
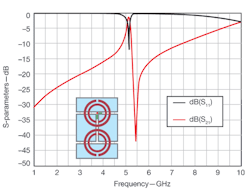
4. This plot shows the frequency response of the filter combining one right-handed and two left-handed unit cells (the metallic parts are depicted in black for the top layer and in grey for the bottom layer of the substrate).
This file type includes high resolution graphics and schematics.
A second type of filters that was designed and analyzed were based on alternate right-/left-handed cells with square CSRRs. With the help of HFSS three-dimensional (3D) EM simulation software from Ansys, a CSRR filter was designed based on the RO3010 circuit material. The dimensions of each square consisted of external edges of 4.86 x 4.86 mm and thickness, h, of 0.49 mm. The smaller SRR is 2.78 x 2.78 mm, with the width and distance between the rings equal to c = d = 0.2 mm and the same in all SRRs. The bigger SRRs measure 3.04 x 3.04 mm, with wire width of w = 2.16 mm, gap length, lg = 1.6 mm, and the total length of the filter at 1.5 cm.
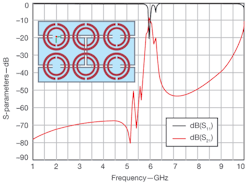
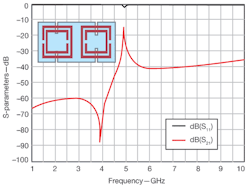
Figures 5-7 show the influence of the form of SRR on the response of the filter. SRRs and CSRRs can be used to design filters with bandwidths employing either SRR-based coplanar-waveguide (CPW) transmission lines9,12 or CSRR-based microstrip structures.10,13,14 In coplanar technology, the right-handed lines involve the combination of SRRs etched on the bottom side of the line and capacitive gaps etched on the coplanar waveguide (see Figs. 3 and 6). CSRR-based microstrip right-handed structures combine shunt inductances with CSRRs etched on the ground plane to obtain the desired response.
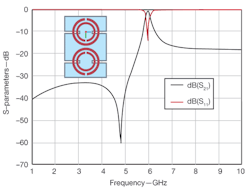
5. The S-parameters reveal the frequency response of an SRR-based CPW left-handed line.
6. The S-parameters show the frequency response of an SRR-based CPW right-handed line.
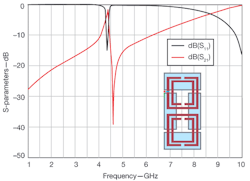
As can be seen in Figs. 4 and 7, as well as being very compact (the length of the active part is 1.5 cm), a filter with CSRRs exhibits a very selective and symmetric narrow-band response thanks to the combination of the two types of coplanar metamaterial unit cells. If compared with a conventional coupled-line filter with similar characteristics, the total length of the metamaterial filter is roughly three times shorter than the conventional filter.
To demonstrate the use of CSRRs, a standard third-order maximally flat bandpass filter with quarter-wavelength short-circuit resonators was first designed based on the formulas in ref. 15. The simulation results of the structure are shown in Fig. 8. Two CSRRs with a separation distance of 20 mm were used. The dimension of each ring is as follows: r = 1.4 mm, c = 0.25 mm, d = 0.4, and g = 0.3. The circuit board material was 0.787-mm-thick RT/duroid® 5870 laminate from Rogers Corp., which exhibits a relative dielectric constant of 2.33 at 10 GHz in the z-axis (thickness) of the material. The scattering parameters illustrate that the rings resonate at 5.60 GHz, where the insertion loss reaches more than 10 dB.
7. The S-parameters reveal the frequency response of the filter combining one right-handed and two left-handed unit cells.
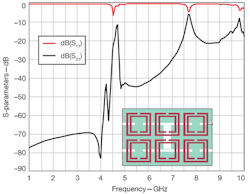
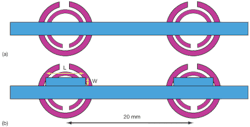
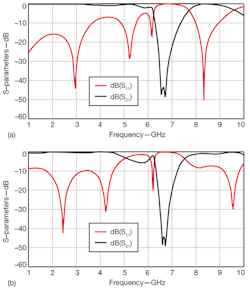
Figure 9 shows that there are problems associated with this structure. The stopband rolloff is very gradual, especially following the resonance.15 To integrate this structure into the UWB filter design, its insertion-loss and return-loss characteristics must be improved. Analysis of the structure has revealed that the poor performance is due to the impedance mismatches between the CSRRs and their host transmission line. Etching away parts of the ground plane has resulted in an increase in inductance. To compensate for this, a capacitive load in the form of an open-circuited stub with length L and width W was introduced to counter the increase in inductance [Fig. 8(b)]. The positions of the CSRRs (as they alter the field distribution) will also impact the impedance matching with the transmission line and the shape of the stopband. The improved performance in Fig. 8(b) compared to Fig. 8(a) is the result of displacing the centers of the CSRRs by 1.85 mm from the center of the microstrip.
8. The two layouts compare (a) a conventional CSRR-microstrip structure and (b) a modified CSRR-microstrip structure. The dark and gray regions represent the microstrip line and CSRRs etched in the ground plane, respectively.
Figure 9 also shows the simulation results of (a) the conventional CSRR-microstrip structure and (b) the modified CSRR-microstrip structure. The open circuited-stub has a length L of 5 mm and width W of 1.3 mm. The performance of the modified structure has been improved noticeably.The scattering parameters show that the insertion loss is below 1 dB while the return loss is better than 10 dB within the desired UWB frequency range. By slightly adjusting the position of the centers of the rings, the corresponding stop band was improved to lower and upper 3-dB points of 6.50 and 7.85 GHz, respectively.
9. These simulation results show (a) the conventional CSRR-microstrip structure and (b) the modified CSRR-microstrip structure.
This article has explored the design and analysis of compact filters based on metamaterial CSRRs. By experimenting with different combinations of CSRRs and different filter bandwidths, functions, and performance levels, filter dimensions can be reduced without the need of adding lumped elements. When size and planar structures are important, such metamaterial filters offer an attractive alternative to traditional LC filters.
References
1. V.G. Veselago, “The electrodynamics of substances with simultaneously negative values of ε and μ, ” Soviet Physics Uspekhi, Vol. 10, 1968, p. 509.
2. D.R. Smith, W.J. Padilla, D.C. Vier, S.C. Nemat-Nasser, and S. Schultz, “Composite medium with simultaneously negative permeability and permittivity,” Physical Review Letters, Vol. 84, 2000, pp. 4184-4187.
3. C. Caloz, C.-C. Chang, and T. Itoh, “A novel anisotropic uniplanar compact photonic band-gap ground plane,” to be presented in IEEE AP-S International Symposium, Boston, MA, July 2001.
4. Zeng, Wang, Zhang, and Zhu, Microwave & Optical Technology Letters, Vol. 52, No. 2, February 2010, p. 430.
5. J.B. Pendry, A.J. Holden, D.J. Robbins, and W.J. Stewart, “Magnetism from conductors and enhanced nonlinear phenomena,” IEEE Transactions on Microwave Theory & Techniques, Vol. 47, No. 11, November 1999, pp. 2075-2084.
6. R. Marqués and J. Martel, “Left-handed media Simulation and Transmission of EM Waves in Subwavelength Split-ring resonator-loaded metallic waveguides,” Physical Review Letters, paper 183901, October 2002.
7. A. Grbic and G.V. Eleftheriades, “Experimental verification of back-ward-wave radiation from a negative index metamaterial,” Journal of Applied Physics, Vol. 92, No. 10, November 2002, pp. 5930–5934.
8. M. Gil, J. Bonache, and F. Martín, “Metamaterial Filters: A Review,” Science Direct, August 2008, pp. 186-197.
9. Gil, Morata, Fernandez, Rottenberg, and De Raedt, Microelectronic Engineering, Vol. 88, 2011, pp. 1-5.
10. J. Bonache, F. Martín, F. Falcone, J. García, I. Gil, T. Lopetegi, M.A.G. Laso, R. Marqués, F. Medina, and M. Sorolla, “Super compact split ring resonators CPW band pass filters,” Proceedings of the IEEE-MTT International Microwave Symposium Digest, Fort Worth, TX, June 2004, pp. 1483–1486.
11. P. Mondal, M.K. Mandal, A. Chaktabarty, and S. Sanyal, “Compact bandpass filters with wide controllable fractional bandwidth,”IEEE Microwave & Wireless Components Letters, Vol. 16, 2006, pp. 540-542.
12. J. Bonache, F. Martín, F. Falcone, J. García-García, I. Gil, T. Lopetegi, M.A.G. Laso, R. Marqués, F. Medina, and M. Sorolla, “Compact coplanar waveguide band pass filter at S-band,” Microwave and Optical Technology Letters, Vol. 46, 2005, pp. 33-35.
13. Guo Deng and Che Li, Microwave & Optical Technology Letters, Vol. 53, No. 7, July 2011, p. 1483; Azna Velez, Duran-Sindreu, and Martin Bonache, IET Microwave Antennas & Propagation, Vol. 5, No. 3, February 2011, pp. 277-281.
14. Yang Tang, Microwave & Optical Technology Letters, Vol. 52, No. 11, November 2010, p. 2592.
15. Abid Ali and Zhirun Hu, “Metamaterial Resonator Based Wave Propagation Notch for Ultrawide band Filter applications,”IEEE Antennas & Wireless Propagation Letters, Vol. 7, 2008, pp. 210-212.
This file type includes high resolution graphics and schematics.