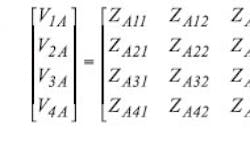Design Tunable Filters Using Feedback
Tunable microwave filters are useful in both commercial and military systems. The oldest forms of these filters are mechanical, with excellent insertion loss and power-handling capabilities, but large in size and with slow tuning speeds. For wireless systems, faster tuning speeds are required, in addition to filters with planar structures and relatively simple design procedures (as will be described in this report). Excellent tuning characteristics are possible by using capacitively loaded open ends in the coupled sections. but tunable matching sections are also needed to compensate for changes in bandwidth and insertion loss that they bring.1 These additional sections increase filter complexity, and having four varactor diodes for variable capacitance can add to the insertion loss. Moreover, the periodicity of the structure depends heavily on the accurate tuning of each varactor. To achieve an improved design, the number of varactor diodes must be reduced without sacrificing tenability.
A filter design based on a tunable element in series with the filter sections yielded very low tunability. The matching section design for the capacitor was difficult. As a result, there was increased reflection, affecting the tunability. Although the design was simple, it suffered from many drawbacks.2 To improve tenability while keeping the design simple, a tunable filter using feedback loop was designed, analyzed, and simulated by computer-aided-engineering (CAE) software, including the Advanced Design System (ADS) from Agilent Technologies and MATLAB from The Math Works.
There was a possibility of electronically tuning this filter using varactor diodes if they were connected in the feedback. To begin with, a third-order filter was designed. Upon addition of the capacitive feedback sections from one open ended port of a coupled section to an open ended port of the previous coupled section, as shown in Fig.1, the center frequency shifted. Because of the geometry, it was not possible to use only capacitors for feedback. The design required insertion of microstrip transmission lines connected from one end of the coupler to the capacitor and vice versa (Fig. 2).
A plot of filter bandwidth versus feedback section width was obtained using ADS. The width of the strips was determined for a bandwidth of 20 MHz. From Fig. 3, it can be seen that the microstrip linewidth is 4.742 mm for a bandwidth of 20 MHz with a feedback capacitor value of 3 pF. The characteristic impedance of the microstrip line corresponding to this width is 50 Ω. The length of the feedback sections was determined by taking the geometry of the network into account.
Analysis of a filter with a feedback network connected between consecutive cascaded coupled sections is not straightforward since the logic of multiplying ABCD matrices for each coupled line moving in the forward direction no longer holds true. This is because the input and output of each coupled lines are dependent on the previous or following coupled section depending on the section under consideration.3 This leads to the analysis of a coupled line network with the ABCD matrix of the feedback section embedded into it.4
This analysis begins with only two coupled sections, A and B, connected with a feedback network (Fig. 4). The output of the first coupled section A at port 3 is connected to the input of the next coupled section B. Energy is fed back from coupled section B at port 4 to coupled section A at port 2 via a capacitive feedback loop. The impedance matrix of the coupled section A is as follows (Eq. 1):
This impedance matrix is a function of even- and odd-mode voltages, α and . But now port 2 plays no part in the analysis because it has an open-circuited end and in no way affects the other voltages and currents once the input-output relationship of the coupled section gets set. Hence, the second row throughout and the second column of the impedance matrix are deleted. This leads to Eq. 2:
The matrices are now broken into blocks to solve the equations in order to get them rearranged into a form to put V4A and I4A on the right-hand side of Eq. 2. This will simplify the analysis in the next round, since V4A and I4A are related to V2B and I2B by an ABCD matrix of the feedback element Eq. 3:
Similar analysis can be made for coupled line B. After switching columns and solving matrix blocks, the matrix relations can be written in the form of Eq. 4:
Continue on Page 2
Page Title
It can then be written that V4A and I4A are related to V2B and I2B by a transmission matrix of the feedback element:
Using Eq. 3, we express the input-output relationship can be expressed in terms of V4B and I4B by incorporating the ABCD matrix. This leads to Eq. 6:
Where:
The next simplification that can made owes to the fact that:
Substituting these conditions into Eqs. 6 and 4, it is now possible to write the equations for V3A and I3A for section A and V1B and I1B for section B:
Addressing Eqs. 9 and 10 results in Eq. 11:
This leads to an equation of the form:
Now that it is possible to express V4B and I4B in terns of I1A and I3B, it is also possible to substitute in the equations for V1A and V3B from Eqs. 6 and 4, respectively:
Substituting for V4B and I4B from Eq. 12 into Eqs. 13 and 14 provides an impedance matrix for the two coupled sections connected in feedback, with the form represented by the equality in Eq. 15:
where Eq. 16 represents the Z-matrix in a 2 2 format:
Hence, the analysis of the two coupled sections connected by a tunable feedback section condenses to a two-port network analysis. This Z-matrix can be converted to an equivalent ABCD matrix ABCD'fb. In this present case of a third-order filter with four sections, the next two coupled sections are also connected to each other using feedback. This block will have a similar ABCD matrix as we look from port 2. The ABCD matrix of this section ABCD'fb is given as:
Where:
Continue on Page 3
Page Title
This ABCD matrix is multiplied to the ABCD matrix of the other block. By then multiplying the ABCD matrices of the matching sections, the overall ABCD matrix representing the tunable bandpass filter is computed. The S-parameters of the bandpass filter are then found by converting the overall ABCD to its S-matrix equivalent.
This procedure of obtaining the S-matrix was coded in MATLAB. The results were then compared with a similar ADS schematic (Fig. 5 and Fig. 6). The bandwidth obtained in the MATLAB simulation was smaller compared to the ADS simulation results.
For a 3-pF feedback capacitor, the center frequency obtained through MATLAB was 1.516 GHz while the ADS results showed it to be 1.556 GHz. For a 5-pF feedback capacitor, the center frequency obtained through MATLAB was 1.468 GHz while ADS showed it to be 1.479 GHz. The experimental-circuit-board bandwidth is larger than the ADS simulated bandwidth, as the feedback capacitance is changed from 3 to 5 pF. This increase in bandwidth in the circuit-board design is because of the fringing capacitances caused by open-ended effects.5
The observed return loss and insertion loss are shown in Fig. 7 and Fig. 8, respectively. The center frequency of the simulated response drops from 1.556 to 1.479 GHz when the feedback capacitance was changed from 3 pF to 5 pF.
The ADS simulated bandwidth varies from 20 MHz to 19.97 MHz as the feedback capacitance is changed from 3 pF to 5 pF. The schematic shows a minimum S11 of -7.734 dB and maximum S21 of -5.687 dB for feedback capacitance of 5 pF. For a 3-pF capacitance, ADS results showed a minimum S21 of -8.18 dB and maximum S21 of -5.848 dB. The combined responses are showed in Fig. 9.
The tuning of the filter is from 1.474 to 1.573 GHz, an overall range of 99 MHz. The feedback capacitance range is varied from 2.7 to 5.2 pF. Figure 10 shows ADS computer-aided-engineering (CAE) simulations of the return and insertion losses over the tuning range. In both cases, the loss curves are remarkably consistent with frequency, over the simulation range from 1.30 to 1.70 GHz. In both cases, the value of the feedback capacitor was changed in 0.5-pF steps from 2.7 to 5.2 pF. While the simulated return loss (left) showed slight drops in value at the lower and upper ranges of the tuning capacitance values, the simulated insertion loss showed a slight increase as might be expected at the higher frequencies (higher capacitance values). Figure 11 displays the simulated variation of bandwidth and center frequency as the capacitance is tuned. The bandwidth varies around a median value of about 20 MHz as the values of the tuning capacitance are changed from 2.7 to 5.2 pF (left) while the center frequency drops as might be expected (right) as the tuning capacitance is increased to a maximum value of 5.2 pF.
This tuning range can be increased by increasing the width of the feedback microstrip lines.6 But in the process of increasing the tuning range would also impact the response of the filter. Reducing the width of the feedback microstrip lines actually improves the return loss as shown in Fig. 12 since it is being matched to the high input impedance as seen from the feedback section, and this cleaner impedance transition results in less reflections and improved return-loss performance. But it would also imply that the filtering action is being bypassed.7 This affects the tuning performance since lower amount of energy passes through the feedback sections, as shown in Fig. 13. Figure 14 displays the variation of center frequency as the feedback microstrip line width is tuned.
Group delay is a measure of the time taken by a signal to travel from the input port to the output port. From Fig. 15, it can be seen that the group delay remains near constant as the feedback capacitor is varied from 2.7 to 5.2 pF.
In summary, the use of feedback in this design provided effective tuning while still maintaining design flexibility compared to other tunable-filter design approaches. The design was simple and easy to fabricate. By performing mathematical analysis and writing corresponding MATLAB code (effects due to conductor and dielectric losses were ignored in the analysis), as well as applying ADS, a final design was developed.
The final design involved using tuning elements attached to an open end of each coupled section. This required tunable matching sections to compensate for the reflection across the tuning range from any impedance mismatches across the broad frequency range. The design involved using a tunable capacitor in series with the coupled sections and had high insertion loss of about 20 dB. Unfortunately, a spurious mode due to the inhomogeneity of the microstrip transmission line affects the filter performance, but the design can be modified to diminish these spurious effects. Work continues on the filter design method, with other efforts involving an amplifier in feedback with the filter. Mathematically, the center frequency should shift as the gain of the amplifier is varied since the poles of the transfer function change. Such an approach could be applied to the design of a multiband filter.
REFERENCES
1. B. Carey-Smith, P. Warr, M. Beach, and T. Nesimoglu, "Transmission-line filters with capacitively loaded coupled lines," IEEE Transactions on Microwave Theory and Techniques, Vol. 53, 2005, pp. 777-785.
2. J.C. Estes, "Tunable RF bandpass pass filter with variable resonator coupling," IEEE MTT-S International Microwave Symposium Digest, 2008.
3. B.-W. Kim and S.-W. Yun, "Varactor-tuned combline bandpass filter using step-impedance microstrip lines," IEEE Transactions on Microwave Theory and Techniques, Vol. 52, No. 4, 2004, pp. 1279-1283.
4. B. Kapilevich, "A varactor-tunable filter with constant bandwidth and loss compensation," Microwave Journal, Vol. 50, No. 6, June 2007, pp. 106-114.
5. I. Shapir, V.A. Sharir, and D.G. Swanson, "TEM modeling of parasitic bandwidth expansion in combline filters," IEEE Transactions on Microwave Theory and Techniques, Vol. 47, 1999, pp. 1664-1669.
6. J. Lee and K. Sarabandi, "An analytic design method for microstrip tunable filters," IEEE Transactions on Microwave Theory and Techniques, Vol. 56, No. 7, July 2008, pp. 1699-1706.
7. J. Nath, D. Ghosh, J.-P. Maria, A. I. Kingon, W. Fathelbab, P. D. Franzon, and M. B. Steer, "An electronically tunable microstrip bandpass filter using thin-film Barium-Strontium-Titanate (BST) varactors," IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 9, September 2005, pp. 2707-2711.