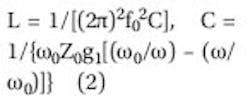DGS Lowpass Filters Extend Wide Stopbands
Jian-Kang Xiao, Yu-Feng Zhu, and Jeffrey S. Fu
LOWPASS FILTERS (LPFs) can channel desired signals while rejecting the highest-frequency signal components. But fabricating LPFs with wide stopbands in miniature packages is challenging. Fortunately, microstrip transmission lines and nonuniform defected ground structures (DGS) can be combined to form small, practical LPFs with wide stopbands.
This study will provide a summary of DGS design techniques in microstrip and how to realize wide-stopband LPFs using periodical and fractal DGS. Measurements will show that an LPF formed with nonuniform dumbbell-shaped DGS units etched under a stepped-impedance microstrip line provides enhanced performance of transmission zeros and return loss compared to a filter fabricated with uniform DGS cells and uniform microstrip line; it is also smaller in size. Through the use of fractal DGS units, the filter's out-of-band suppression can also be enhanced.
LPFs play key roles in RF/microwave systems, for rejection of higher-frequency harmonic signals and spurious responses.1,2 Conventional implementation of an LPF involves open stubs or stepped-impedance microstrip lines. Such structures, however, yield responses that are limited in terms of cutoffonly by increasing the number of sections can rejection be increased, an approach which also increases passband loss and filter size.
Some newer methods, such as the complementary split ring resonator (CSRR) technique3 and the DGS4-6 approach, developed from photonic bandgap (PBG) methods, have been applied to improve LPF design. The DGS method has proven effective for high harmonic suppression with stopband performance extending well into the microwave rangeespecially periodical DGSs, which extend the stopband significantly. Periodical dumbbell DGSs support a wider stopband since the electromagnetic (EM) field is highly concentrated under the microstrip line (ML).
A DGS is formed by etching a defected pattern on the metallic ground plane of a printed-circuit-board (PCB) substrate. This structure increases the effective capacitance and inductance of a microstrip line, controlling spurious responses by rejecting harmonics in microwave circuits. The use of DGSs can improve the performance of filters and other microwave components. In some cases, DGSs have yielded wider stopbands for suppressing spurious, surface-wave propagation, and leakage transmissions.5,6
However, the stopband width is related to the number of DGS cells, with wider stopbands implying larger circuit sizes. Normally, dumbbell-shaped DGS cells provide deeper band rejection and a better rejection bandwidth than circularshaped DGS cells.7 But LPFs based on uniform dumbbell-shaped DGSs exhibit undesired peaks which degrade the rejection bandwidth expansion.8 For that reason, experiments were performed on LPFs based on nonuniform DGSs to better understand their potential for highfrequency applications.
The word "fractal" means broken or fractured, and designates figures and structures without characteristic length. Basic fractal geometries include Koch fractal, Minkowski fractal, Sierpinski fractal, and Hilbert fractal geometries. Something with a fractal nature has self-similarity and is space filling. Classical fractal geometries generated by mathematical methods always have strict self-similarity, and can be called well-regulated fractals; the most applied configurations are irregular fractals with rough self-similarity.
Two types of fractals are applied for microwave filter design: line or patch-based and ground-based fractals. Fractals can change a filter's current pattern, so that current is distributed along the flexural conductor surface instead of the original surface. In effect, the electric length is increased and the performance is modified.
Chebyshev dumbbell-DGS-assisted lowpass filters were developed to demonstrate the effective use of fractals on microwave design. The ground plane of a standard 50- Ω transmission line and a stepped-impedance transmission line were perturbed by nonuniform dumbbell DGSs and Minkowski fractal DGSs to generate an ultrawide rejection band for higher-order harmonic suppression. By using the DGS techniques, new lowpass filters with transmission zeros and ultrawide stopband were implemented, and the design verified by experiment.
Compared with a traditional dumbbell DGS, the new DGS unit shown in Fig. 1 has a higher slow-wave factor which makes it possible to achieve a more compact circuit, steeper band rejection, and more exterior quality-factor (Q) value. Periodical DGS elements (Fig. 2) can be classified as horizontal periodical DGS (HPDGS) and vertical periodical DGS (VPDGS); a dumbbellshaped DGS is shown in Fig. 2(a).
A dumbbell-shaped DGS can be replaced by a parallel LC circuit,7 where inductance L denotes the operation of the rectangular lattice in the defected unit, and capacitance C denotes the operation of the slit between the two rectangular lattices Fig. 3(a)>. Inductance L increases as the area of the rectangular lattice increases, while C decreases as the width of slit increases. The frequency response of the dumbbell-shaped DGS unit is equivalent to that of the first Butterworth lowpass filter prototype shown in Fig. 3(b), so that the equivalent-circuit elements of the dumbbell-shaped unit can be expressed7 as Eqs. 1 and 2:
jXLC = j/{Ω0c0/Ω) (Ω/Ω0)>} (1)
and
where
f0 = the operating frequency and Ω0 = 2πf0.
Page Title
The DGS unit can largely be analyzed by the frequency characteristics of the first Butterworth lowpass filter prototype; however, this kind of equivalent circuit is an ideal model with no loss. A more precise equivalent circuit is the p-type model9 because of its microstrip line and dielectric losses, and because the effects of electromagnetic (EM) radiation are fully considered. The p-type circuit simulates the amplitude-frequency and phase-frequency characteristics of a DGS simultaneously, as Fig. 3(c) shows. If the impedances of the three LC parallel units are transformed into admittances, the DGS equivalent circuit can be simplified into a typical p-type two-port network,9 as is shown in Fig. 3(d), and the ABCD matrix can be expressed as Eq. 3:
If the two-DGS-patterned center spacing of a periodical DGS is defined as "a," as Fig. 2(b) shows, Bragg's condition is satisfied, and it can be expressed as Eq. 4:
where
= the wave number in the dielectric slab,
f0 = the center frequency in the stopband,
ee = the effective relative dielectric permittivity of the dielectric slab, and
c = the speed of light in free space.
The dumbbell DGS design can also be expressed by using antenna similarities. With the rapid development of modern communication systems, more miniature microwave filters with wide stopbands are required. Periodical dumbbell DGSs extend the stopband significantly since the EM field is highly concentrated under the microstrip line. Here, new lowpass filters with periodical dumbbell DGSs are designed on Duroid substrate with a relative dielectric constant of 2.2 and thickness of H = 0.8 mm.
In the research, the performance of LPF with periodical uniform DGSs was observed to have a much wider stopband compared with a nonperiodical DGS or the new DGS. However, the insertion-loss and return-loss performance were inadequate and the size of the circuit was large. As a result, a LPF with periodical nonuniform DGSs was designed in an attempt to improve the performance (Fig. 4). Stepped-impedance microstrip line Fig. 5(a)> was also used for the improvement; its equivalent circuit is shown in Fig. 5(b), with the equivalent capacitance, Cs , expressed10 by Eq. 5:
and the equivalent inductance Li (i = 1, 2) shown by Eq. 6:
where Lw1 and Lw2 = the inductance of the unit microstrip line corresponding to the widths, w1 and w2, respectively; Lwi = Z0i(ee)0.5/c; and Z0i = the characteristic impedance of the microstrip line corresponding to the widths, w1 and w2. For w1 = 2.46 mm and w2 = 4.92 mm, the corresponding microstrip line can be calculated as having impedances Z01 = 50 Ω and Z01 = 30.3 Ω, respectively, and L can be expressed as Eq. 7:
where H = the thickness of dielectric substrate.
The simulated S-parameters of the dumbbell DGS circuit and filter frequency responses are shown in Fig. 6 and Fig. 7, respectively, and the performance of the periodical nonuniform DGS is described in the table. As can be seen, the cutoff frequency increases with decreasing DGS dimension. With a stepped impedance line, the LPF has better out-of-band rejection, improved return loss (no less than 13 dB), and better harmonic suppression compared with the LPF with uniform 50-Ω microstrip line. The LPF with periodical nonuniform DGSs has a wider stopband performance compared with a LPF with periodical uniform DGSs because different DGS has different cutoff frequency as Fig. 6 shows; thus, the bandwidth of stopband is greatly extended.
To reduce filter size, an improved LPF is proposed Figs. 8(a) and (b)>. The new LPF has four nonuniform DGSs which yield a size reduction of about 50 percent compared with the LPF using eight nonuniform DGSs shown in Fig. 4. The simulated frequency responses of the LPF with four nonuniform DGSs are shown in Fig. 8(c). The LPF with a stepped-impedance microstrip line has a cutoff frequency of 3.36 GHz and a transmission zero with attenuation of 63 dB. This filter has a return loss of no less than15 dB, and a steeper out-of-band suppression, and simultaneously, a wider stopband width of more than 10 GHz. For this LPF, all performance parameters exceed those of the LPF with 50-O uniform microstrip line Fig. 8(a)>.
To verify the design, the lowpass filter with four nonuniform DGSs was fabricated and tested (Fig. 9). Measurements were performed with a model E5071C vector network analyzer (VNA) from Agilent Technologies. Those results show that the filter has transmission zeros and ultrawideband stopband within 3.4 to 15.0 GHz, a frequency span more than three times the cutoff frequency of the filter. The measured results match closely with early simulations.
Lowpass filters with nonuniform fractal DGS units and cell reductions were also designed, using the same filter substrate and height as the earlier filters. Figure 10 shows the Minkowski fractal structures and the proposed Minkowski fractal DGS. Figure 11 shows a Minkowski fractal DGS lowpass filter using stepped-impedance microstrip line and four nonuniform DGSs. Figure 12 shows simulated responses, with and without fractals, using a 50-Ω microstrip line. The response with the fractal shows better selectivity and out-of-band suppression by the two transmission zeros at 4.09 and 5.45 GHz, with attenuation of 33.4 and 62.3 dB, respectively, and cutoff lowered to 3.26 GHz.
Figure 13 shows simulated responses of the fractal lowpass filter with uniform and stepped-impedance microstrip lines; for the stepped-impedance version, the stopband is wider and the return-loss performance is better at frequencies to below 3 GHz. The lowpass filter that was fabricated with the fractal dumbbell DGS with stepped-impedance microstrip line yielded better than 17-dB passband return loss and wide stopband of 3.2 to 15.0 GHz.
JIAN-KANG XIAO, Researcher, College of Computer and Information, Hohai University, Changzhou, 213022, China and State Key Laboratory of Millimeter Waves, Nanjing, 210096, PRC, e-mail: [email protected]
YU-FENG ZHU, Researcher, College of Computer and Information, Hohai University, Changzhou, 213022, PRC
JEFFREY S. FU, Researcher, Department of Electronic Engineering, Chang Gung University, Taoyuan, Taiwan, 333, PRC
ACKNOWLEDGMENTS This work was supported in part by Specialized Research Fund for the China Doctoral Program of Higher Education (200805611077), the Open Research Fund of China State Key Laboratory of Millimeter Waves (K201107), and the Fundamental Research Funds for China Central Universities (2010B22714).
REFERENCES
1. J. Chen, Z.-B. Weng, Y.-C. Jiao, and F.-S. Zhang, "Lowpass Filter Design of Hilbert Curve Ring Defected Ground Structure," Progress In Electromagnetics Research, Vol. PIER 70, 2007, pp. 269-280.
2. M. Yang, J. Xu, Q. Zhao, L. Peng, and G. Li, "Compact, Broad-Stopband Lowpass Filters Using Sirs-Loaded Circular Hairpin Resonators," Progress In Electromagnetics Research, Vol. PIER 102, 2010, pp. 95-106.
3. M. K. Mandal, P. Mondal, and S. Sanyal et al., "Low insertion-loss, sharp-rejection and compact microstrip low-pass filters," IEEE Microwave and Wireless Components Letters, Vol.16, No.11, 600-602, 2006.
4. C. Han-Jan, H. Tsung-Hui, and C. Chin-Sheng et al., "A novel cross-shape DGS applied to design ultra-wide stopband low-pass filters," IEEE Microwave and Wireless Components Letters, Vol. 16, No. 5, 2006, pp. 252-254.
5. D. Ahn, J-S. Park, and C-S Kim et al., "A design of the low-pass filter using novel microstrip defected ground structure," IEEE Transactions on Microwave Theory and Techniques, Vol. 49, No. 1, 2001, pp. 86-93.
6. D. Ahn, J-S. Park, C-S Kim, J. Kim, Y. Qian, and T. Itoh, "A design of the lowpass filter using novel microstrip defected ground structure," IEEE Transactions on Microwave Theory and Techniques, Vol. 49, 2001, pp. 86-93.
7. J. I. Park, C. S. Kim, J. S. Park, Y. Qian, D. Ahn, and T. Itoh, "Modeling of Photonic Bandgap and Its Application for the Lowpass Filter Design," Asia-Pacific Microwave Conference Proceedings, 1999, pp. 331334.
8. N. Mollah, F. Hossain, J.S. Fu, and D.-H. Yang, Novel technique of developing microstrip low pass filter, 2007 International Information, Communications & Signal Processing Conference, December 1-4, 2007.
9. J.-S. Park, J.-H. Kimt, J.-H. Leet et al., "A novel equivalent circuit and modeling method for defected ground structure and its application to optimization of a DGS lowpass filter," 2002 IEEE MTT-S Digest, pp. 417-420.
10. J.-M. Fu and E.-X. Feng, Advanced Electromagnetic Theory, Xian Jiaotong University Press, Xian, China, 2000.