Tiny Spiral Spans 1.4 To 10.0 GHz
Antennas for broadband and multiple-standard communications must provide excellent performance in a small area. While a spiral antenna can provide consistent radiation patterns, the size reduction is often a problem, since the antenna’s design is related to the physical wavelengths of the operating frequencies. Fortunately, a miniaturized arm-width-tapered Archimedean spiral antenna (ATARSA) has been designed that delivers outstanding performance in a size that is dramatically reduced compared to conventional spiral antennas.
The arms of the antenna are tapered to maintain self-complementarity, helping to achieve that good performance in a small size. Comparing the results of computer simulations and measurements (which agree closely), the ATARSA offers reflection coefficient and axial ratio of −10 dB and 3 dB, respectively, from 1.4 to 10.0 GHz. It features a 73.1% reduction in area compared to a typical Archimedean spiral antenna designed for the same frequency band.
Spiral antennas have long been appreciated for their stable input impedance and radiation characteristics (excellent gain, axial ratio, and radiation patterns) over several octaves. The tradeoff has been their large size when designed for low-frequency operation. As a result, a variety of techniques have been developed to reduce the size of a spiral antenna. One of the most efficient methods is to add loads to the ends of the antenna.1-10 Reactance loading can greatly decrease the phase velocity along the arms of the antenna, helping to reduce the size of the antenna by 50%.1
Resistance loading2,3 and the use of microwave absorber materials4-6 have also been used for size reductions in spiral antennas, but they weaken the current at the ends of the antenna arms—helping to achieve lower-frequency operation in a smaller antenna size, but with a sacrifice in gain performance. Tapered spiral lines have been used, as detailed in refs. 7-10, in order to improve the low-frequency response of a spiral antenna by reflecting the current from the ends of the antenna arms. As ref. 7 explains, making a tapered line thinner and with more windings on a fixed radius helps to miniaturize a spiral antenna with enhanced performance at low frequencies.
Up until now, tapered spiral lines have been applied mainly to the ends of equiangular spiral antennas rather than Archimedean spiral antennas (ARSAs)8-10 in attempts to achieve size reductions. The tapered lines have typically degraded or destroyed the self-complementarity of the antennas, limiting the amount of impedance matching possible at the cost of low-frequency performance.
1. This photograph shows a prototype of the ATARSA.
To overcome these limitations, a new method was developed for tapering the arms of an ARSA while also preserving the self-complementarity of the design. Figure 1 shows an ATARSA, designed for an operating frequency range of 1.58 to 10.00 GHz; it has an outer diameter of only 53 mm. The small size is achieved by a combination of thin tapers and increased number of windings. The antenna is backed by an absorber-loaded cavity to enhance its unidirectional operation. This eliminates back-side radiation without decreasing the frequency band of operation, although at some loss of efficiency. An exponentially tapered microstrip balun is employed as a balanced feed for the antenna.
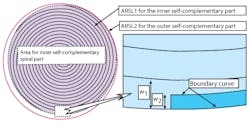
When an ATARSA is designed, the self-complementarity of an ARSA is maintained in a transition area (Fig. 2). Archimedean spiral curves are defined by the function r = r0 + aφ where r0 is the original radius of the spiral line, a is the spiral constant, and φ is the winding angle (derived from the starting angle, φst and the ending angle, φend). The width of the Archimedean spiral lines must be aπ/2 when a two-arm self-complementary ARSA is built.
In Fig. 2, the inner area is fully filled without any overlap by duplicating a self-complementary Archimedean spiral line (called ARSL1) at every 90-deg. rotation. The second self-complementary Archimedean spiral line, ARSL2, begins at the φend of ARSL1. Its outer boundary curve is flush with that of the inner area and its inner boundary curve is flush with the outer boundary curve of the inner winding area after a 90-deg. winding. In this way, it can fill the outer area. The width of ARSL2 (w2) is smaller than the width of ARSL1 (w1), so the arm width is tapered and the self-complementary structure of the ATARSA is preserved.
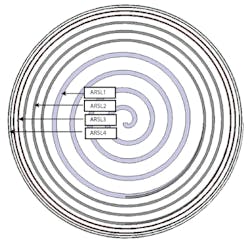
The miniature ATARSA was modeled by understanding its mechanical construction. Its antenna arms consisted of ARSLs with four different widths (Fig. 3). If these four ARSL “subantennas” are considered as ARSL1, ARSL2, ARSL3, and ARSL4, then ARSL1 was formed with four windings with width of 1 mm, ARSL2 was constructed with three windings 0.5 mm wide, ARSL3 with two windings each 0.25 mm wide, and ARSL4 with two windings each 0.125 mm wide. There were 11 windings in the antenna aperture, the outer diameter of which is 53 mm. To achieve good matching behavior, the original radius of ARSL1 was chosed as 1 mm. The ATARSA was fabricated from a circular substrate with relative dielectric constant of 4.3 in the z direction at 10 GHz and thickness of 1 mm.
4. These plots reveal (a) the impedances of the ATARSA and a typical ARSA and (b) the S11 behavior of the ATARSA with and without a balun.
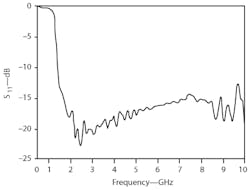
The characteristic impedance of a two-arm ATARSA simulated alone is shown in Fig. 4(a), together with the characteristic impedance of a typical self-complementary ARSA with arm width and outer diameter of are 1 mm and 53 mm, respectively. According to basic ARSA design principles, the wavelength of the lowest frequency of operation will be determined by the formula C ≥ 1.5λ, where C is the circumference of the antenna aperture and λ is the wavelength of the lowest operating frequency. By this formula, the lowest frequency of operation for the miniature ATARSA is 2.7 GHz. But from Fig. 4, it is possible to find that real and imaginary parts of the ATARSA’s impedance change more gradually over frequency than those of an ARSA. The imaginary part of the ATARSA’s impedance changes more approximately to zero, likely because of the better self-complementary structure of the ATARSA than the ARSA. As a result, the ATARSA provides excellent reflection coefficient characteristics with impedance chose for 100Ω across the full operating band [Fig. 4(b)]. An exponentially tapered microstrip balun was used as the feed for the ATARSA. Figure 4(b) shows the simulated results for S11 when the ATARSA is fed by that balun, with S11 better than −10 dB from 1.3 to 10.0 GHz.
The performance of the spiral antenna was evaluated by simulating and measuring its axial ratio, a parameter that assigns a value to the ratio of an antenna’s electric field strength in its two major axes. For an antenna with radiating field that is perpendicular to the direction of propagation, the electric field magnitude is generally reprsented by an ellipse which can be characterized by the axial ratio. An antenna’s polarization can be linear, circular, or elliptical where, in the first two cases, a plot of the antenna’s electric field appears as a straight line or a circle, respectively. The polarization in turn can be characterized as rotating in a clockwise direction, and being designated as right-hand polarization, or rotating in a counterclockwise direction, and being called left-hand polarization.
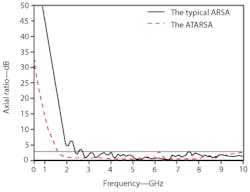
Figure 5 offers another comparison between the axial-ratio performance of a typical ARSA and the novel ATARSA. The ATARSA shows excellent performance in terms of circular polarization. According to the simulations of axial ratio, the ATARSA works well with circularly polarized signals in the frequency range from 1.4 to 10.0 GHz.
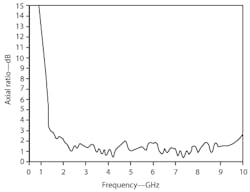
For the prototype, the ATARSA was etched onto a 1-mm-thick, copper-laminated dielectric substrate with permittivity of 4.3. The antenna was backed by a cavity full of microwave absorber material to improve directivity. Measurements were performed with a commercial microwave vector network analyzer (VNA), with results shown in Fig. 6. The measured results show good antenna performance from 1.4 to 10.0 GHz, correlating well with the simulated results.
7. The measured axial ratio of the ATARSA is shown here.
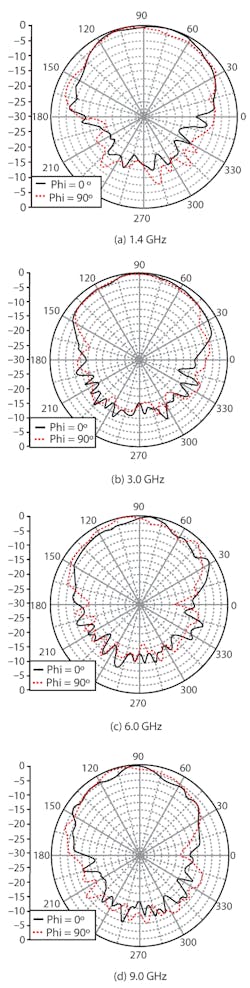
Figure 7 shows the axial ratio of the ATARSA in the main direction of radiation. The plot reveals the excellent broadband characteristics of the antenna. The VNA-measured results, while not exactly matching the simulated data of Fig. 5, do track the broadband axial-ratio behavior of the simulations, indicating stable performance from 1.4 to 10.0 GHz. Figure 8 shows radiation patterns for four different frequencies (1.4, 3.0, 6.0, and 9.0 GHz). The antenna design appears to do well with circular polarization, with reasonable performance at the low-frequency operating limit of 1.4 GHz. This compares to the lowest frequency of operation for a typical ARSA of about 2.7 GHz. The ATARSA essentially achieves a 73.1% reduction in antenna aperture area in contrast with a typical ARSA working in the same frequency band.
In conclusion, by tapering the arm width of the antenna along an increasing winding angle, it was possible to design a self-complementary Archimedean spiral antenna with miniature dimensions but with good low-frequency performance. This difficult-to-achieve low-frequency response combines with the antenna’s high-frequency capability for a continuous, wideband radiation pattern. The simulations and measurements of a prototype ATARSA shows excellent performance from 1.4 to 10.0 GHz, with significantly more effective miniaturization than reported in refs. 8-10.
Acknowledgments
The authors would like to thank the support from National Natural Science Foundation of China under Grant No. 60971118. Thanks are also due to the reviewers for their valuable comments.
References
1. B.A. Kramer, C.-C. Chen, and J.L. Volakis, “Size reduction of a low-profile spiral antenna using inductive and dielectric loading,” IEEE Antennas and Wireless Propagation Letters, Vol. 7, 2008, pp. 22-25.
2. Zhu Yu-xiao, Zhong Shun-shi, and Xu Sai-qing, “Miniaturized compound spiral slot antenna.” Microwave and Optical Technology Letters, Vol. 50, No. 11, 2008, pp. 2799-2801.
3. M.W. Numberger and J.L. Volakis, “New termination for ultra-wideband slot spirals,” IEEE Transactions on Antennas and Propagation, Vol. 50, No. 1, 2002, pp. 82-85.
4. H. Nakano, S. Sasaki, H. Oyanagi, et al., “Cavity-backed Archimedean spiral antenna with strip absorber,” IET Microwaves Antennas & Propagation, Vol. 2, No. 7, 2008, pp. 725-730.
5. H. Nakano, K. Kikkawa, Y. Iitsuka, et al., “Equangular spiral antenna backed by a shallow cavity with absorbing strips,” IEEE Transactions on Antennas and Propagation, Vol. 56, No. 8, 2008, pp. 2742-2747.
6. Hisamatsu Nakano, Tatsuya Igarashi, Hiroshi Oyanagi, et al., “Unbalanced-mode spiral antenna backed by an extremely shallow cavity,” IEEE Transactions on Antennas and Propagation, Vol. 57, No. 6, 2009, pp. 1625-1633.
7. J.A. Kaiser, “The Archimedean two-wire spiral antenna,” IRE Transactions on Antennas and Propagation, Vol. 8, No. 3, 1960, pp. 312-323.
8. Song Zhao-hui, Qiu Jing-hui, and Li Hong-mei, “Novel planar complex spiral ultra-wideband antenna,” 2004 4th International Conference on Microwave and Millimeter Wave Technology Proceedings. Beijing, 2004, pp. 35-38.
9. Zhu Yu-xiao, Zhong Shun-shi, Xu Sai-qing, and Zhang Li-na, “Design of miniaturized planar spiral antenna and its wideband balun,” Journal of Shanghai U., Vol. 14, No. 6, 2008, pp. 581-584.
10. Ya-wei Wang, Guang-ming Wang, and Zhong-wu Yu, “Design of a highly miniaturized compound spiral antenna,” 2010 ISSSE. Nanjing, pp. 494-496.