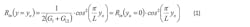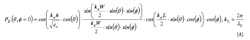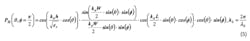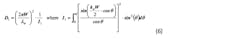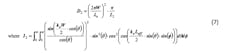Download this article in PDF format.
Picking up from where Part 1 left off, this article explores the single-element, rectangular microstrip antenna. Antenna arrays will be examined later in the series.
Microstrip Antenna Feed Line
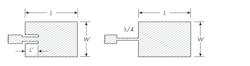
The resonant input resistance at the edge of the microstrip conductor is generally greater than the feed-line characteristic impedance and requires an impedance-matching structure to reduce the mismatch loss and thereby improve the antenna efficiency. Two common feed-line techniques can facilitate the impedance matching required to achieve an efficient rectangular microstrip antenna (Fig. 1).
1. Shown are the inset-feed (left) and quarter-wavelength (right) techniques for impedance matching.
The inset feed technique utilizes the reduction in electric-field strength to effectively “tap” a lower impedance drive point. The quarter-wave transformer uses the transmission line formula, which provides the geometric mean of the input resistance and the characteristic impedance of the quarter-wave transmission line. Coaxial probes beneath the conductor or a vertically offset feed along the width are also used on occasion.
A useful equation to achieve the optimum inset length, yo, is available:1
Although quite convenient and easily implemented, the inset feed distorts the equivalent slot radiation due to the change in geometry. The quarter-wavelength feed minimizes the equivalent slot field distortion due to the narrower, high-impedance line required for impedance matching. The simple formula for the impedance of the quarter-wavelength transmission line may be written as:
For a typical value of Rin = 200 Ω and Zin = 50 Ω:
Radiation Intensity Patterns
The two-slot radiation model is used to predict the E-plane and H-plane radiation patterns. The radiation intensity of the rectangular microstrip antenna of width W, length L, and height h, may be calculated using the following equations:2
For the E-plane radiation pattern: ø = 0 and −π/2 < θ < π/2 (planes have been redefined to comply with reference)
For the H-plane radiation pattern: ø = π/2 and − π/2 < θ < π/2 (planes have been redefined to comply with reference)
Bancroft3 provides reduced complexity expressions for the E-plane and H-plane radiation patterns. However, accuracy is modestly compromised due to elimination of the height, h, as a dependent variable.
Microstrip Antenna Directivity
The two-slot radiation model is also utilized to predict the directivity of the rectangular microstrip antenna. Figure 5 from Part 1 represents graphic definition in conjunction with the microstrip antenna dimensions as previously defined. Although the equation for directivity of a single slot requires the condition koh << 1, the expression provides reasonable accuracy upon comparison with actual measurement if the condition is moderately violated.
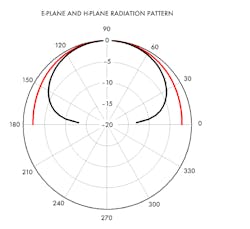
2. E-Plane (red) and H-Plane (black) radiation patterns are detailed.
The directivity of a single slot may be written:4
The directivity of a two-slot array, i.e., the microstrip antenna, may be written using the following expression:5
Microstrip Antenna Design
Although the previous text and equations have indicated a significant performance dependence on the width of the microstrip conductor, the astute reader may recognize that no guidelines or formulae have been offered for the width calculation. A practical starting point has been suggested by Bancroft in the following equation:6
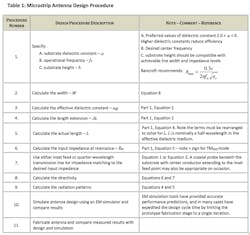
The procedure for the design of a single-element, rectangular microstrip antenna is summarized in Table 1.
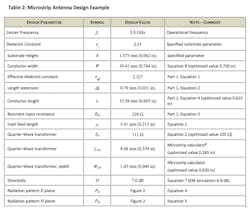
Microstrip Antenna Design Example
To summarize the rectangular microstrip antenna tutorial content at this point:
- Operational parameters and principles have been established.
- Design parameters and equations have been presented and references identified.
- Design procedure has been outlined.
To further explore the rectangular microstrip antenna, a design example7 is documented in Table 2 using the procedure of Table 1. The example illustrates the design procedure for a 5.8-GHz, direct-coupled microstrip antenna on 0.062-in.-thick Rexolite (www.rexolite.com) substrate. Rexolite is a dimensionally stable, cross-linked polystyrene plastic with a frequency-independent dielectric constant of 2.55 and low loss tangent (typically less than 0.001 to 100 GHz).
Fig. 2 represents the E-plane and H-plane radiation patterns of the 5.8-GHz, rectangular microstrip antenna. Note that the beamwidth of the E-plane radiation pattern is somewhat greater than the H-plane beamwidth. It should also be noted that the H-plane radiation pattern is independent of the slot separation length, L. This is not evident from Equation 5 until one cautiously considers the equation under the condition, ø = π/2.
The E-plane and H-plane radiation patterns of Fig. 2 were calculated with MathCad using the equations of Reference 4 from Part 1. Similar patterns are produced using the other cited references.
EM Simulation of Direct-Coupled Microstrip Antenna
Although the design equations provide the initial dimensional data and radiation patterns for the microstrip antenna design, an electromagnetic (EM) simulation is generally required to reduce the number of prototype iterations and achieve the available performance objectives. To that end, an EM simulation of the 5.8-GHz, direct-coupled microstrip antenna was executed using the AXIEM 3D planar EM simulator within the NI AWR Design Environment.9
Results of the direct-coupled microstrip antenna EM simulation are summarized within the graphics of Table 3 and represent a degree of dimensional optimization of the initial design values as previously indicated.
In addition to providing the ability to optimize antenna performance, the AXIEM simulation software also enables dimensional sensitivity analysis; e.g., as one might expect, the length of the microstrip conductor (L) was found to significantly influence input impedance and center frequency. The microstrip conductor width (W) was found to have influence on the directivity and was useful in optimizing the input impedance. The substrate thickness (h) was found to be the principal determinant to bandwidth and efficiency.
The value of EM antenna simulation is manifest in the ability to optimize performance as well as to provide physical insight to antenna operation using conductor current and electric-field annotation capabilities. Note specifically the current density at the conductor edges. One might correctly consider that the radiation properties of the microstrip antenna may also be explored using the current density. In fact, the radiation patterns of the microstrip antenna could also be calculated using the vector potential associated with the conductor current.
Prototype Microstrip Antenna
A prototype microstrip antenna was fabricated in accordance with the parameters of Table 2 with modest dimensional revision resulting from the EM simulation to optimize the input impedance and directivity. The prototype antenna conductor dimensions are illustrated in Figure 3.
3. This is the microstrip antenna conductor pattern for the 5.8-GHz design example.
References
- Balanis, C. A., Antenna Theory, 3rd Ed., John Wiley and Sons, Hoboken, NJ, 2005, pp. 824-825.
- Carver, K. and Mink, J., Microstrip Antenna Technology, IEEE Transactions, Antennas and Propagation, January 1981.
- Bancroft, R., Microstrip and Printed Antenna Design, 2nd Ed., Scitech Publishing, Raleigh, NC, 2009, p. 30.
- Balanis, C. A., Antenna Theory, 3rd Ed., John Wiley and Sons, Hoboken, NJ, 2005, p. 840.
- Balanis, C. A., Antenna Theory, 3rd Ed., John Wiley and Sons, Hoboken, NJ, 2005, p. 841.
- Bancroft, R., Microstrip and Printed Antenna Design, 2nd Ed., Scitech Publishing, Raleigh, NC, 2009, p. 60.
- An excellent design example of a 10-GHz microstrip antenna is presented in [6], Chapter 14.
- Online microstrip parameter calculator: http://www.microwaves101.com/content/calculators.cfm.
- AXIEM technology utilizes an open-boundary, non-gridded, method-of-moments solver that supports thick metal in layered dielectric media. Additional information is available at awrcorp.com/products/axiem.