Temperature Sensing Stabilizes MCXO
This file type includes high resolution graphics and schematics.
Temperature challenges the accuracy and stability of even the best-made crystal oscillators. For that reason, a precision temperature sensor is typically part of any high-precision quartz frequency source, helping to provide compensation for the effects of changes in temperature. In a temperature-compensated crystal oscillator (TCXO), for example, a thermistor is used in close proximity to the oscillator’s resonator, which is usually an AT-cut quartz crystal. Unfortunately, this temperature-correction approach suffers from inaccuracies due to thermal lag stemming from a difference of effective thermal time constants in crystal and thermistor, thermal gradients, and thermistor aging.1
Related Articles
• Make Sense Of Sensing
• Minimize Power In Wireless Sensing
• Energy Harvesting Is Ready For The Big Time
Another method for overcoming these limitations is resonator self-temperature-sensing using a dual-harmonic-mode crystal oscillator.2 This method provides for the resonator to determine its own temperature reading (rather than using external temperature sensors), and yields high-precision microcomputer-compensated crystal oscillators (MCXOs) with better precision than any other TCXO. Unfortunately, the large size of these sources, the high cost of SC-cut crystal, and the complicated dual-harmonic-mode oscillator structure of the MCXO prevent it from being widely used in electronic products.
A dual-AT-cut-crystal oscillator structure with self-temperature-sensing was first proposed in ref. 3. The current authors’ experimental results prove that this method has nearly the same level of precision as the dual-harmonic-mode resonator self-temperature-sensing. With increasing progress towards ultrasmall crystal units,4 this method is particularly well suited for application in miniature MCXOs. In the present report, a MCXO using a dual-AT-cut-crystal self-temperature-sensing circuit was developed, capable of providing frequency-temperature stability of better than 0.1 ppm, with smaller size and lower cost than conventional MCXO5,6 by employing AT-cut crystals.
1. Frequency-temperature characteristics of AT-cut crystal.
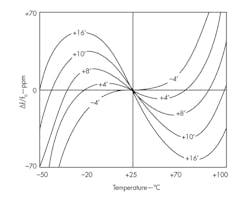
An AT-cut crystal for use as a resonator in an oscillator is typically cut around a nominal angle of +35○15’. Furthermore, its frequency-temperature (F-T) characteristic, which can be generally expressed in terms of Eq. 1, depends on the precise shearing angle (Fig. 1):
Δf/f0 = a + bΔT + cΔT2 + dΔT3 (1)
where the normalized frequency, Δf/f0, and the difference temperature, ΔT, are referenced at room temperature. Comparing the cut angle of (+35○15’) + 16’ with (+35○15’) - 4’, the difference between the two normalized frequencies has a monotone decreasing from +1.10 x 10-4 to -1.05 x 10-4 in the temperature range from -40 to +85°C. When the baseline frequency is 10 MHz, the differential frequency range will be 2150 Hz, which means that the average temperature-frequency sensitivity is 0.058○C/Hz, and nearly equal to the dual-harmonic-mode resonator self-temperature-sensing.
2. Frequency-temperature characteristics of two different shearing angle AT-cut crystals.
The F-T characteristics of two AT-cut 10-MHz quartz crystals with shearing angles of (+35○15’)+4’ and (+35○15’)−2’ are shown in Fig. 2, and their difference frequency characteristic can be described by Eq. 2 as:
Δf1(ΔT) - Δf2(ΔT) = -60.584 + 2.00948 x ΔT + 0.001977 x ΔT2 + 0.00000424 x ΔT3 ≈ -60.584 + 2.00948 x ΔT (2)
which means that the temperature-frequency sensitivity of this dual-resonators temperature sensor is 0.4976○C/Hz. When the frequency resolution of this sensor is 0.1 Hz, its temperature resolution will be 0.04976○C and it will be free of thermal lag in terms of temperature compensation.
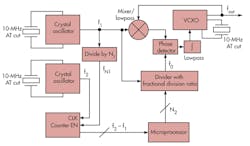
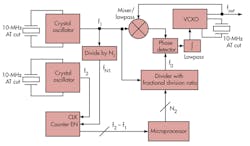
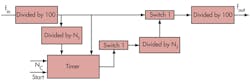
3. Architecture of the MCXO with the dual-crystals self-temperature-sensing.
Figure 3 shows the basic architecture of the MCXO with a dual-AT-cut-crystal resonator and self-temperature-sensing approach. For the differential frequency measurement, one of the oscillator’s outputs, f1, is divided by the fixed value, N1, to obtain a signal fN1 for gating a counter, which is fed from the other oscillator’s output, f2. The counter produces a count value, C1, during a period of fN1, according to the relationships of Eq. 3:
N1(1/f1) = C1(1/f2) (3)
In 10-MHz crystals, the deviation range of f2 is typically less than 1 kHz or, as shown by Eq. 4:
[(C1 - N1)/C1]107 = [(f1 - f1)/f2]107 ≈ f2 - f1 (4)
The computation of differential frequency between f2 and f1 has a relative precision to 10-4, which means a measurement accuracy of at least 0.1 Hz. The divisor N1 serves to scale the C1 counter range consistent with the required temperature-sensing resolution and counter width.
4. Block diagram of the divider with fractional division ratio.
The differential frequency is read by the microprocessor to determine the actual frequency of f1 via the polynomial computation of Eq. 1, the coefficients of which are derived from a least-squares curve-fitting routine using data taken during a frequency-temperature characteristic measurement. The predicted frequency is subtracted from the target 10-MHz frequency to determine the deviation, Δf1. The deviation Δf1 of approximately 400 Hz is generated from f0 by a divider with a fractional division ratio as shown in Fig. 4. The microprocessor then computes a fractional division ratio, NC as in Eq. 5, which is used to control the fractional divider to produce a correction frequency equal to Δf1. A voltage-controlled crystal oscillator (VCXO) is employed to establish the target 10-MHz frequency, in which the output frequency of VCXO is phase-locked to the sum of f1 - Δf1:
fout = (fin/10000)(1- NC/N2N3) (5)
This file type includes high resolution graphics and schematics.
The Small Print
This file type includes high resolution graphics and schematics.
Related Articles
• Make Sense Of Sensing
• Minimize Power In Wireless Sensing
• Energy Harvesting Is Ready For The Big Time
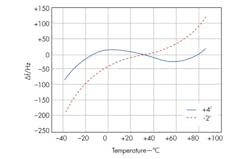
The proposed MCXO circuit was fabricated in a 0.18-μm, 1.8-VDC silicon CMOS process; it features power consumption of less than 5 mW. It can achieve frequency stability within ±0.1 ppm over a range of temperatures from -40 to +85°C. Figure 5 shows the frequency deviation for two repeated cold to hot and hot to cold temperature runs for one proposed MCXO, which is better than for a conventional TCXO.5,6 For all temperature runs, the protocol initiated with a 10 minute “soak” time followed by a change of 1°C every minute. The entire testing process was automated including protocol control and data collection.
5. Frequency stability under temperature tests.
By employing ultrasmall AT-cut crystal units, the proposed MCXO has a smaller size of 13 x 13 x 1.75 mm, comparing with a traditional MCXO using SC-cut dual-mode crystal,7 which has a size of 38.1 x 38.1 x 12.7 mm, making the proposed MCXO more suitable for applications in portable productions.
Liang Chen, Engineer
Yangbo Huang, Engineer
Yonghu Zhang, Engineer
Gang Ou, Engineer
College of Electronic Science and Engineering, National University of Defense Technology, Changsha, Hunan, China, People's Republic of China.
References
1. S.S. Schodowski, “Resonator self-temperature-sensing using a dual-harmonic-mode crystal oscillator,” in Proceedings of the 43rd Annual Symposium on Frequency Control, Denver, CO, May 31-June 2, 1989, pp. 2-7.
2. A. Benjaminson and S. C. Stallings, “A Microcomputer-Compensated Crystal Oscillator Using a Dual-Mode Resonator,” in Proceedings of the 43rd Annual Symposium on Frequency Control, Denver, CO, May 31-June 2, 1989, pp. 20-27.
3. T. Schmid, J. Friedman, Z. Charbiwala, Y. H. Cho, M. B. Srivastava, "XCXO: An Ultra-low Cost Ultra-high Accuracy Clock System for Wireless Sensor Networks in Harsh Remote Outdoor Environments," 2007.
4. M. Harada, K. Kubota, and H. Takahashi, “Research on Miniaturization of Low-Frequency Range SMD Crystal Unit," in Proceedings of IEEE International Frequency Control Symposium, 2007, pp. 150-153.
5. H. Rokos, "Precision, Low Power, analogue TCXO using a Single Integrated Circuit," in Proceedings of European Frequency Time Forum, 1996, pp. 515-519.
6. Mi Zhang, Wei-xun Cao, “A 0.1 ppm Successive Approximation Frequency-Temperature Compensation Method for Temperature Compensated Crystal Oscillators (TCXO),” in Proceedings of World Congress on Computer Science and Information Engineering, 2009, pp. 493-498.
7. E. Jackson and B. Rose, “The microprocessor compensated crystal oscillator-new developments,” in Proceedings of IEEE International Ultrasonics, Ferroelectrics, and Frequency Control, 1999, pp. 376-379.
This file type includes high resolution graphics and schematics.