Algorithms to Antenna: Synthesizing an Antenna Array with Optimization Techniques
In this blog, I describe array-synthesis techniques for phased-array antennas—in each case, the design starting point is an array pattern that satisfies certain performance criteria. These criteria can include parameters such as main-lobe directivity and beamwidth, null locations, and side-lobe levels.
As noted in my second and seventh blog posts, massive-MIMO arrays may include hundreds or even thousands of elements. It can take many iterations to converge on an array architecture to achieve a specific pattern. These iterations take time and are difficult to complete thoroughly when multiple parameter sweeps need to be considered.
Optimization techniques greatly increase the efficiency of the array-synthesis process. You can evaluate a pattern over a range of weights and element positions; each iteration of the automated process is usable to evaluate how a generated pattern compares with the desired pattern. To ensure that the solution meets design goals, it’s important to understand design options and to know which constraints must be accounted for.
The parameters that most influence the array pattern include the number of elements in the array, the lattice structure of those elements, and the array geometry. Within the array, parameters associated with each element determine the beam-pattern characteristics, including the weights applied to each element (amplitude or phase) and the element’s location within the array. These parameters serve effectively as “knobs” that you can turn to meet performance goals.
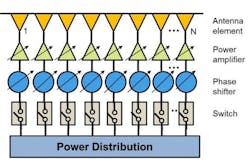
1. Shown is a flexible phased-array architecture.
For multi-element arrays, the degrees of freedom in the design will vary based on the cost and complexity constraints of the end application. In the most basic systems, amplitude-only weights are available. However, many architectures support complex weighting for elements or subarrays, providing both amplitude and phase control. With this type of architecture, the beam can be steered and shaped electronically (Fig. 1).
The array geometry in a design is usually driven by the constraints of the end-system form factor, but the spacing between individual elements may be flexible. This flexibility is constrained by what can actually be manufactured. If elements are too close together, they will not be realizable when going through the manufacturing process.
I will describe two examples. In the first, the array is an 8-element linear array with uniform spacing. The goal is to generate a set of element weights that can be applied to achieve a desired pattern. In the second example, I build a planar array where the element weights and element positions will converge to achieve a set of array performance objectives.
Optimizing Weights Only
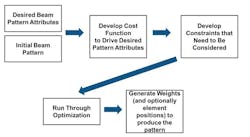
This example follows the steps shown in Figure 2 to generate antenna-element array weights.
2. Here are workflow steps for optimizing weights.
Starting with a 2D pattern that’s specific to a set of azimuth and elevation angles, a cost function can be developed to minimize the distance between the desired pattern and the pattern generated from the weighting vector.
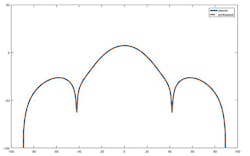
To determine the element weights, the distance between the two beam patterns is minimized. An objective function is defined such that it iteratively refines the difference between the starting pattern and the pattern generated as the weights converge. At the end of the optimization, a set of weights is produced so that when applied to the array elements, a match to the desired pattern is obtained. The plot in Figure 3 shows the magnitude of both the desired and synthesized patterns over azimuth angles. In this figure, you can see the synthesized pattern matches the desired pattern.
3. The plot compares desired and synthesized patterns after optimization.
Optimizing Both Weights and Element Position
The second example follows the steps shown in Figure 4.
4. These workflow steps are followed to optimize both weights and element position.
I now control the amplitude, phase, and the 2D position of each element. Our goal for this optimization is to reduce the maximum side-lobe level of the pattern. We need to ensure that the element locations computed by the optimization process are not spaced too closely together.
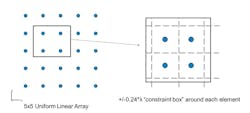
The array on the left side of Figure 5 shows the initial positions of the elements, which are uniformly spaced. For the lower and upper bounds for the y-z plane element positions, we set up a grid using (±0.24 × lambda) spacing from a uniform rectangular-array starting point (Fig. 5, right).
5. Shown on the left is a uniform linear array (5x5 elements). On the right is a corresponding “constraint box” around each element.
Once the array is set up, I determine the beam patterns across both the azimuth and elevation angles. This data is used to extract key metrics associated with the pattern. Here, I focus on the side lobes, but many other parameters could be considered, such as the main-lobe gain or the 3-dB beamwidth. There can be more than one main lobe as well.
Figure 6 shows the resulting polar pattern in the azimuth plane (left plot) and the elevation plane (right plot). In both plots, the starting point pattern is the blue line, and the optimized pattern is the orange line. This optimization focused on reducing sidelobe levels; you can see the reduction in both azimuth and elevation.
6. Depicted on the left is a polar pattern in the azimuth plane showing the starting point pattern (blue line) and the optimized pattern (orange line). The right side illustrates corresponding views for the elevation plane.
The new patterns are generated using the weights and element positions returned from many iterations through the optimization function. Figure 7 shows the resulting array element positions and beam pattern.
7. This is the resulting array and beam pattern after optimization.
Extending the Examples
In these examples, all analysis was done at a single frequency value. In reality, systems have to work across a range of frequencies. Similar techniques can be applied across frequencies. For a wideband application, you can look at multiple frequencies equally spaced across the band. The decision then becomes: Which aspect of the application is most important? For example, it may be best to optimize for a specific combination and select the positioning based on this combination.
If having a set performance requirement for all combinations of frequencies is more important, the optimization can be adjusted accordingly. The optimization could also be extended to help drive an optimal subarray architecture across a set of steering vectors.
In addition to expanding the optimization to cover wider frequency ranges, phased-shift quantization effects can be added to the model to ensure that the end system will behave as is indicated by the simulation. This is important to help ensure that the results coming from the optimization can be built.
To learn more about the topics covered in this blog, see the links below or email me at [email protected].
- Array Synthesis Code (example code): Example code for optimization techniques to synthesize the arrays described in this blog.
- Array Pattern Synthesis (example): Learn to design a phased array to match a desired beam pattern to a specification.
- Hybrid Beamforming for Massive MIMO Phased Array Systems (white paper): Learn how to design hybrid beamforming in massive-MIMO antenna arrays for 5G.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
About the Author
Rick Gentile
Product Manager, Phased Array System Toolbox and Signal Processing Toolbox
Rick Gentile is the product manager for Phased Array System Toolbox and Signal Processing Toolbox at MathWorks. Prior to joining MathWorks, Rick was a radar systems engineer at MITRE and MIT Lincoln Laboratory, where he worked on the development of several large radar systems. Rick also was a DSP applications engineer at Analog Devices, where he led embedded processor and system level architecture definitions for high performance signal processing systems used in a wide range of applications.
He received a BS in electrical and computer engineering from the University of Massachusetts, Amherst, and an MS in electrical and computer engineering from Northeastern University, where his focus areas of study included microwave engineering, communications, and signal processing.