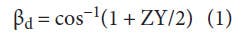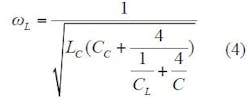Novel Transmission Line Impacts Antenna Design
This file type includes high resolution graphics and schematics when applicable.
Demand for electrically small antennas continues to soar, particularly among mobile electronic applications. Though the benefits are significant, these antennas aren’t the easiest to achieve. Use of a novel composite-right/left-handed (CRLH) transmission line, however, facilitates the creation of these antennas. A CRLH transmission line incorporates a ground plane with an etched complementary single split-ring resonator (CSSRR) and a patch with two series gaps and two metal viaholes.
Based on a CRLH transmission-line unit cell, an antenna was designed and fabricated, and found to provide a –10-dB impedance bandwidth of 5.63% at 3 GHz. The compact antenna patch measures only 0.2 λ0 × 0.17λ0 × 0.01λ0—a 69.1% reduction in size compared to a conventional patch antenna. The compact antenna design achieved peak gain of 4.29 dB.
Some of these electrically small antennas exploit the electromagnetic (EM) characteristics of CRLH transmission lines. Since the realization of resonant frequency of a zeroth-order resonator (ZOR) is independent of its dimensions, but is determined by the configuration of the unit cells, there’s been a spate of ZOR-based miniaturized antennas proposed of late.1 Unfortunately, they’re often limited in terms of bandwidth.
By combining a TM010 transmission mode and a ZOR mode, however, some antennas increased half-power beamwidth by 53% over conventional rectangular patch antennas, with a boost in antenna bandwidth of 3.3%.2 In one study,3 a hybrid mode was proposed in which a wideband patch antenna with TM01 and TM10 modes was loaded with a planar CRLH unit cell to enhance its bandwidth, but its size only shrank by 45% compared to a conventional rectangular patch antenna.
CRLH Transmission-Line Innovation
To maintain antenna performance with reduced size, a new type of CRLH transmission-line structure was developed. It reduces the resonant frequency by loading with a complementary single split-ring resonator (CSSRR) for shunt inductance and a patch slot for series capacitance. Also, two symmetric viaholes were added to change the shunt inductance. These techniques made it possible to implement a CRLH unit cell in fully planar technology, toward the design of a compact antenna.
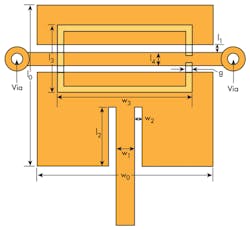
Figure 1 shows the geometry of the proposed antenna. A patch with two series gaps and two short stubs is formed on the top side, and a CSSRR slot is etched on the ground plane on the bottom side. The two white circles denote metallic viaholes.
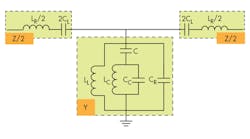
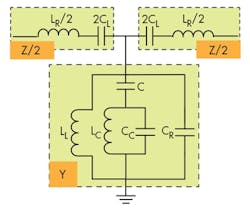
According to CRLH transmission-line theory, the equivalent-circuit model of the proposed antenna can be depicted as that in Fig. 2. Since the patch provides series inductance and the gaps yield series capacitance, the patch with two series gaps is represented as a series LC circuit (LR and CL), while the CSSRR slot is represented as a shunt LC resonant tank (CC and LC).4 On the other hand, the capacitance between the patch and the ground plane capacitance (C) connects the shunt resonant tank to the patch, while capacitance CR connects the ground with the patch. The two metallic viaholes connected with two short stubs are described by shunt inductance LL, connecting the patch with ground.
Based on the analysis above, one can safely conclude that a model circuit is provided by a complex CLRH transmission-line circuit: CL represents the left-handed capacitance; LC and LL represent the left-handed inductance; C and CC represent the right-handed capacitance; and L is the right-handed inductance. From the equivalent-circuit model, the dispersion relation can be expressed as Eq. 1:
where
βd = the length of the unit cell,
and
Z = jωLR + 1/(jωCL)
and
Y = [jωC/(jωC + 1/jωLC)] + 1/jωLL)] + jωCR
represent the series impedance and shunt admittance, respectively. The dispersion relation can be determined by means of Eq. 2:
In another way, it’s possible to obtain the resonant modes of the CRLH transmission line by applying Eq. 3:
With these relationships, the negative first-order resonance, the ZOR, and the positive first-order resonance can be obtained according to Eqs. 5 and 6. At the ZOR, the phase constant, βd, becomes zero and infinite wavelength propagation is theoretically possible, although the working bandwidth is narrow. The negative first-order resonance supports backward-wave propagation with the same field distribution as the positive first-order resonance, but generally has such low efficiency that it cannot be used for antenna radiation purposes.5
This file type includes high resolution graphics and schematics when applicable.
Antenna Analysis
This file type includes high resolution graphics and schematics when applicable.
Analyzing the antenna design can be somewhat complicated. Considering the shunt part, there are four relevant resonant frequencies relative to the shunt impedance based on this circuit model: two frequencies that null the corresponding admittance (ωC and ωL), a shunt resonant frequency (ωsh), and a transmission-zero frequency (ωZ). Parameters ωC, ωsh, ωZ were previously explained in Eq. 3, and the relationship for ωL is given in Eq. 46,7:
The resonant efficiency is low at ωsh and the right-handed resonant efficiency (ωR) is often higher than in practice applications.
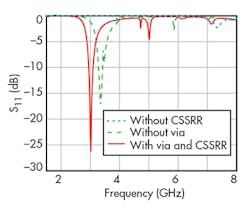
Figure 3 compares reflection coefficients (S11) for the proposed antenna without CSSRR, without viaholes, and with CSSRR and viaholes. The antenna with viaholes and CSSRR achieves a multiple-resonant frequency response with reduced frequency compared to the other two approaches.
For the best radiated performance, the antenna dimensional parameters were optimized for the following values:
w0 = 20 mm; w1 = 2.72 mm; l0 = 17.4 mm; l1 = 0.5 mm;
g = 0.8 mm; w2 = 0.3 mm; l2 = 6.1 mm;
w3 = 22 mm; l3 = 14 mm; and l4 = 0.8 mm.
The radius of the viahole was 0.15 mm.
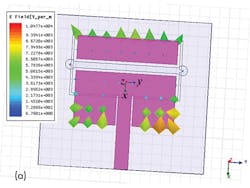
The simulated electric-field distributions for the proposed compact antenna are depicted in Fig. 4(a). With the structure’s two x-oriented edges being 180 deg. out of phase at 3 GHz, a transverse-magnetic TM10 mode is excited. The simulated gain for the antenna at 3 GHz is given in Fig. 4(b), with full orientation in the Y0Z plane and maximum gain at 4.29 dB. Figure 5 shows the prototype of the proposed antenna fabricated on the Teflon substrate with relative dielectric constant of 2.65.
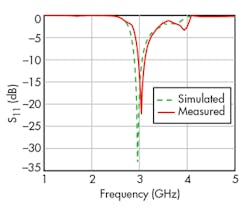
Figure 6 illustrates simulated and measured reflection coefficients of the proposed antenna. The measured data were in good agreement with the simulated results, with just a few exceptions. The measured 10-dB return-loss bandwidth was 170 MHz (5.6%) from 2.94 to 3.11 GHz. The electrical size of the radiating patch was 0.2λ0 × 0.17λ0 × 0.01λ0 (20 × 17.4 × 1 mm) at a center frequency of 3.02 GHz.
Owing to the CRLH structure and use of metal viaholes to enhance the shunt inductance, antenna size was reduced 69.1%, compared to a conventional patch antenna measuring 37 × 30.4 × 1 mm. Even with this dramatic size reduction, the microstrip patch antenna provides strong performance at its 3.02-GHz center frequency.
Acknowledgment
This work is supported by the National Natural Science Foundation of China under Grant No. 61372034.
Tian-Peng Li, Engineer
Guang-Ming Wang, Engineer
Chen-Xin Zhang, Engineer
Bin-Feng Zong, Engineer
Air and Missile Defense College, Air Force Engineering University, Xi’an, Shaanxi 710051, China
References
1. T. Ueda, G. Haida, and T. Itoh, “Zeroth-order resonators with variable reactance loads at both ends,” IEEE Transactions on Microwave Theory & Techniques, Vol. 59, No. 3, 2011, pp. 612–618.
2. S.T. Ko and J.-H. Lee, “Hybrid zeroth-order resonance patch antenna with broad E-plane beamwidth,” IEEE Transactions on Antennas & Propagation, Vol. 61, No. 1, 2013, pp. 19–25.
3. J. Ha, K. Kwon, Y.K. Lee, and J. Choi, “Hybrid mode wideband patch antenna loaded with a planar metamaterial unit cell,” IEEE Transactions on Antennas & Propagation, Vol. 60, No. 2, 2012, pp. 1143-1147.
4. M. Gil, J. Bonache, J.G. García, J. Martel, and F. Martín, “Composite right/left-handed metamaterial transmission lines based on complementary split-ring resonators and their applications to very wideband and compact filter design,” IEEE Transactions on Microwave Theory & Techniques, Vol. 55, No. 6, 2007, pp. 1296–1304.
5. C. Zhou, G. M. Wang, Y.W. Wang, B.F. Zong, and J. Ma, “CPW-fed dual-band linearly and circularly polarized antenna employing novel composite right/left-handed transmission-line,” IEEE Transactions on Antennas & Propagation Letters, Vol. 12, 2013, pp. 1073-1076.
6. Ozgur Isik and Karu P. Esselle, “Backward Wave Microstrip Lines With Complementary Spiral Resonators,” IEEE Transactions on Antennas & Propagation, Vol. 56, No. 10, 2008, pp. 3173-3178.
7. M. Gil, J. Bonache, J. Selga, J. García-García, and F. Martín, “Broadband Resonant-Type Metamaterial Transmission Lines,” IEEE Microwave and Wireless Component Letters, Vol. 179, No. 2, 2007, pp. 97-99.
This file type includes high resolution graphics and schematics when applicable.