How to Improve Noise-Figure Measurements and Calibrate High-Power Noise Sources
Download this article in PDF format.
Those who have ever tried to manually measure an amplifier’s noise figure may have found that the numbers aren’t quite what was expected. This is most likely the result of the spectrum analyzer’s noise figure, which adds noise to the measurement. If an interfacing amplifier is needed to boost the device-under-test (DUT) output noise power above that of the spectrum analyzer’s noise floor, then it becomes even more likely that accuracy will suffer.
Additional components are sometimes necessary, but to accurately determine the noise figure of the DUT, one must know the gain and noise figure of the additional components so that the DUT characteristics can be de-embedded from the measured response. Although high-gain amplifiers are less susceptible to the analyzer’s noise figure, some analyzers can have extremely high noise figures at high frequency—on the order of 30 to 60 dB.
In addition to measuring noise figures, sometimes a calibrated high-power noise source is needed when the noise source is built into a system that contains substantial insertion loss in the RF path. This insertion loss is caused by some combination of couplers, splitters, filters, and/or lengths of coaxial line.
If one could build a perfect RF noise-power measurement instrument that contributed no additional noise to the input noise to be measured, then the two tasks described above would be accomplished. A noiseless measurement instrument is not yet available to the general public.
However, the next best solution does exist: an everyday spectrum analyzer, a calibrated noise source, and a couple of algebraic equations. With these tools, one can measure an unknown noise source within the accuracy of a calibrated reference. This article reveals how to construct this almost ideal test instrument.
Basics of the Ideal Measurement Instrument
The hardware consists of a preamplifier, interconnecting cable, and spectrum analyzer. There may even be a coaxial cable at the input to the preamplifier, but one is not included in this discussion. Adding an input cable doesn’t change the results of the analysis, since as we shall see, the interfacing component characteristics do not enter into the measurement calculations.
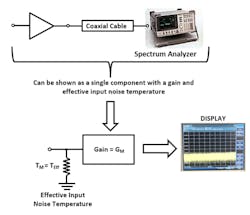
The components do have to be selected to work well at the measurement frequency, though. In addition, the preamplifier must be chosen so that with its input terminated, the output noise power is higher than the spectrum analyzer’s noise floor. The measurement circuit can be represented as a black box with gain (GM), effective input noise temperature (TM), and the display.
Eradicate Measurement Circuit Effects
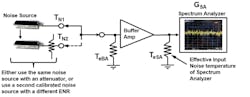
Eliminating the test circuit effects on the measured noise power from the DUT requires that we make two additional measurements without the DUT. Figure 2 shows the required measurements. They consist of two noise reference sources measured at the input to the test measurement circuit. The noise sources can be two separate sources, or one source with the second source made up of the first source with an accurately known attenuator on its output.
1. This is a representation of the measurement test circuit.
2. These measurement tests are required to eliminate test equipment effects on the DUT noise power measurement.
The black box representation shown in Figure 1 allows us to simplify the analysis. Furthermore, we can write much more efficient equations that enable the determination of the actual noise power present at the input of the test circuit.
If we terminate the input to the test circuit with two noise sources of different excess noise ratio (ENR), then the two corresponding equations for the displayed noise power are:
In the equations, TN1 and TN2 are the two noise-source temperatures. GM and TM are the equivalent measurement circuit gain and noise temperature parameters, respectively.
We now form two Y-Factors using the powers given in Equation 1 with the output power from the DUT, which we will denote as TUNK.
Note: A Y-Factor is simply the ratio of two power measurements as read on the spectrum analyzer. It can be stated as either a numerical ratio, or as dB. The context will dictate which one is used.
The two Y-Factor equations are:
Here, we have shown two Y-Factors, one being the ratio of the measured output power with the first noise source (we’ll call it noise source #1) to the output power with the unknown noise power source. The other is the ratio of the measured output power with the second noise source (noise source #2) to the output power with the unknown noise power source.
We rearrange equations 2 and 3 as such:
Rearranging:
Let k1 = Y1 − 1 and k2 = Y2 − 1. We also let m1 = k1 × Y2 and m2 = k2 × Y1.
If one uses the subtraction method and makes the above substitutions (for simplification), the result is:
All variables in this equation are either measurement quantities, or noise temperature values (related to the noise power by P = kTB) given by the manufacturer of the calibrated noise source. From this equation, we can calculate the noise temperature out of the DUT without knowing the gains and noise figures of the components in the test-measurement circuit.
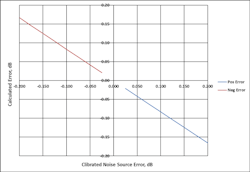
If we use the thermal model to examine the error associated with the error of the calibrated noise sources, we see that the overall error is essentially the same as the noise sources (Fig. 3).
3. Shown is the measurement error associated with noise-source error.
Applying to Real-World Problems
Now that we have a measurement tool that can measure the precise power level of an unknown noise source (ignoring the error associated with the calibrated noise source), we can apply it to the two original problems.
Noise-Figure Measurement
Noise Factor (which is related to the noise figure by: NFac = 10(NFig/10)) is defined by Equation 9, which states that the noise factor of a component is equal to the Enr (Enr = 10(ENR/10), where ENR is in dB) of the calibrated noise source divided by the measured quantity “Y-Factor-1.” In this context (classical noise-figure measurement method), Y-Factor is the ratio of the DUT’s output power with a calibrated noise source connected to its input (this is called the hot noise source) to the DUT’s output power when its input is terminated with a matched load (this is called the cold noise source).
This formula is valid when the noise out of the DUT significantly dominates all of the noise contributions of the test-measurement circuit. This will hardly be the case, which leads to the many accuracy issues that can arise. If we use the noise-power measurement technique discussed in this article, we can measure the output power of the DUT for the hot/cold conditions and precisely determine the ratio at the output of the DUT.
The two unknown temperatures, represented by the TUNK in Equation 8, are:
• Output from the DUT with a cold noise termination = TUC
• Output from the DUT with a hot noise termination = TUH
Now that we have measured the appropriate Y-Factors to calculate the output noise powers out of the DUT, we can calculate the noise factor of the DUT from the classic formula given in Equation 8:
From which the noise figure follows:
Noise-Figure Measurement Summary
To summarize the process, we need to make four noise power measurements read on the spectrum analyzer:
- A calibrated noise source connected directly to the test measurement circuit input. This would be connected to the buffer amplifier shown in Figure 2. Call this P1.
- A second calibrated noise source (or the first source with a high precision, measured attenuator at its output) connected to the buffer amplifier shown in Figure 2. Call this P2.
- The DUT with its input terminated in a matched load (290K) connected to the test circuit. Call this P3.
- The DUT with its input terminated with a calibrated noise source connected to the test circuit. Call this P4.
Next, to calculate the power coming out of the DUT, we form four Y-Factors:
- Y1 = P1/P3
- Y2 = P2/P3
- Y3 = P1/P4
- Y4 = P2/P4
Using Equation 8 and Y1, Y2, TN1, and TN2 to calculate k1, k2, m1, and m2, we calculate the temperature out of the DUT for the cold noise case. Call this T1.
Using Equation 8 and Y3, Y4, TN1, and TN2 to calculate k1, k2, m1, and m2, we calculate the temperature out of the DUT for the hot noise case. Call this T2.
Form the Y-Factor, Y5 = T2/T1
Using the classical Equation 9, we obtain the result:
where Enr is the excess noise ratio of the calibrated noise source used for the hot source into the DUT.
The entire process can be accomplished by using a single calibrated noise source. It’s worth mentioning that the attenuator used to create a lower Enr noise source needs to be accurately measured. Any error in this measurement will propagate to the results. Fortunately, high-accuracy attenuation measurements can easily be made with today’s test equipment.
One last important note: While it’s true that the exact component characteristics of the interfacing amplifier, cables, and spectrum analyzer are not used in the calculations for the DUT noise figure, one still must be careful choosing the components of the measurement circuit. The measurement circuit must be constructed such that a 290 Kelvin termination at the input to the DUT is above the spectrum analyzer’s noise floor relative to when the test circuit is terminated in a matched load (290 Kelvin). There’s no restriction on how far above the test circuit noise floor it must be—it just must be measurable.
This is the issue addressed by this article, which presents a method that eliminates the effects of the analyzer and its connecting circuitry. The result is a noise-figure measurement of the DUT irrespective of the circuitry on its output.
High-Power Noise Source
Applying the measurement technique to calibrate a high-power noise source should be clear at this time from the above discussion, but it will be briefly explained.
Many devices can generate large levels of noise power. An amplifier will produce “290 × Gain” white noise at its output over the bandwidth it was designed for. Many other devices also can produce quite a bit of noise (we’re usually trying to reduce the noise). If you want a very high-power noise source, you can cascade amplifiers to greatly increase the noise power output.
It should be noted that when driving amplifiers, receivers, etc., from a wideband high-power noise source, care must be taken not to saturate the receiving test circuit. An output filter can be used to band-limit the output and keep the total integrated noise power to a level that will not saturate whatever is being driven from the noise source.
Once the noise source is obtained, its output can be accurately measured using the technique discussed in this article to provide a noise source that’s as accurate as the calibrated noise source used for reference.
Roy Monzello is a Systems Engineer at Smiths Interconnect.
References
- “Fundamentals of RF and Microwave Noise Figure Measurements,” Application Note, Keysight Technologies.
- “Noise Source Components,” Mercury Systems Tech Brief.