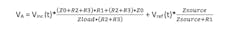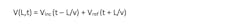Overcome Mismatched Load Impedance in Arbitrary Function Generators
Download this article in PDF format.
Arbitrary function generators (AFGs) are used to generate many different types of electrical waveforms, such as sine waves, square waves, triangular waves, and arbitrary waveforms. In addition, most electrical engineers use an AFG as a reference source for their device under test (DUT). With a relative frequency range from dc to 250 MHz, the latest AFGs can cover the audio frequency band, the video frequency band, and the radio frequency band. In all cases, impedance matching is required to maximize power transfer and minimize signal reflection.
The AFG’s output impedance should be equal to the load impedance or characteristic impedance. For example, in audio systems, 60 Ω is used as the characteristic impedance; in video systems, 75 Ω is used as the characteristic impedance. For the radio frequency band, the most common characteristic impedance is 50 Ω, which is the compromise value between minimum loss and optimum power-handling capability.
Most AFGs use 50 Ω as their characteristic impedance because of its wideband high-frequency capability and universality. Virtually all analog/RF parameters listed in product specification are measured under 50-Ω load-matching conditions.
But what happens if the load impedance is not 50 Ω? Will the actual output waveforms of a signal generator remain ideal under non-50-Ω load-impedance conditions? The answer depends on the degree of mismatch. Signal generators use a simple Thévenin equivalent circuit (Fig. 1) under dc or low-frequency or short-cable conditions.
1. An AFG’s output uses a simple Thévenin equivalent circuit.
According to Ohm’s law and Kirchhoff’s circuit laws, we could get:
We assume ZS is 50 Ω, and VS is 2 V p-p amplitude:
• When ZL is equal to 50 Ω, the VL should be 1 V p-p, half of the VS amplitude.
• When ZL is 1 MΩ or infinite resistance, the VL will be 2 V p-p, the same as the VS amplitude.
As this illustrates, the actual output waveform’s amplitude changes based on different load impedance under low-frequency conditions. But as frequency increases, the system circuit models become more complex. In this case, it may be necessary to regard the cable as a transmission line and consider reflection and complex load (not only resistance, but also inductance or/and capacitance).
Under certain mismatching conditions, the amplitude and shape of a waveform produced by an AFG can end up being significantly different from the ideal source output. These conditions are usually caused by mismatched load impedance or the use of mismatched long cables. The impact of bad reference waveforms can be significant, including measurement errors that lead to inaccurate conclusions and, under extreme conditions, damage to the DUT.
Displaying the Actual Waveform
The typical method for identifying the actual signal waveform is to use an oscilloscope to probe the load of the AFG or the input of DUT. This method requires an additional instrument and cable, adding time and increasing complexity. There must be a better way.
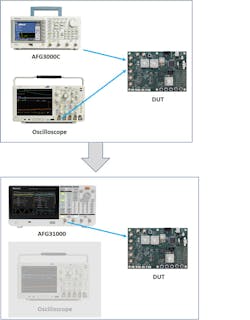
One of the development goals for our next-generation arbitrary function generator was to discover a way to display the actual waveform at the DUT, instead of just the nominal waveform as set on the AFG. This effort led to the inclusion of what we’re calling InstaView (short for instantaneous view) in our recently introduced AFG31000 arbitrary function generator.
With this function—for which we’ve received patents—all that’s needed is the cable between the AFG output and the DUT, which is already in place (Fig. 2). The user merely needs to enter cable parameters to show waveform changes in real time, along with the settings like frequency, amplitude, and waveform shape changes or impedance changes at the DUT.
2. Compared to previous-generation AFGs such as the Tektronix AFG3000C, InstaView simplifies test setup. All that’s needed is the cable between the AFG output and the DUT, which is already in place.
Equivalent System Models
To understand how this all works, we need to look at what’s involved in building equivalent system models and the underlying mathematical calculations.
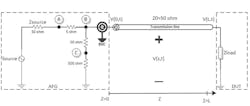
Figure 3 depicts an equivalent system model. The AFG circuits are simplified as an ideal voltage source with series 50-Ω source resistors. These three resistors compose a unidirectional bridge. We acquire sampling data through it and after arithmetic calculation, we can obtain the actual load waveform.
3. This is a depiction of an equivalent system model.
The transmission line is represented by the symbol of the coaxial cable with length L, which should have a 50-Ω characteristic impedance. The DUT has a load impedance, Zload, which could be pure resistance, inductance, or capacitance, or a combination of them. The arrow represents the incident waveform propagation direction. The reflection waveform propagates in the reverse direction.
Now let’s walk through a step-by-step analysis of this system.
1. DC or low-frequency range
The transmission line consists of two conductors: one is regarded as the signal path; the other is used as the return path. PCB traces on multilayer boards, such as the microstrip and stripline, can be transmission lines. Coaxial cables can be transmission lines as well. But whether the traces and cables actually end up being regarded as transmission lines depends on the maximum signal frequency or the fastest rise/fall time in relation to the cable’s physical length.
In the two equations below, L represents cable length, λ represents wavelength, v represents propagation velocity, fmax represent maximum frequency, TD represents transmission delay, and τr represents rise time.
When the cable length (L) is smaller than 10 times of wavelength (λ), or the waveform’s rise time (τr) is larger than 10 times of transmission delay (TD), the transmission-line effect can be ignored. That means we can regard the cable as ideal or lossless line with no attenuation and no phase delay.
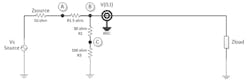
To simplify equations, we can use light speed, c, to replace propagation velocity v when we do calculations by hand. Figure 4 shows a simplified equivalent model diagram where the transmission line is replaced by an ideal line.
4. This is a simplified diagram under a low-frequency condition.
Based on Kirchhoff’s laws:
Zload is the load impedance and unknown value. Vs is the amplitude of the source. We can regard it as unknown value. VA, VB and VC are test points.
When Zload = 50 Ω:
There’s no reflection signal, so the B point waveform is same as the load’s and can be considered as the initial incident waveform.
2. High-frequency range with lossless transmission line
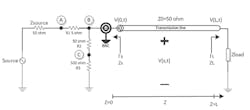
As frequency increases, the transmission-line effect is brought into play. But when the cable length is not very long and frequency isn’t very high, the transmission line’s attenuation elements R (distributed resistance) and G (distributed conductance) are small and can be neglected. Under these conditions, we can consider the coaxial cable as a lossless transmission line. The signal’s amplitude on a lossless transmission line will stay constant; only propagation delay occurs. Figure 5 shows the system models with a lossless transmission line.
5. Here’s the system model with lossless transmission line.
The reflection occurs when an impedance mismatch happens. The reflection coefficient, Γ, is defined as:
From this we can get the source reflection coefficient and load reflection coefficient:
When Zload ≠ 50 Ω, the ΓL will not be zero, which means there’s a signal being reflected. The reflected signal will propagate along the reverse z-axis to reach source terminator ZS.
ΓS is equal to 0, meaning no reflection occurs when the signal reaches source terminator ZS.
Based on this, we can consider this system as one reflection case. Only load-mismatched impedance can cause reflection. The reflected signal will propagate to source ZS. No second reflection occurs because the value of ZS is 50 Ω. The voltage at any point along the transmission line can be considered the sum of the incident waveform and the reflection waveform.
where Vinc represents the incident waveform or forward-traveling waveform; Vref represents the reflection waveform or backward-traveling waveform; v represents the propagation velocity; and z represents the distance along cable.
At point B:
At point A:
At point C:
We can determine the Vinc (t) and Vref (t) based on the previous equations. The load waveform V(L,t) is the composite of the delayed propagation Vinc (t) waveform and the advancing propagation Vref (t) waveform. The delayed or advancing phase value is calculated by L/v, or measured, before the calculation of load waveform. So, at the load:
Figure 6 provides an example of how we process and calculate waveforms based on the above principles and equations. After capturing waveform data on any two points, we calculate the actual incident waveform and reflection waveform. Finally, we obtain the actual load waveform based on the load equation above and present it to the user on the instrument’s display.
6. This process is used to capture load waveforms.
How Does It Work?
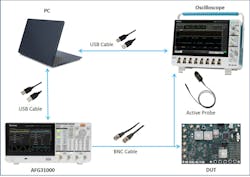
To determine the effectiveness of this approach, we conducted a series of tests using the setup shown in Figure 7 to compare calculated waveform data with actual data measured by an oscilloscope. The demo board we used supports many different types of loads (matching, non-matching). The PC pulls acquired data from the oscilloscope and calculates data from the AFG. It then compares the data to determine error. For dc or low ac frequency, we replaced the oscilloscope with a digital multimeter (DMM) for better measurement accuracy.
7. Calculated waveform data is compared against actual data measured by an oscilloscope.
In Figures 8 and 9, the X-axis represents the setting in Vdc and Vpp. The orange curves are voltages measured by an AFG and the gray curves are the voltages measured by a digital multimeter. As you can see, there’s overall extremely close alignment at these low frequencies.
8. This chart shows dc amplitude accuracy when measured by a DMM (50-Ω terminator + 90-cm BNC RG-58 cable) compared to InstaView.
9. Here, 1-kHz ac amplitude accuracy, measured by a DMM (50-Ω terminator + 90-cm BNC RG-58 cable), is compared to InstaView.
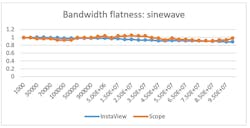
In Figures 10-13, the orange curves represent voltages measured by InstaView and the blue curves are the voltages measured by an oscilloscope. Figure 10 provides an analysis of flatness error with analog bandwidth. Figure 11 shows overall tight alignment when there’s a 50-Ω match condition. More indicative are Figures 12 and 13, which provide a waveform comparison under 1-MΩ mismatch and complex mismatch conditions, respectively. While some variances occur, they are slight and unlikely to result in significant measurement errors.
10. This comparison indicates the degree of flatness error within analog bandwidth between a scope measurement and InstaView.
11. As expected, there was strong alignment between InstaView and scope measurements for square waveforms under a 50-Ω match condition.
12. Here, InstaView has largely compensated for a 1-MΩ mismatch condition.
13. InstaView is able to adjust waveforms to match the desired output even under complex mismatch condition (combination of R, L, and C).
Applications
A single cable approach such as that described here offers a quick and convenient way to determine whether actual reference waveforms are what’s needed, and whether the load impedance or input impedance of the DUT matches and to what degree. In addition to saving time in test setup, InstaView can also serve as a good diagnostic tool for researchers or designers in the lab.
For example, if there are questions about the input reference waveforms or the input impedance of the DUT, all it takes is a simple button push to see the result on the display. This function also can serve as a good demonstration in educational settings, providing students with visual feedback on how waveforms react under matching and mismatching conditions.
Haiping Iv is a Senior Hardware Engineer at Tektronix Inc.
