Improve Scope SNR via Processing Gain
This file type includes high-resolution graphics and schematics when applicable.
Pulsed signal measurements with an oscilloscope can become challenging when there is a lack of sufficient dynamic range and signal-to-noise ratio (SNR). In many applications, whether commercial or military, low-level pulses are often difficult to detect and measure in the presence of much larger pulses. However, using a technique to “span down” the initial 3-dB bandwidth of an oscilloscope by means of digital downconversion can greatly enhance an oscilloscope’s SNR. In fact, it’s possible to view two pulses separated by 50 dB in amplitude on an oscilloscope with the proper enhancements.
The help comes in the form of vector-signal-analysis (VSA) software, which processes captured data from an oscilloscope and performs digital downconversion to show low-level pulses on a log-magnitude scale—even in the presence of much larger signals. The approach helps accelerate system-validation measurements on pulsed RF signals in aerospace and defense systems, as well as in commercial and industrial radar systems. The process can markedly improve measurement accuracy when evaluating the spectral, pulse envelope, frequency chirp, and phase-shift characteristics of an RF pulse train.
Teaming VSA software with a digital oscilloscope significantly extends the SNR of the oscilloscope. Such software has the capability to shift captured oscilloscope RF signal samples down to baseband in-phase and quadrature (I and Q) signal components, and then apply bandpass filtering and resample the signal data at a lower sample rate to greatly reduce the noise levels. The result is a higher dynamic range and lower SNR, allowing detection of low-level signals even in the presence of higher-level signals.
Software in Action
To demonstrate the effectiveness of this approach, a wideband 8-GHz oscilloscope was used to capture a pulse train with a large pulse, followed by a lower-level pulse that is 50 dB less in amplitude. The smaller pulse is 100,000 times lower in power than the larger pulse and ≈316 times smaller in voltage (100,000)0.5.
This two-pulse sequence repeats as part of the pulse train, with the lower-level pulse difficult to detect. The larger pulse has a power level of +6 dBm (about 1.4 mW), which results in a peak voltage of about 633 mV into a 50-⦠load. This is a –4-dBV peak level, or 20log(0.633). It also corresponds to a 1266-mV peak-to-peak signal into 50 â¦. In comparison, the smaller pulse—316 times smaller in voltage—is only 4 mV p-p (–44 dBm, –54 dBV peak level).
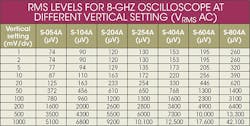
For this two-pulse example, the VSA software, which also works to control the oscilloscope front-end sensitivity, is set to +6 dBm (633 mV peak). This corresponds to a vertical measurement range of 1,266 mV on the oscilloscope. The oscilloscope has eight vertical divisions, so the setting is approximately 160 mV/div. Using the oscilloscope’s full 8-GHz bandwidth at this approximate 160-mV/div setting, the broadband root-mean-square (RMS) noise is around 5 mV, interpolated from a noise chart on the oscilloscope’s datasheet (see table).
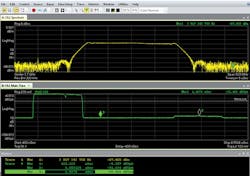
That translates to 15-mV p-p noise. As a result, the smaller pulse (at only 4 mV p-p) will be masked by the instrument noise in the measurement (15 mV p-p). In turn, it will not be discerned when using the full 8-GHz measurement bandwidth of the oscilloscope, with a linear scale and no averaging (Fig. 1).
Digital Downconversion
Although basic pulsed RF measurements can be made natively on a high-bandwidth oscilloscope, and there are certainly times that measurements on directly sampled signals are desired, external signal processing and analysis on captured signals can provide additional insights into measurement data. For example, a process called digital downconversion makes it possible to perform a wide range of RF pulse measurements with higher accuracy than native oscilloscope measurements, thanks primarily to the presence of lower noise due to an effect called processing gain.
Figure 2 shows the basic process of digital downconversion. By means of digital signal processing (DSP), measurement samples from the oscilloscope are multiplied by the sine and cosine of an imaginary oscillator with center frequency fc. This DSP technique is, in effect, “tuning” to the frequency of the input signal. The process converts the time samples into real and imaginary number pairs that completely describe the behavior of the input signal.
To reduce noise, these samples can be lowpass-filtered and then resampled at a lower rate to reduce the size of the data set, allowing fast-Fourier-transform (FFT) processing of the data at a later stage. The resulting digitally downconverted samples can then be placed into memory for further processing, such as calculating the FFT.
Important demodulation information comes from this digital-downconversion process. First, when the digital local-oscillator (LO) fc is equal to the carrier frequency of a modulated signal, then the output of the digital filters, which includes the real or in-phase signal component, I(t), and the imaginary or quadrature part, Q(t), consists of time-domain waveforms that represent the modulation on the carrier signal.
More specifically, a mathematical representation of the captured input signal is:
A(t){cos[2πfct + θ(t)]}
where the amplitude modulation, A(t), can be written as:
A(t) ≈ [I(real2 + Q(imaginary)2]0.5
and the phase modulation, θ(t), can be written as:
θ(t) = tan-1[Q(imaginary)/I(real)]
Displaying the I and Q results in terms of magnitude coordinates yields a view of the amplitude modulation, and showing the I and Q results in terms of phase coordinates yields a view of the phase modulation. By taking the derivative of phase modulation, frequency modulation (FM) is:
FM = dθ/dt
By adjusting the width of the lowpass filters, it is possible to set a defined span around the center frequency. Here, the filter width is wide enough to pass a signal of interest, but narrow enough to filter out much of the noise surrounding the signal of interest.
If the oscilloscope’s captured data is imported to a PC running the VSA software, it can be digitally downconverted into I and Q baseband data, bandpass-filtered, and then resampled. This process can greatly decrease the amount of noise in the measurement data. Essentially, the process “tunes” to the center frequency of the signal and “zooms” into the signal to analyze its modulation, providing “processing gain” for the captured data.
Taking on Two Pulses
For the two-pulse example, the oscilloscope’s original 8-GHz-wide measurement and its associated noise are reduced to a 500-MHz-wide measurement. It is centered on the 3.7-GHz carrier with an instantaneous measurement bandwidth slightly wider than the width of the signal modulation.
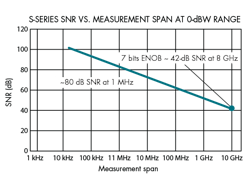
The reduction in measurement bandwidth corresponds to a SNR improvement of 10log(oscilloscope bandwidth/span) = 10log[(8 × 109)/(500 × 106)] = 12 dB. The enhanced SNR, combined with the ability of the VSA software to show a log magnitude scale and the use of averaging, makes it possible to display the smaller pulse in the presence of the larger pulse (Fig. 3). Fig. 4 graphically depicts the improvement in SNR by narrowing the span.
A similar plot can be drawn to show the improvement in dynamic range that’s possible when measuring narrowband signals (Fig. 5). The boost in dynamic range of 10log(oscilloscope bandwidth/span) when measuring narrowband signals in an FFT view does not fully describe the spurious-free dynamic range (SFDR) or harmonic distortion characteristics of the oscilloscope. However, it does give an idea of where the noise floor will lie in an FFT measurement. As the resolution bandwidth is decreased, the total noise is divided among smaller increments of time, resulting in the noise floor dropping. The plot of Fig. 5 does not account for limitations due to various spurious responses; therefore, the SFDR as shown remains limited to around 50 dB.
Brad Frieden is Applications Engineer for Aerospace Defense Industry Solutions at Keysight Technologies.