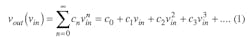Reviewing The Basics Of Intermodulation Distortion
This file type includes high resolution graphics and schematics when applicable.
Intermodulation distortion (IMD) can wreak havoc in modern wireless-communications systems. The better it is understood, the better its effects can be minimized. IMD can be described by examining the linearity of a two-port network. This study of IMD will explore the relationship between the intercept points and the coefficients of the polynomial that is used to model the transfer function of an amplifier.
Increasingly crowded spectrum brings with it greater possibility of interference. As a result, system designers are striving to reduce interference susceptibility, for example, through improved linearity. A system's linearity governs how much IMD will occur within it, which in turn can create interference. Through improved linearity of the system building blocks, the overall susceptibility of a system to interference can be decreased.
IMD occurs as two or more signals pass through a two-port network with a nonlinear transfer function. The spectrum at the output of the device is comprised of the original signals and additional spurious signals. The additional spurious signals can cause interference within the original system or in other systems. When the spurious signals are of sufficient amplitude, they can overpower the signal of interest, resulting in interference and, in extreme cases, loss of transmitted information, such as voice, data, or video. The undesirable effects of IMD can be mitigated, by improving the linearity of system components (amplifiers, other semiconductors, and even passive elements), which cause IMD.
To understand IMD, consider a two-port network, such as an amplifier, with the nonlinear transfer function as shown in Fig. 1:
where:
c0 = the DC offset;
c1 = the voltage gain; and
{c2,c3,...cn} = the nonlinear distortion coefficients.
This article will focus on linear, second-order and third-order terms, although the analysis is similar for higher-order terms.
Let a test signal, vin, be the superposition of two sinusoids of unequal frequency, that is:
where s1(t) and s2(t) are signals in a different system, or they may originate from other sources within the same system. This analysis assumes un-modulated test tones for simplicity, although the same processes occur when modulated signals pass through nonlinear circuitry.
If the test signal s(t) is applied to the nonlinear two-port network, the result is:
Using the trigonometric identity,
The second-order term can be expanded as:
Notice that the output consists of frequency components that were not present in the input. The second-order term in the power series produces harmonic distortion of both input sinusoids. It also produces mixing terms. Note that the mixing terms simply represent upconversion and downconversion processes. Additionally, a DC offset is produced. The down-conversion term can pose problems in heterodyne receivers because it can interfere with the desired signal at the intermediate frequency (IF). In a transmitter, the mixing terms and the harmonic distortion terms can be problematic in that they may cause it to transmit energy within other portions of the spectrum, blocking or interfering with desired signals at those other frequencies. DC terms can cause problems in homodyne receivers by saturating the DC-coupled baseband amplifiers.
The same trigonometric identity can be used to expand the third-order terms yielding:
Like the second-order term, the third-order term produces spurious signals in the output that were not present in the input. The third-order term produces scaled copies of the original signal (amplitude distortion), harmonic distortion, and mixing terms. The difference mixing terms form new signals that are spectrally close to the original signals, making them difficult to remove with filters. In fact, they may fall within the passband of the system and cause interference. Here again, the sum mixing terms and the harmonic distortion terms may cause a transmitter to transmit in adjacent bands inadvertently. The amplitude distortion is unacceptable in systems that use higher-order modulation schemes such as 16-state quadrature amplitude modulation (16QAM), because the distortion results in an error component in the received vector, degrading the receiver's bit-error rate (BER). A spectral plot of the output that might be seen on a spectrum analyzer is shown in Fig. 2.
In order to further simplify the analysis, it is customary (though not necessary) to make the amplitude of the input sinusoids equivalent, that is a1 = a2 = a. The coefficients of the linear, second-order IMD, and third-order IMD terms become:
respectively.
Continued on page 2
Page Title
As a increases, the linear term increases as a1. The second-order IMD term
increases as a2 and the third-order term increases as a3. When these coefficients are plotted as a function of a, on a log-log plane, the exponent simply becomes the slope of each of the three lines, as shown in Fig. 3. Note that the nth-order term increases at a rate n times that of the linear term.
In reality, an amplifier's output doesn't increase without bound as Fig. 3 suggests. Rather, the amplifier's output can be limited by, among other factors, its power supply rails. The finite power supply can force the transfer function to limit or compress as the input amplitude increases (Fig. 4). This compression, modeled by the higher-order terms in the power series, arises as a result of higher-order terms becoming a significant portion of the output.
It is common to identify the point where the actual output deviates from the ideal output by 1 dB. This point is known as the 1-dB compression point, represented as P1dB.
For convenience, a line 1 dB below the ideal output is shown in Fig. 4.
Parameter P1dB can be estimated when the third order term dominates. Such is the case in differential amplifiers where the transfer function exhibits odd-symmetry. It is simple to find the input amplitude where the distorted output is 1 dB less than the ideal, undistorted output:
The intersections of the second-order and third-order lines with the line produced by the linear term are known as the intercept points (IP). The second-order intercept point is called IP2 and the third-order intercept point is called IP3. The intercept points are further defined with respect to the input amplitude or the output amplitude where the intersections occur. For example, the input IP3 is represented as IIP3, whereas the output IP3 is represented as OIP3.
The intercept points are defined as if the linear term and higher-order terms increased without bound. They provide a means of quantifying the linearity of a two-port, and as a result, facilitate comparison with other two-ports. The concept of the IP is a powerful and versatile tool and is used very frequently. The coefficients {c2, c3, …, cn} have the effect of shifting their respective lines up or down (in a log-log plane). As c2 and c3 approach zero, their lines shift down, intuitively causing their respective intercept points to increase.
As was mentioned above, the intercept points occur where the coefficients of the IMD terms are at parity with the coefficient of the linear term. Thus, if the linear coefficient is equated with the second order IMD term, and solving for a, IIP2 can be found with Eq. 14:
Similarly, IIP3 can be found with Eq. 15:
In practice, c2 and c3 are unknown. Moreover, they are difficult to measure directly. Fortunately, another method can be used to measure IP2 and IP3.
As was seen earlier, the slopes of the linear, second-order, and third-order lines are m1 = 1, m2 = 2 and m3 = 3, respectively. Referring to Fig. 5, equations that describe the two lines can be written as:
The lines intersect according to the conditions of Eq. 18:
Solving the system of equations for Pout and noting that mn = n, results in Eq. 19:
It is possible to use a spectrum analyzer, in conjunction with Eq. 19, to measure OIP2 and OIP3. For a given Pin1, the output amplitude of the fundamental (Pout1) and the IMD term (Poutn) are measured. Simple substitution of the measured values into Eq. 19 yields OIPn. This measurement is routinely performed and should be made such that the amplifier's fundamental output is not strongly influenced by the higher-order terms. That is, it should be made while the input amplitude is well below P1dB. Otherwise, Pout will contain an error component.
To point out one final interesting relationship, refer to Eqs. 13 and 15. It can be seen that IIP3 and P1dB are related to one another as:
or in decibels as:
This is true, of course, as long as the second-order term is insignificant. In practice, this relationship is commonly observed for a wide variety of amplifier topologies.
In summary, the concepts of linearity and intercept points were reviewed, and it was shown that a spectrum analyzer could be used to measure intercept points. Problems caused by linearity can arise in all parts of a system. By measuring, analyzing, understanding, and optimizing a system's linearity, it is possible to dramatically improve its performance. By understanding the types of problems that nonlinearities can create, and how to overcome them, the designer is better equipped to achieve success.
For further reading
Behzad Razavi, Design of Analog CMOS Integrated Circuits, McGraw Hill, 2001.
David M. Pozar, Microwave Engineering, Addison Wesley, 1990.
Jarek Lucek and Robbin Damen, "LNA Design for CDMA Front End," RF Design, February, 1999.
Ken Kundert, "Accurate and Rapid Measurement of IP2 and IP3," www.designersguide.org.