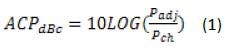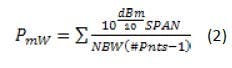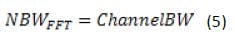Understanding Adjacent Channel Power Measurements In Spectrum Analysis
This article will review adjacent-channel-power (ACP) measurements. ACP is a measure of the nonlinear characteristics of a device under test (DUT) and indicates the amount of spectral regrowth occurring in adjacent channels. This article will explain how the measurement is performed and how to optimize the measurement for speed, repeatability, and dynamic range. This article will also explore new techniques for making this measurement with the fastest and most repeatable results.
ACP History
ACP measurements have been performed for many years. Originally, ACP measurements were used for narrowband analog modulated signals and measured the ratio of the upper and lower channels to the total power transmitted. The total power transmitted was defined as the carrier plus the majority of power in the upper and lower channels. Today, an ACP measurement is defined as the ratio of one or more upper and lower intervals of power to the total carrier power across the bandwidth of the channel.
Cellular communications systems have relied on ACP measurements to ensure that power radiated into an adjacent channel is limited—to ensure that the signal-to-noise ratio (SNR) in the adjacent channel does not interfere with communications in that channel. Cellular standards such a W-CDMA, cdma2000, and LTE all have defined methods and limits for ACP measurements. These standards go even further and even provide more descriptive names for ACP measurements. For example, cdma2000 adopted Adjacent Channel Power Ratio (ACPR) and W-CDMA adopted Adjacent Channel Leakage Ratio (ACLR) as more specific names for their versions of ACP measurements. GSM and EDGE have similar requirements that use what are called Output RF Spectrum (ORFS) measurements to ensure that power radiated into adjacent channels does not exceed certain levels. Most modern spectrum analyzers have programmed, predefined settings for various standards that allow for quick measurement setups.
Download this article in .PDF format
The ACP result can simply be stated as Eq. 1:For narrowband analog modulated signals, the phase noise present in the local oscillator (LO) accounted for most of the power present in the adjacent channels in these systems. Today, with the introduction of wide-bandwidth signals, the power in the adjacent channel(s) can potentially be from a combination of several factors, including phase noise, intermodulation distortion (IMD), and the noise floor of the system. Similarly, these factors influence the dynamic range a spectrum analyzer can achieve in making an ACP measurement.
where is the power in the adjacent channel and is the power in the channel.
Figure 1 is the screen image of an Agilent N9020A MXA signal analyzer performing an ACLR measurement of a W-CDMA signal. The ACLR measurement is defined as the relative power in the adjacent and alternate channels to the amount of power in the carrier measured in a 3.84-MHz bandwidth. The spacings of the adjacent and alternate channels to the carrier are 5 and 10 MHz, respectively. The power levels in the channels are calculated using the integrated power method as shown in Eq. 2, where the power level of each trace point (in logarithmic dBm) in the channels is converted to a linear milliwatt (mW) value and the values are summed together with the appropriate integration parameters as shown in Eq. 2:
Compensation in power is then applied to account for the root-raised cosine filtering used in W-CDMA.
1. W-CDMA ACLR measurement of the adjacent and alternate channels for a 25-MHz span at a center frequency of 1 GHz.
Dynamic Range
The spectral regrowth in wide-bandwidth signals in adjacent and alternate channels is primarily composed of coherent and noncoherent distortion products. Coherent products are normally comprised of third- and fifth-order nonlinear distortion products that develop within the DUT. Noncoherent products are noiselike in nature and come from phase noise associated with the system’s LO and/or the noise floor of the DUT.
A spectrum analyzer is not immune to spectral regrowth. The amount of distortion produced , however, can be greatly affected by the settings of the instrument. The third- and fifth-order distortion products that are internally generated in the spectrum analyzer are a function of the analyzer’s mixer level, where the mixer level can be calculated using Eq. 3:
Increasing the internal or external attenuation will decrease the internally generated spectrum analyzer coherent distortion products by reducing the level present in the mixer. Increasing attenuation has an adverse effect on the spectrum analyzer, however, by increasing its noise floor. This is why it is challenging to optimize spectrum analyzer dynamic range in ACP measurements.
Dynamic Range Optimization
Before attempting to choose optimum spectrum analyzer setting for dynamic range, it is first necessary to understand the dynamics associated with the various distortion products involved in the measurement. Third-order distortion products will appear primarily in the adjacent channel whereas fifth-order distortion products dominate in the alternate channels. As the mixer level is reduced by increasing attenuation, fifth-order distortion products will drop at a much faster rate than third-order distortion products (5:1 versus 3:1). This will cause the coherent distortion products to quickly fall to levels at or below the noise floor of the spectrum analyzer in the alternate channel , while the third-order distortion products will still be above the noise floor in the adjacent channel. Increasing attenuation will now negatively affect the ACP performance in the alternate channel, increasing the noise floor.
The best method to deal with the tradeoff between reducing the coherent distortion in the adjacent channel while not compromising the dynamic range in the alternate channel is to use noise corrections or noise floor extensions. First, increase the attenuation to reduce the internally generated distortion products in the adjacent channel to a point that ACP results do not change as attenuation is increased. At this attenuation level, there is an assurance that the DUT’s ACP performance in the adjacent channel is what is being measured. Noise corrections or noise floor extensions can then be used to reduce the noncoherent noise that will be present in the alternate channel that comes from the noise floor of the spectrum analyzer.
If phase noise is the limiting factor, most modern spectrum analyzers allow a user to optimize phase noise offset either close in or far from the carrier when measuring standards such as Tetra, where phase noise dominates the measurement.
Measurement Uncertainty
As in most nonlinear distortion measurements, such as measurements of harmonics, third-order intercept (TOI), and second harmonic inversion (SHI), care must be taken that internally generated intermodulation products do not cancel the distortion products from the DUT. This can occur when internally generated distortion products are close to the same amplitude as the DUT distortion products but 180 deg. out of phase. When large improvements can be observed to ACP results with slight changes to the input attenuation or input level, this is the most likely cause. When the amplitudes of the DUT and internally generated distortion products are equal, the uncertainty in the measurement ranges from +6 dB to –infinity. The smallest uncertainty in measurement results can be maintained when spectrum analyzer distortion products are several dB below the DUT distortion products. This may require using a higher-performance spectrum analyzer in some cases to eliminate these uncertainties.
Speed Versus RepeatabilityThe Agilent X-Series signal analyzers have a built in Adjust for Minimum Clip feature that can be used to automatically set the mixer level based upon the input signal level. The mixer level is optimized to provide the optimum dynamic range without excessive measurement uncertainty.
Most modern spectrum analyzers use an average or root-mean-square (RMS) detector for measuring the power in the channels when performing a swept-tuned ACP measurement. The variance observed will be given as Eq. 4:
In most cases, the channel bandwidth, resolution bandwidth (RBW), and span are fixed based upon the ACP standard being measured. Sweep time will need to be increased if more repeatable results are needed.This will have an adverse effect on the overall measurement time.
Agilent Fast Power Option
The Agilent X-Series signal analyzers have a Fast Power option that allows a user to rapidly perform power measurements such as channel power, adjacent channel power, occupied bandwidth, and X-dB measurements (Option FP2). First, the power measurements are accelerated in hardware by performing real-time overlapped Fast-Fourier-Transform (FFT) computations in field-programmable-gate-array (FPGA) code. The results of each FFT are RMS averaged together to provide the real-time spectrum in which the power results are computed. This is a SCPI-only feature that allows users to perform measurements such as ACP directly within the hardware. As an example, a W-CDMA ACLR result can be requested by means of programming while in EVM measurement mode. For such a measurement, a total measurement time of 3 ms can be achieved with an acquisition time of 1 ms.
The Fast Power method improves repeatability because all the channels are measured simultaneously in a much wider bandwidth. As an example, the repeatability of the swept ACLR measurement in Fig. 1 can be calculated. The measurement setup uses a sweep time of 3 ms, an RBW of 100 kHz, and a channel bandwidth of 3.84 MHz in a span of 25 MHz. This swept measurement requires an overall time of 13 ms for completion. The repeatability of the swept measurement can be calculated by using Eq. 4:
It is now possible to compare the repeatability and measurement time of the Fast Power method using a 1-ms acquisition time and total measurement time of 3 ms to the swept example. For the Fast Power method, the following relation can be used for noise bandwidth (NBW):
Therefore, the Fast Power repeatability is:
In summary, a Fast Power ACLR measurement can be made four times faster and with repeatability improved by nine times over a swept measurement.
Figure 2 depicts various repeatability values for acquisition times for swept-tuned ACP and Fast Power ACP measurements. The blue and red lines are the theoretical results for swept-tuned ACP and Fast Power ACP measurements, respectively, from Eq. 4.
Swept tuned measurements will always provide higher dynamic range because a narrow bandwidth analog intermediate-frequency (IF) filter will be used. This narrow IF bandwidth filter provides a much lower peak power that will be observed at the analyzer’s analog-to-digital converter (ADC) compared to when the entire bandwidth is measured at once, as in the Fast Power case. If dynamic range is a major requirement, a swept-tuned ACP measurement should be used. If measurement speed and repeatability are needed in an automated test environment where maximum dynamic range is not the dominating factor, the Agilent X-Series signal analyzer’s Fast Power option is far superior to other methods.
Summary
This article has covered a broad set of issue related to making ACP measurements. As modulation standards evolve, other measurements, such as the spectral emission mask (SEM) measurements, will allow users to gain more insight into the linearity of their DUT. Measurements made in conjunction with linear distortion measurements, such as error vector magnitude (EVM) measurements, will ensure that the end users of this equipment enjoy better communications and a clean use of the limited spectrum.