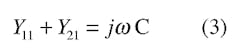Model MMIC Nichrome Resistors
Nichrome resistors are commonly used as part of the process of fabricating monolithic microwave integrated circuits (MMICs). An effective MMIC model, however, must include an accurate model of a nichrome (NiCr) resistor. Fortunately, what follows is a methodology for the data-based parameter extraction required for developing an accurate NiCr resistor model. These resistors have been fabricated on gallium-arsenide (GaAs) semi-insulating substrates, and then are diced and bonded onto a coplanar-wave-guide (CPW) test fixture so that two-port scattering (S) parameters can be measured over a wide band of frequencies. An algorithm based on the de-embedded S-parameters has been developed to extract the electrical parameters of an equivalent circuit for the NiCr resistor. The frequency-dependent model parameters have been extracted to 15 GHz for a large number of resistors of varying geometries and curve-fitted equations for the model parameters have been obtained. As will be shown, the model-predicted S-parameters agree closely with the measured results.
MMICs consist of planar integrated active and passive elements that determine the circuit operation. Passive elements are composed of lumped elements such as resistors, capacitors, and inductors and distributed elements such as transmission lines. In MMIC technology, the resistors are extensively used in feedback circuits, bias circuits, and as terminations. Two types of resistors are commonly used in MMIC fabrication, namely, thin films of lossy metals and lightly doped GaAs active layer (mesa resistors).1 Metal thin-film resistors are more temperature stable and are used as precision resistors of low to moderate values. These are usually fabricated from TaN and NiCr although other metals may be used.1,2 NiCr resistors have low thermal coefficient of resistance (TCR), small parasitic values, and are widely used in a variety of circuit designs 3,4
The resistors in this research were grown in-house by means of RF sputtering. NiCr resistors have been grown on 200-µm semi-insulating GaAs substrates with 1.0-µm-thick polymide used as the passivating layer. The sheet resistance is typically about 40 Ω/square and the TCR is about 250 × 10−6/°C. The resistor values selected for this work range from 5 Ω to 2 kΩ.
Figure 1 shows a top view of a typical NiCr resistor with input and output pads. For RF characterization of the diced resistors, the authors designed a CPW test card with 50-Ω input and output lines (Fig. 2). The resistor chip is die bonded onto the ground plane of the card and the resistor terminals are wire bonded to the input/output (I/O) signal lines by means of 1-mil-diameter gold bond wires. The bonded chips are then characterized for small-signal S-parameters to 15 GHz using ground-signal-ground (G-S-G) wafer probes from Cascade Microtech (Beaverton, OR) and an 8510C microwave vector network analyzer (VNA) from Agilent Technologies (Santa Rosa, CA) in conjunction with the Cascade Microtech probe station.
The two-port S-parameters of the bonded resistor chips were measured at the CPW Test Card I/O planes 1 −1 and 2 −2 as shown in Fig. 2. Multiple-step de-embedding was carried out to extract the S-parameters at the resistor places 1´ −1´ and 2´ −2´ by using software from Agilent-EEsof (Santa Rosa, CA). Bond-wire and bond-pad models used in this analysis are given below.
The inductance of the bond wire can be calculated from the following expression:5
where:
d = the diameter of the gold wire and
l = the length.
For 1-mil-diameter bond wire, the value of LBW comes out to be 0.7 nH/mm. The bond-pad capacitance can be obtained from the GEC-Marconi foundry model6 using the expression:
where:
W = the dimension of the square bond pad (in µm)
The bond pad used for this study measures 10 × 100 µm and the corresponding value of CBP is 0.028 pF.
Figure 3 shows the electrical lumped-element equivalent-circuit model for the NiCr resistor. In this model, R represents the RF resistance of the device under test (DUT), L is the series inductance, which is due to the finite length of the transmission-line length associated with the resistor, and C is the shunt capacitance which accounts for the RF fringing fields to the ground plane. This model assumes a symmetrical fringing capacitance due to the symmetry of the resistor structure. For the two-port circuit in Fig. 3, the Y-parameters are related to the element values by:
Page Title
The de-embedded S-parameters at the resistor planes are transformed to a Y-matrix and, using Eqs. 4, 5a, and 5b the electrical parameters R, L, and C, are computed for various frequencies. The variations of the extracted model parameters with frequency for a few resistors are shown in Figs. 4 and 5. Figure 4 shows the values of R normalized to Rdc (DC/low frequency value of the resistor) as a function of frequency for three different values of NiCr resistors. It is apparent here that R increases with frequency and this may be due to skin effects. The authors have generated a data base for resistors of various geometries and from this experimental data, have created a geometry-scalable model for parameter R as a function of frequency:
where:
Rdc = the DC value of the resistor and is related to the physical parameters6 by the relationship:
where:
δl = 1.0 µm,
δW = 1.0 µm,
Rc = the contact resistance (25 Ω-square),
Rsq = the sheet resistance (40 Ω-square),
l = the length of the resistor (in µm),
W = the width of the resistor (in µm), and
f = the frequency (in GHz).
The expression given by Eq. 6 is valid within ±5 percent over the frequency range to 15 GHz. Figure 5(a) shows the values of the inductance (L) of the resistor (normalized to its value at 50 MHz) as a function of frequency for three values of the resistor length. The resistor width is 10 µm for all curves. It can be seen from Fig. 5(a) that L is an increasing function of frequency. Figure 5(b) shows the dependence of L at 50 MHz as a function of resistor length for a resistor width of W = 10 µm. From Figs. 5(a) and 5(b), it can be seen that L is a strong function of resistor length and frequency. Combining the data of Figs. 5(a) and 5(b), the authors have derived a curve-fitted empirical expression for the inductance L for a resistor width (W) of 10 µm:
where:
l = the resistor length (in µm),
f = the frequency (in GHz),
a0 = 0.011,
a1 = 1.0 × 10−4
b0 = 0.938,
b1 = 0.106,
b2 = 2.7 × 10−4,
b3 = 4.486 × 10-4, and
L(f) = the resistor inductance as a function of frequency (in nH).
Similar equations have been derived for different resistor widths. The authors have found that the fringing capacitance (C) is very low and weakly dependent on frequency. For practical purposes, it may be treated as a constant value of 20 fF.
Self Consistency
To check the self-consistency of the resistor model presented here, the authors computed the S-parameters of the resistor equivalent network with the element values as obtained from the model Eqs. 6 and 7 and compared these values with measured S-parameters. Figure 6(a) shows the modeled and the measured (and subsequently de-embedded) values of |S11| and |S21| at the device plane as a function of frequency for a NiCr resistor of length 30 µm and width of 10 µm (the DC value of the resistor is 135 Ω). Figure 6(b) shows the corresponding values for < S11 and < S21—both measured and modeled. From these results, it is clear that the parameters computed from the model agree reasonably well with the measured values.
This report has offered a methodology for the RF characterization and data-based RF modeling of NiCr resistors used extensively in MMICs. The technique for extracting the parameters of the lumped-element electrical equivalent-circuit parameters has been discussed in details and based on this, some curve-fitted polynomial equations valid within ±5 percent to 15 GHz have been obtained for CAD applications.
ACKNOWLEDGMENTS
The authors are thankful to the Director, Solid State Physics Laboratory, Delhi, for his kind permission to publish this work. We would like to thank Dr. (Mrs.) R. Gulati, Mr. B.K. Sehgal, and Mrs. Seema Vinayak for the supply of samples. Useful discussions with Dr. H.P. Vyas are also greatly acknowledged.
REFERENCES
- R. Goyal, Monolithic Microwave Integrated Circuits: Technology & Design, Artech House, Norwood, MA, pp. 342-346.
- R. Williams, Modern GaAs Processing Methods, second edition, Artech House, Norwood, MA, 1970, pp. 302-305.
- J. Zelenka, V. Chudoba, and J. Rehak, "Thin resistive film with temperature coefficient of resistance close to zero," Thin Solid Films, 200 (1991), pp. 239-246
- L.I. Maissel and R.Glang, Handbook of Thin Film Technology, McGraw-Hill, New York, 1970.
- Steven L. March, "Simple Equations Characterize Bond Wires," Microwaves & RF, November 1991, pp. 105-110.
- GEC-Marconi F20 Process guide manual, pp. 5-14