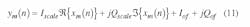Wireless applications using WiMAX high-date-rate technology are poised for growth in the next several years. Based on orthogonal-frequencydivision-multiplexing (OFDM) techniques, WiMAX holds the promise of broadband wireless access (BWA) as part of the "last mile" of multimedia services networks. Last month, this three-part article series on WiMAX testing opened with a review of the WiMAX physicallayer (PHY) and media-access-control (MAC) protocols as outlined in the IEEE 802.16-2004 standard, and the fundamental features of a baseband transceiver for WiMAX. In this second part, a baseband WiMAX receiver will be proposed, along with the key algorithms for its various measurement capabilities.
Last month, various elements of the WiMAX baseband receiver model were introduced, including the effects of inphase/quadrature (I/Q) gain imbalance (see Fig. 7 from Part 1, Microwaves & RF, July 2006, p. 76) and the effects of quadrature error (see Fig. 8 from Part 1, Microwaves & RF, July 2006, p. 76). In the baseband transmitter and channel model, the effects of I/Q origin offset and I/Q gain imbalance are introduced into time-domain signal as:
When Iscale = Qscale, the I/Q imbalance will be zero. When both Iof and Qof are zero, there is no I/Q offset. Figure 7 shows the effect of IQ gain imbalance in the constellation of the received symbols.
Quadrature skew error indicates the orthogonal error between the I and Q signals. Ideally, I and Q channels should be exactly orthogonal (90 degrees apart). When the orthogonality is not ideal (less or more than 90 deg. apart, or 90 ± , then a quadrature error can be observed. In the baseband signal model, the Q offset is introduced into the time-domain signal as:
where:
α = the quadratic error.
When α is equal 0 deg., ym(n) will be equal to xm(n) (no quadrature error). Figure 8 shows the effect of quadrature error in the constellation of the received symbols.
The received signal can be modeled (without the I/Q impairments) as:
where:
θm(k)carrier dep = the carrier-dependent phase rotation which is mainly caused by sample timing offset; and
Γm = the common gain offset which can be due to the variation of the gain of the amplifiers.
All the other noise sources are either folded into the AWGN term , zm(k), (if additive) or into the channel-frequency response, H(k), (if multiplicative).
Figure 9 shows a block diagram of the proposed WiMAX test receiver. The receiver is designed for test and measurement purposes, and there are some differences from the actual receiver algorithms that would be used in a WiMAX product. Note also that the receiver is a digital baseband receiver that processes the I/Q data that is provided by the analog front end of any receiver or vector signal analyzer. The received signal is also passed through the channel emulator to add the desired impairments (for test purposes) that are mentioned above. Therefore, the received signal represents I/Q samples that include the possible impairments due to the actual hardware (at the transmitter and receiver front-end) as well as the intentional impairments that are included in the channel emulator.
The transmitter can be any signal source that is transmitting standard WiMAX signals. It can be a vector signal generator (VSG) or a simulator. The authors have developed a standardsbased digital baseband transmitter in MATLAB software in order to test WiMAX performance in stand-alone mode. The simulated transmitter includes functions like channel coding, all possible modulation (BPSK, QPSK, 16QAM, 64QAM) and coding options (except turbo coding), all possible cyclic prefix options, uplink and downlink burst generation, all possible sampling rate and bandwidth options, flexible number of symbols within a burst, and ability to generate random and standard test data. However, as mentioned above, it is not necessary to use the transmitter simulator. The main goal is to test third-party transmitter products with the proposed receiver. However, it is desirable to have the option of using synthetic data from the simulated transmitter as well for debugging and cross-checking purposes. No matter which transmitter is used, as long as it is a IEEE 802.16-2004 standard based transmitter, the proposed receiver is designed to function properly, and all the blocks that are necessary to test and measure the transmitter quality are included as shown in Fig. 9.
Page Title
The baseband receiver, which is simulated in MATLAB, performs numerous operations: find the RF burst and packet edge (starting point) for the burst; estimate and correct the coarse frequency offset; estimate and perform coarse and fine symbol time synchronization; estimate packet (RF burst) end position, and extract useful packet information; perform fine frequency-offset estimation and correction of remaining frequency offset; remove CP and convert time-domain signal to frequency-domain symbols; estimate the channel-frequency response (CFR) and correct symbol rotations due to common and carrier dependent phase offset; employ frequencydomain equalization using the CFR; detect the symbols and obtain soft symbol values to be used by the channel decoder; employ de-interleaver/decoder/ derandomizer; decode the FCH field and check the CRC. In the following subsection, a brief explanation for each block will be provided. Note that some of the blocks are standard signal-processing blocks like De-interleaving/Decoder/ Derandomization, FFT, CP removal, etc. Since information about these blocks is widely available, they will not be explained further here.
Note that in WiMAX (like other wireless-communication systems), training sequences are inserted within the data symbols to help synchronization and channel estimation. The downlink subframe begins with two OFDM symbols used for synchronization and channel estimation at the subscriber station. These two symbols together represent the preamble of the DL subframe and are referred to as the "long preamble." The uplink subframe begins with one OFDM symbol that is used at the base station for synchronization to the individual SS. This single uplink symbol is referred to as the "short preamble." Figure 10 shows the long and short preamble structures. The first symbol in the long preamble is composed of every 4th OFDM carrier (50 out of 200 total). Therefore, the time-domain signal has four repeated parts. While the first symbol in the long preamble is useful for coarse signal acquisition, it is not sufficient for detailed channel measurement and correction. Therefore in the downlink subframes, the first symbol is followed by another of the same length, containing alternate active carriers. The second symbol in time domain has two repeated parts.
Packet detection is employed to see if there is a useful packet or not (and to find the starting point of that packet). The repeating structure of the training sequences is used in this search. Two sliding windows are used. The first window is used to calculate the autocorrelation between the received signal and a delayed version of it. The amount of the delay is equal to the length of the repeating sequence, depending on whether it is downlink or uplink. The second window is used to obtain the received signal power that is used to normalize the decision statistics, so that the decision variable does not depend on the instantaneous power. The size of both windows is same, M. The values of the first and second windows can be expressed as:
and the decision variable is:
where:
y(n) = the received signal,
and
M = the window size.
If the magnitude of d(n) exceeds a threshold, it can be assumed that there is an incoming packet starting at the point at which d(n) exceeds that threshold. The selection the threshold is a design criterion for which there is a trade-off between false alarm and miss rates.
The authors have introduced additional modification to the above method, including the use of different D in the downlink (D = 128) and uplink (D = 64), adaptive threshold (start with high threshold and gradually decrease it). In addition, for calculation of b(n), the authors realized that it is better to employ the following:
Figure 11 presents a sample output of the packet-detection algorithm. It shows the results after autocorrelation and moving average filtering. The output samples are tested against a threshold. Whenever a point is reached where the samples exceed the threshold, it is declared a packet, and that point is assumed as the starting point of the packet. Figure 11 was obtained for a good SNR value (SNR = 80 dB) where the correlation of the noise is close to zero, and the correlation of the repeated parts are close to one. For low SNR values, the peak will decrease. Note also that the correlator output around the peak is not like an impulse (or a narrow pulse), it is a fairly wide pulse. Therefore, the output of the packet detection provides only a rough idea about where the packet starts.
Frequency offset is estimated using the training sequences, such as the Moose method described in ref. 13. The average phase difference between two identical parts of the training sequences is calculated and then normalized to obtain the frequency offset. The average phase difference can be calculated as:
Page Title
The mean phase value is then used to calculate the frequency offset as:
In the downlink, for coarse frequencyoffset estimation, the two length-64 blocks are used in the middle of the first symbol (M = D = 64). There are two advantages to doing this:
- By using only shorter blocks of 64, larger frequency offsets can be compensated.
- Using middle blocks, the effect of inaccuracy for coarse timing on frequency-offset estimation can be reduced. In the uplink, we don't have a choice other than using short preamble (where M = D = 128).
For fine frequency-offset estimation (both in the uplink and downlink), the second symbol is used where better noise averaging can be obtained by using a block of 128 (i.e, M = D = 128). In the uplink, there isn't any other choice than in using this symbol anyway.
Once the frequency offset is calculated, the received time samples can be rotated in the opposite direction of the estimated frequency offset to compensate the effect of the frequency offset, i.e.,
Timing synchronization refers to finding the exact timing instant of the beginning of each OFDM symbol. Unless the correct timing is known, the receiver cannot remove the cyclic prefixes at the right timing instant of the symbol and separate individual symbols correctly before computing the FFT of their samples. Timing synchronization algorithm basically fine-tunes the rough symbol timing obtained by the packet detection algorithm. Fine symbol timing is calculated by using the short training sequence. Cross-correlation between the received signal and known reference is calculated. In this case, we obtain the optimum timing position when the cross-correlation is maximum. However, due to multipath components, it is possible to observe multiple peaks. Also, the largest peak might not correspond to the first multipath component. Therefore, an additional fine tuning of the symbol timing is needed for multipath channels. We use joint channel estimation and symbol timing estimation for fine tuning of the symbol timing estimate.
Figure 12 shows the cross-correlation between received signal and known reference. The peak, where maximum occurs, clearly shows the correct timing point for a flat fading channel (a single multipath component). However, when the channel is frequency selective, multiple peaks can be observed. Figure 13 shows the cross-correlator output for frequencyselective channels.
The packet-end detection and packet-extraction block detects the end of a packet, specifically important for measurement purposes (not an integral part of a regular receiver). If FCH information content is not available, this is an important block that detects when the useful information in the RF burst ends. If FCH content is available, or some side information about the RF burst is given as an input, we can turn off the packet end detection calculation. Otherwise, we need to turn it on so that we don't decode and measure the noise part in the received signal.
The algorithm takes advantage of the gaps before and after the RF burst to determine the end of the RF burst. Before the RF burst is turned on, a short gap that is purely noise is used to calculate the noise power. Since we have detected the beginning of the RF burst, we can also calculate the signalplusnoise-power after the starting point of the RF burst (note we use the data after the preamble for this purpose, i.e., skip the preamble). A short period (one OFDM symbol length of data) is enough for calculation of signalplusnoise-power. Using these two calculated pieces of data, it was possible to develop a decision metric to find the end of the packet.
The first step is to determine the signal-to-interference-power ratio (SNR) using the noise power measured before the packet start and signal power after the packet start (the noise power is ignored during the packet transmission assuming that signal power is much larger than the noise power):
where:
W = a window of samples (which in our case is the number of samples for one OFDM symbol length namely 256).
The SNR is monitored over nonoverlapping block of samples for all the receive samples. (For computational complexity reduction, nonoverlapping blocks are used; however, sliding windowing is also possible). Then, the SNR values are compared for each block with respect to the SNR value given above. When the SNR drops below a threshold value, it is declared as the end of the package. The choice of threshold is a design criterion.
Channel estimation is an integral part of many coherent wireless-communication receivers. There are many advanced channel-estimation techniques available in the literature. A very simple channel estimator was employed here. In this work, the channel is assumed to be almost constant during a data packet as explained earlier. A simple least-squares (LS) channel estimator with a sliding window noise averaging is used for channel-frequency estimation. The LS estimates can be given as:
where:
Xpilot = the known carrier symbols in the preamble.
Page Title
The preamble symbol with two identical repetitive blocks is used for channel estimation. As mentioned earlier, in this training symbol, one carrier is skipped (nulled) after a pilot carrier (i.e., total number of known pilot carriers is 100). Therefore, it is necessary to perform an interpolation to find the channel values in the nulled carriers. A simple linear interpolation is used in the proposed receiver. After the interpolation, a sliding window filtering is applied to reduce the noise effect in the estimates. Note that the sliding window size needs to be chosen carefully. If the window size is large, the channel estimates will not be good for highly dispersive channels. On the other hand, if the window size is small, optimal noise suppression cannot be obtained.
During the data transmission, channel equalization is employed to remove the effect of the channel from the received samples. The channel equalization can be performed as:
In pilot tracking, common phase estimation, sample timing estimation, and common gain tracking are performed. The phase rotation in the received signal is estimated and corrected for each OFDM frame using eight pilot symbols. The average phase difference between transmitted and received symbols is found by multiplying the received pilots with the conjugate of reference pilots and finding the phase of the result. Once the phase rotation is estimated, it can be corrected easily. Common gain error is also estimated in a manner similar to above by comparing the gain differences between the transmitted and received symbols. The sample timing error is a little bit tricky which needs to take into account the variation of the phase both in time and frequency. In our receiver, we used the phase differences in time and frequency to calculate the sample timing error.
To detect the transmitted symbols correctly, the receiver must know which type of modulation is being used at the transmitter. This information is included in FCH content; however, if the FCH is not available or the receiver cannot decode it, blind modulation detection is necessary. Blind modulation detection has been traditionally approached in two ways, namely pattern recognition and decision theoretic approach. 14 In statistical pattern recognition methods, several recognized pattern recognition algorithms such as Fuzzy C-means clustering15 have been proposed and tested to perform well, provided that there are a relatively large number of samples available to make a decision.
The object of blind modulation detection is to determine the type of modulation used with the information conveyed by the least possible number of received samples. The only empirical data provided by the received noisy samples is the distance to the closest legitimate constellation point of all possible modulation schemes. In other words, given a noisy sample, there would be M errors where M is the number of modulation schemes used. Therefore, the objective is to make use of the distribution of these empirical data or errors, to make a statistical inference of the type of modulation used.
One technique for blind modulation detection, which is given in ref. 16, is based on the decision theoretic approach. The mean Euclidean distances between the received samples and all the closest legitimate constellation points of all possible modulation schemes are calculated. The average Euclidean distance for different hypotheses can be calculated as:
where:
Y = the received sample,The scheme which minimizes the average Euclidean distance, e, is chosen for demodulation (Eq. 24). However, there is always a bias toward the higher-order modulation schemes irrespective of the actual modulation used. The reason for this is that there are closer legitimate points for higher modulation schemes which would yield lower errors.
To compensate the bias, information theoretic approaches are proposed in the literature such as Akaike Information Criteria (AIC) and Bayesian Information Criteria (BIC). The authors have also used such a technique in the proposed receiver. Based on exhaustive measurements, the authors have developed their own information criteria. Similar to the above approach, the method involves first calculating the error terms corresponding to each modulation hypothesis. Then, a correction term is introduced as:
where:
b = a constant, 0.9 in the current case and Mm = the constellation size of the mth modulation hypotheses.
The resulting detected modulation is the one that minimizesFCH decoding is very useful as the transmission parameters defining the burst profiles (like modulation and coding used, burst length) are contained in FCH. With the ability of FCH decoding, more accurate test and measurement capabilities can be achieved. FCH contains the Downlink Frame Prefix (DLFP) that specifies the modulation type and number of symbols associated with one or several downlink bursts that follow the FCH. The modulation and coding used in the first downlink burst immediately following the FCH is specified in the RateID. The RateID is a 4-b code. The Downlink Interval Usage Code (DIUC) is a 4-b code similar to the RateID and is used for identifying the profiles of the other bursts in the downlink. The DLFP also includes an 8-b Header Check Sequence (HCS), which is used to detect errors.
FCH decoding requires demodulation, de-randomization, decoding, and deinterleaving of the received samples. In addition, the CRC decoder is also required to check whether the content of the decoded bits is correct or not. In other words, in order to be able to decode FCH content, a full standards-based receiver is needed. The proposed receiver incorporates the FCH decoding capability. Once the FCH content is decoded, it needs to be separated into its associated fields. The IEEE 802.16-2004 standard provides the description of FCH decoding content.
Editor's Note: This is the second installment of a three-part article series on WiMAX measurements. Next month, the final part of the series will examine some of the measurements that can be performed with the experimental WiMAX test receiver constructed this month.
ACKNOWLEDGEMENT
The authors would like to thank Dr. Larry Dunleavy for his comments and for the review of this article prior to publication.