Download this article in .PDF format
The Y-factor is the ratio of output noise power from a device under test (DUT) with the noise source set to hot, divided by the output noise power with the noise source set to cold. Using the Y-factor approach, the noise figure of a DUT can be calculated by using Eq. 1:Manual noise-figure measurements are often necessary when automated measurement systems are not available. One of the more popular techniques for making noise-figure measurements is the Y-factor method, which is accomplished with the aid of a hot/cold noise source to provide two different noise power levels (for this article, cold will be assumed at 290K). The difference between the two noise power levels is the excess noise ratio (ENR), which is given numerically by (TH - Tc)/ Tc, where TH represents the hot temperature and Tc is the cold temperature. Under true impedance-matched conditions, the actual available noise power would be equal to kTB, where k is Boltzmann’s constant (1.3806503 × 10-23m2kg/s2K), T is the temperature (in degrees Kelvin) or S/B (in Kelvin), and B is the bandwidth of the circuit under test.
Noise figure of DUT = 10log10[ENR/(Y - 1)] (1)
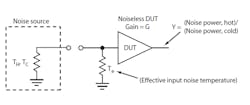
where ENR is the numerical ratio of the ENR in dB, or ENR = 10(ENR/10). The ENR is defined as (TH - 290)/290. Figure 1 shows a typical setup for measuring the Y-factor. The resistor in the noise source is a fictitious component with a body temperature that can be changed to produce different levels of output noise power. The resistor at the input of the DUT, TE, represents a fictitious resistor at a temperature of TEK that, when multiplied by the gain of the DUT, would produce the proper amount of noise at its output corresponding to its internally generated noise. The input noise temperature is related to the noise figure by Eq. 2:
TE = 290(NFac - 1) (2)
where NFac, the noise factor, is the numerical value of the noise figure—e.g., NFac = 10[(Noise Figure)/10].
1. This basic circuit is used to evaluate the Y-factor of a DUT when using a calibrated noise source.
As shown in Fig. 1, the standard circuit for a noise figure measurement is simple and can provide an accurate measurement of the DUT’s noise figure if one were able to accurately measure the output noise power of the DUT. Since an instrument must be used to make the noise power measurement at the output of the DUT, the noise power measurement is a composite of the noise power coming out of the DUT, along with the internal noise generated by the measuring device (for manual measurements, the measuring instrument is usually a spectrum analyzer).
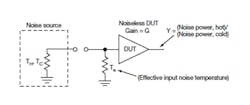
2. A spectrum analyzer can also be used for measuring the noise figure of a DUT.
Making a noise-figure measurement
Spectrum analyzers usually have a large noise figure in the 20-to-30-dB range or, for more sophisticated instruments with an internal preamplifier, the noise figure may be reduced to the 10-to-15-dB range. The typical procedure for making a noise-figure measurement is to first measure the noise figure of the spectrum analyzer by placing the noise source directly on the analyzer’s input port. A measurement is then made with the DUT placed between the noise source and the input to the spectrum analyzer, as shown in Fig. 2. Once the two measurements have been made, the noise figure of the device is calculated from the following equations:
Noise factor of spectrum analyzer = ENR/(YSA - 1) = NFacSA (3)
Total noise factor of the DUT plus the spectrum analyzer:
NFacTOTAL = ENR/(YTOTAL - 1) (4)
Noise factor of the DUT = NFacTOTAL - (NFacSA - 1)/GDUT (5)
where GDUT is the gain of the DUT.
The novel noise-measurement approach about to be described follows the procedure for first characterizing the noise figure of a spectrum analyzer, and then evaluating the noise of a DUT in cascade with the analyzer. One important difference is that results with the new method are obtained by means of the derivative of the Y-factor. Measurements are independent of the absolute value of the input excess noise level to the DUT and eliminate the need for a calibrated noise source.
NFac = ENR/(Y - 1) (6)The new method begins with the standard equation for the noise factor of a DUT, given the ENR of the noise source and a Y-factor measurement as detailed in Eq. 6:
Rearranging terms results in Eq. 7:
Y = ENR/NFac + 1 (7)
Taking the derivative of each side with respect to the ENR yields Eq. 8:
dY/dENR = 1/NFac (8)
This results in Eq. 9:
NFac = 1/(dY/dENR) (9)
What this shows is that the noise factor can be determined without knowing the absolute ENR; only the difference in ENR, which results in a difference of the Y-factor measurement, is needed for the calculation. This new noise factor approach consists of making two Y-factor measurements at two different noise power levels at the input of the DUT. These two Y-factor values, along with the corresponding source noise power values, provide the information needed to construct the ΔY and ΔENR values. These will produce the slope or dY/dENR, and in turn produce the noise factor result according to Eq. 9.
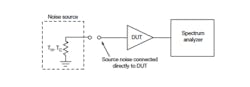
The method used to vary the ENR involved using an arbitrary source of noise power (e.g., a high-gain amplifier) with its noise output level controlled by a step attenuator. This produces a range of ENR values based on the setting of the step attenuator. This method does not require knowledge of how much noise power is being generated, nor details about the attenuation characteristics of the step attenuator. The only purpose of the noise source/attenuator is to provide two different levels of noise power. This also means that a cable with unknown loss characteristics can be used to connect the noise source/attenuator to the DUT without impacting the noise-figure calculations.
3. A spectrum analyzer can also be used when measuring the change in ENR of an uncalibrated noise source to check the noise figure of a DUT.
Determine the change in ENR at a DUT’s input
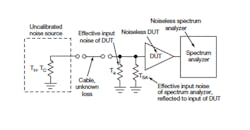
The key to this new noise measurement approach is to determine the change in ENR at a DUT’s input, using power readings from the spectrum analyzer translated to the input plane of the DUT. For example, if the spectrum analyzer reads -121 dBm, and the gain between the input to the DUT and the input to the spectrum analyzer is 15 dB, then the translated noise power at the input reference plane of the DUT would be -136 dBm. The noise temperature model of Fig. 3 shows how the internal noise power generated by the analyzer can be translated to the input reference plane of the DUT as an effective input noise temperature. The effective input noise power at the input to the DUT is a composite of three sources:
1. The input noise power (generated by the noise source);
2. The effective input noise power of the DUT (related to the noise figure of the DUT); and
3. The effective input noise power of the spectrum analyzer translated to the input of the DUT (related to the noise figure of the spectrum analyzer).
This can be written as:
Pn1 = KB(TH1 + TDUT + TSA) (A)
and
Pn2 = KB(TH2 + TDUT + TSA) (B)
where P(p)n1 is defined as the effective input noise power into the DUT for different values of hot input temperature, THi, and is determined from the measurements by the simple equality
P(p)ni = 10[(PdB MEASURED - GaindB)/10]
and where parameter GaindB represents the small-signal gain (in dB) from the input of the DUT to the input of the spectrum analyzer.
Taking the difference of the two noise powers, P(p)n2 - P(p)n1, yields Eq. 10:
ΔPn = KB(TH2 - TH1) → (TH2 - TH1 = ΔPn/KB) (10)
At this point, it is necessary to solve for ΔENR by means of Eq. 11:
ENR1 = (TH1 - 290)/290
and
ENR2 = (TH2 - 290)/290 → ΔENR = ENR2 - ENR1 = (TH2 - TH1)/290
and from Eq. 10,
→ ΔENR = ΔPn/(290KB) (11)
Parameter dY can be calculated from Eq. 12:
Y1 = 10(Pn1 - Pn0)/10)
and
Y2 = 10(Pn2 - Pn0)/10)
where Pn is in dBm (12)
where Pn0 is the noise power measured on the spectrum analyzer with an input noise power to the DUT of 290 K (the input of DUT terminated with a matched load at 290 K):
→ ΔY = Y2 - Y1 (13)
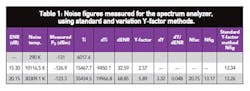
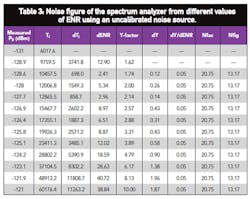
The first set of data appearing in Table 1 is the measurement of the spectrum analyzer’s noise figure (with the preamplifier turned on) using two calibrated noise sources. The last column shows the result of using the standard Y-factor method for the two different ENR noise heads. The next-to-last column shows the result using the method described in this article. The set of data shown in Table 2 shows the result of using the new method with dENR determined by taking the difference in ENR of the calibrated noise sources. Table 3 shows the results for the spectrum analyzer’s noise figure for different values of ENR obtained from an uncalibrated noise source (about a 22-dB-gain amplifier). This is obtained by using a variable attenuator whose output is connected to the spectrum analyzer through a test cable.
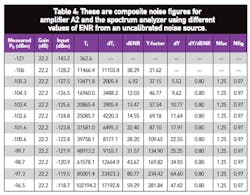
The remaining data show the results for two amplifiers with noise figures measured at 1.62 GHz with a model HP 8970A noise figure test set from Hewlett-Packard (now Agilent Technologies). The two amplifiers yielded a noise figure of 2.60 dB and gain of 11.6 dB for amplifier A1 and a noise figure of 0.55 dB and gain of 22.2 dB for amplifier A2. Table 4 shows the total noise figure of amplifier A2 together with the spectrum analyzer. By applying Eq. 5, the actual noise figure of amplifier A2, NFacA2, can be calculated as:
NFacA2 = 1.25 - (20.75 - 1)/165.96 = 0.54 dB
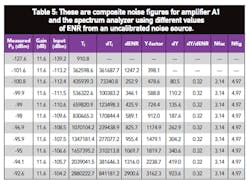
Table 5 shows the total noise figure of amplifier A1 together with the spectrum analyzer. By applying Eq. 5, the actual noise figure of amplifier A1, NFacA1, can be calculated as:
NFacA1 = 3.14 - (20.75 - 1)/14.45 = 2.50 dB
In summary, a manual noise figure test method has been presented which eliminates the need for a calibrated noise source. The method is as accurate as the previous Y-factor method, while eliminating the expense and calibration routine associated with a calibrated noise source. The method allows the use of a lossy test cable to connect the noise source to the DUT without any need to account for the cable’s loss in the noise figure calculations. As with the standard Y-factor method, the accuracy of this method will also depend upon such parameters as measured gain accuracy, ambient room temperature, and VSWR of the DUT and other interconnecting components. The effect of these parameters is beyond the scope of this article, but can be researched in the multitude of articles written about the standard Y-factor method.