Passive Standards Aid Noise System Verification
Amplifier and oscillator designers can benefit from load-pull and noise test sets by using them to vary the load and source impedances to a device under test (DUT). Such test sets must be verified, however. Load-pull test sets are verified by using a “back-to-back” or “DeltaGt” verification method as an objective measure for accuracy. Noise test sets instead require some form of noise standard. Active noise standards, such as noise sources based on avalanche diodes, must be calibrated in specially equipped standards laboratories; one such facility is the National Institute of Standards & Technologies (NIST) in Boulder, CO.
Related Articles
• Filtering EMI And RFI Noise
• Cross-Spectral Phase Noise Is Measured On Terahertz Source
• REVEALED: Source Of Low-Frequency 1/f Noise
Passive noise standards are easier to use for verification, since passive components exhibit a noise figure and generate available power as white thermal noise. Almost any attenuator or termination can serve as a passive noise standard. In the case of either active or passive noise standards—namely, the four noise parameters—the small-signal electrical and physical properties must be precisely known so that its noise characteristics can be determined at a known and controlled temperature. These parameters are minimum noise factor (Fmin), noise resistance (Rn), magnitude at optimum impedance match (|Γopt|), and phase at optimum impedance match (∠Φopt).
An avalanche diode is an example of an active device used as both a noise source and a noise calibration standard. Noise-figure measurements require a source of two noise power levels, which the diode can provide when biased on and off. It is a suitable active device for measuring noise figure (F) in amplifiers and other DUTs. It is typically teamed with some form of radiometer or measurement receiver—such as a spectrum analyzer or noise-figure meter—to perform the noise measurements.
Practical noise standards are those that users can produce themselves, created from known materials and with known dimensions. Attenuators with different values, such as 3 and 6 dB, have been used as passive noise standards for tuner-based four-noise-parameter test sets.
Noise measurements are never routine, whether making them in impedance-matched or unmatched conditions. Nevertheless, measurement accuracy is always vital, as is collecting adequate data from a noise measurement system for processing. In calculating the noise factor, F, the known noise of a noise standard can be used to measure the difference between the signal-to-noise ratio (SNR) of a DUT at the input and at the output of the DUT:
F = (Sin/Nin)/(Sout/Nout) (1)
where:
Sin = the input signal level;
Nin = the input noise level;
Sout = the output signal level; and
Nout = the output noise level.
Focus Microwaves has developed a number of measurement system solutions for verification, with different types of matched networks (fixed attenuators) or mismatched networks used as passive noise standards. Of course, the ambient temperature must be known and the electrical RF parameters in form of scattering (S) parameters of such networks must be accurately measured, to be able to calculate the theoretical noise parameters and compare with the noise parameters then measured by the noise system.1
Because of Eq. 1—and considering that a passive network produces the same available output thermal noise power, Nout, as it receivers at its input, Nin, or Nout = Nin—the noise factor, F, can be described as a ratio of available signal powers, F = Sin/Sout. And since only “available” power is considered, then F = 1/available gain = available loss, as given by Eq. 22:
F = [|1 - ΓS*S11|2 * (1 - |Γ0|2)/(|S21|2 * (1 - |ΓS2)] (2)
where:
Γ0 = S22 + S12 * S21/(1 - ΓS * S11);
ΓS = (1 - ys)/(1 + ys);
ys = Ys/ Y0, with Y0 = 20 mS; and
Sij = the S-parameters of the network.
It is therefore straightforward to compute the four noise parameters of a passive network by calculating F for at least four source impedances and solving the four equations for minimum noise factor (Fmin), equivalent noise resistance (Rn), and optimum source reflection factor (Γopt).
Verification Approaches
Noise measurement system verification includes the following two methods:
1. Verification of exraction math using matched standards, such as passive 3-, 6-, and 9-dB attenuators; and
2. System accuracy is verified using mismatched standards, such as passive bandpass filters.
Noise measurements are dispersive. This is essentially due to the small power levels being measured compared with environmental spurious levels. Because of this dispersion, four source impedance data points are never enough for any measurement. Typically, a higher number of data points are measured and noise-parameter extractions are effectuated, often yielding slightly dispersive results.
Mathematical and statistical methods, such as singular value decomposition (SVD) are applied to extract the correct information from the dispersive raw data.3,4 The comparison of noise parameters extracted from measured dispersive data points using SVD with theoretically known results shows that the math is capable of extracting the correct information (even if at first view the data seem random).
In general, the SVD method computes a least-squaressolution of an over-defined, linear system of equations. As such, this method computes the pseudo-inverse of the corresponding matrix (which represents the aforementioned system of equations) and uses this result to produce a solution. The Focus Microwaves standard noise parameter extraction method uses SVD analysis of the measured noise-figure data (produced by noise-figure measurements under various source impedances) to determine the noise parameters.
The disadvantage of the SVD method (and matrix inversion operations in general) is that a few incorrect data points can cause the final solution to vary wildly, or even fail completely. This can occur in noise-figure measurements, particularly if the DUT oscillates, or if the linearity of the noise receiver is somehow compromised in a few of the measured data points. This can occur if a noise receiver is operating under compression or if the power density level is too low to be distinguished from the thermal noise floor.
The solution in these cases is to measure more points and remove their effects on the final noise parameter solution. This is accomplished in the Focus Microwaves software by using a “statistical extraction” method. Specifically, the software selects many different subsets of the measured data and performs an extraction (i.e., determines a set of noise parameters) on each subset. Mathematically, these subsets correspond to the selection of many “combinations without repetition” of the measured data points. This produces several million solutions (sets of noise parameters). These solutions are then filtered, ranked, and statistically analyzed to determine the final set of noise parameters. In this way, the effects of a few incorrect data points on the overall solution are minimized.5,6
Noise standards provide an independent verification tool for noise system calibration and measurement accuracy. Noise parameters produced from noise standards are easily verified, both via measurements and mathematical calculations of the noise parameters for passive components. Matched attenuators are straightforward to measure; there are no noise power reflections created between the DUT (the attenuator) and the receiver, reducing the requirements for receiver dynamics. If the extracted noise parameters based on measured data correspond to the noise parameters calculated for the DUT’s S-parameters, the system is considered accurate under matched conditions.
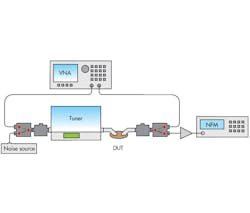
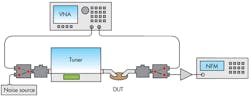
Figure 1 illustrates the experimental setup of a noise parameter measurement. This setup performs both S-parameter and noise-parameter measurements of a DUT, without removing and/or reconnecting any component, by configuring the input and output switches in the correct paths. For the measurements, the DUTs were a set of passive, 50-Ω matched attenuators with values of 3, 6, and 9 dB. Figures 2-4 show theoretical and measured noise-parameter results for the attenuators.
Multiple measurement samples were taken consecutively for each DUT to evaluate the repeatability of the noise test system. As the test results show, the maximum variation of Fmin is 0.16 dB or ±0.08 dB, occurring at the highest frequency (26.5 GHz). The variation is due to the uncertainty in reading the noise power from the power detector of the noise figure meter.
For the Agilent PNA-X VNA with noise option used for this testing, the measured variation is comparable with the dynamic accuracy of the noise receiver over an 8-MHz bandwidth. The variation of noise resistance is well within 2.5%. The repeatability and accuracy of Γopt are excellent in all cases. Since these attenuators are well matched (25 dB or better return loss), the Γopt points are all in the center of the Smith chart. While it is difficult to find the correct phase for Φopt, Focus’ extraction math accurately predicts the values of Φopt in all cases.
Practical Considerations
While measuring passive matched noise standards can be useful for verifying a test system setup, as well as the noise extraction algorithm, it might not always represent the reflection characteristics of practical active devices such as field effect transistors (FETs). In the case of a FET, the input and output terminals exhibit capacitive behavior and often represent a nearly open circuit at frequencies to tens of gigahertz. To mimic this behavior, a two-port, passive non-matched bandpass filter was built and used as a non-matched standard for noise measurements.
(a)
(b)
Figure 5 shows the S-parameter response of such standard and a photograph of the prototype network. Measured results of passive, non-matched standards further confirm the repeatability and extraction accuracy of the Focus Microwaves measurement system under extreme mismatched conditions—a very important figure of merit for evaluating a noise-parameter measurement system.
Related Articles
• Filtering EMI And RFI Noise
• Cross-Spectral Phase Noise Is Measured On Terahertz Source
• REVEALED: Source Of Low-Frequency 1/f Noise
Mismatched attenuators are generally difficult to measure because there is no DUT gain, and the noise power reaching the receiver is reduced due to the impedance mismatch. The dynamic range of the measurement system must be wide so that the noise level being measured remains above the detection limit of the receiver. Extraction algorithms in this case must be more robust compared to what was required under matched conditions, pushing the limits of the measurement system accuracy to the extreme levels. If the extracted noise parameters based on measured data correspond to the noise parameters calculated out of the S-parameter for the DUT (the mismatched attenuator), the system is considered accurate.
For those working with noise measurement systems from Focus Microwaves, the matched and non-matched passive noise standards developed at the company serve to verify the repeatability and accuracy of those test systems. By using these passive standards, those using the test systems can gain confidence in the accuracy of their measurements on active devices.
Hoang V. Nguyen, Manager, RF Engineering
Neven Misljenovic, Supervisor, Installations and Training
Bryan Hosein, Manager, Software Engineering
Christos Tsironis, President
Focus Microwaves, Inc., 1603 St. Regis, Dollard-des-Ormeaux, Quebec, Canada H9B 3H7; (514) 684-4554, FAX: (514) 684-8581.
References
1. Hoang V. Nguyen, Neven Misljenovic, Bryan Hosein, and Christos Tsironis, “Noise System Verification using Noise Passive Standards,” 18th Journees Nationales Microondes, Paris, France, May 14-17, 2013.
2. David M. Pozar, Microwave Engineering, 2nd ed., Wiley, New York, 1998.
3. R. Lane, “The determination of device noise parameters,” Proceedings of the IEEE, Vol. 57, No. 57, August 1969, p. 1461.
4. Vahe Adamian and A. Uhlir, “A novel procedure for receiver noise characterization,” IEEE Transactions on Instruments & Measurements, Vol. IM-22, No. 2, June 1973, pp. 181-182.
5. Hoang V. Nguyen, Neven Misljenovic, and Bryan Hosein, “Efficient noise extraction algorithm and wideband noise measurement system from 0.3 GHz to 67 GHz,” Automatic RF Techniques Group (ARFTG), 81st Microwave Measurement Conference, Seattle, WA, June 2013.
6. Anonymous, “Noise measurements using the computer controlled microwave tuner system,” Application Note 1-90, Focus Microwaves, Inc.