Forming Low-Impedance MEMS Bandpass Filters
Download the PDF of this article.
Bandpass filters based on microelectromechanical structure (MEMS) technology potentially offer reliable electrical performance in small sizes. MEMS bandpass filters can be manufactured in several ways and, to compare two methods, filters were developed using single-annular-resonator (SAR) and soft mechanically-coupled-annular-resonator (MCAR) modules. The prototypes had center frequencies at 850 MHz and 2.4 GHz and featured close agreement between their simulated and measured characteristics. The main difference in the two MEMS filter approaches is the wider bandwidth provided by the soft MCAR filters.
Bandpass filters with small sizes have been produced in a number of ways, including with piezoelectric techniques and with capacitor arrays. The use of piezoelectric components, such as crystals and film bulk acoustic arrays (FBARs), yield high quality-factor (Q) bandpass filters as used in cellular telephones. However, the frequency of a piezoelectric component is determined primarily by its thickness, making it difficult to achieve multiband filters on the same chip without separate structural film depositions. In addition, FBAR filters are usually bulky compared with MEMS filters, which may limit their use in future mobile communications applications.
MEMS capacitive membrane switches have been used in bandpass filters covering 110 MHz to 2.8 GHz (Fig. 1).2 Variable capacitor structures have been employed in multipole lumped-element bandpass filters, but the passband insertion loss has been between 6.6 to 7.3 dB through 2.8 GHz, which not acceptable for modern wireless communications applications. This design technique also suffers low Q and requires a space-consuming inductor.2
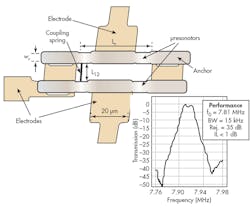
High Q bandpass RF filters using MEMS oscillators have also been explored by various researchers. They are usually compact in size and require few components with lower cost than traditional filter designs.3Figure 2 shows a typical filter fabricated with this technique.4 The approach yields passbands around 8 MHz with Qs from 40 to 450 (percent bandwidths from 0.23% to 2.5%). Passband insertion loss is less than 2 dB, with spurious-free-dynamic-range (SFDR) performance of 78 dB. Unfortunately, this approach results in filters with high input and output termination resistances, on the order of 12 kΩ.4 In general, this type of high impedance is a major barrier to the use of MEMS filters in RF applications.
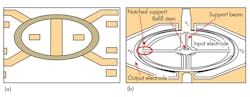
Separate efforts at the University of California at Berkeley and the University of Michigan investigated low-impedance MEMS filters using the radial bulk annular resonator (RBAR) concept (Fig. 3).5,6 In concept, the approach can readily achieve impedance of less than 50 Ω, and the frequency of an RBAR filter has first-order independence of thickness. Both research groups worked with high-temperature processed polysilicon (poly-Si) as the resonator material. The material is difficult to handle during fabrication, and no low-impedance filters were fabricated successfully. In addition, although the RBAR approach can achieve very high Q (14,603 at 1.2 GHz), its single-resonator structure exhibits a narrow bandwidth not suitable for modern communications applications.6
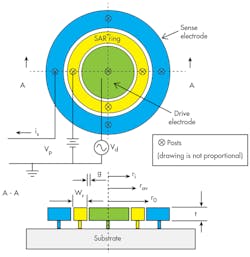
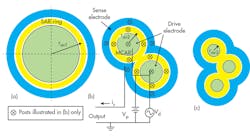
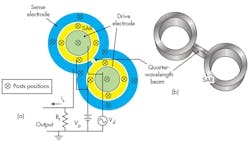
To achieve low-impedance RF bandpass filters, original research was performed by the authors on the mechanically coupled annual resonator (MCAR) concept. The main component of an MCAR design is a single annular resonator (SAR), which is similar to an RBAR (Fig. 4). It consists of a drive electrode, an SAR ring, and a sense electrode. Each is attached to the substrate by four posts.
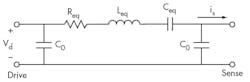
The operating principle of a SAR is simple: electrical input signals are converted to mechanical energy, processed (with high Q) in the mechanical domain, and then converted back to electrical signals at the output port for further processing by subsequent communications transceiver stages. For operation, a dc bias voltage, Vp, is applied to the SAR ring and an ac signal, Vd, is applied to the drive electrodes (Fig. 4). Voltage Vd generates an electrostatic force radially on the SAR ring at the ac input frequency. When the frequency of Vd matches one of the ring’s resonant frequency modes, the ring starts to vibrate. An SAR can be modeled electrically as a parallel LCR circuit (Fig. 5).3,5,7,8
As reported in ref. 4, Eq. 1 is valid for rqv >> Wr, e.g., rqv > 2Wr:
f ≈ (1/2WV)(E/ρ)0.5 (1)
where E is Young’s modulus and ρ is the mass density of the SAR material. Equation 1 indicates that the resonant frequency is independent of thickness, t. Thus, a SAR’s resonant frequency is insensitive to process variations in thickness. As a result, filters with different frequencies for multiband and RF channel-selection applications can be fabricated with one structural film deposition on one chip. This is a distinct advantage over most piezoelectric counterparts (e.g., FBAR and crystal filters), which require distinct material thickness to correspond to certain frequency. To build filters with multiband frequencies via the piezoelectric approach requires several structural film depositions and patterning for different frequencies.5
For rqv >> Wr, the impedance, Req, is given by Eq. 2:
Req = [(Eρ)0.5/Qπε02] (g4/2πravtVP2) (2)
where Q is the quality factor, ε0 is the permittivity of a vacuum, VP is the resonator bias voltage, t is the thickness of the structural film, and g is the gap width of the drive and sense capacitors (Fig. 4). Equation 2 indicates that Req for an SAR is inversely proportional to the average radius and independent of Wr, and the insertion loss is independent of its resonant frequency.9
To save die area, several small SARs can be combined to form an MCAR rather than fabricated one large SAR. A shown in Fig. 6, rav1(a) = 2rav2(b) = 3rav3(c). Because the MCAR in b consists of 2 SARs, and the MCAR in (c consists of 3 SARs, both MCARs have the same capacitive area as the single SAR of a. Obviously, as the number of SARs in an MCAR increases, the area of the MCAR shrinks for the same capacitive area. It should be noted that this area shrinkage is not unlimited, because the frequency value from the Eq. 1 only valid when rav > 2Wr. In other words, the inner radius of the SAR ring should be at least two times larger than the width of the SAR ring.
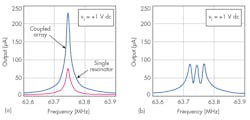
One method for lowering the impedance (motional resistance) of MEMS resonators is to combine currents from several resonators to produce a larger summed current. This can be done by connecting several resonators with identical frequency responses in parallel and driving them with the same input source, vd. The total current through the resonator array for the same input voltage vd is the individual resonator output current times the number of resonators in the array (Fig. 7a). The impedance is reduced by increasing the number of resonators.8-10
In reality, dimensional variations of resonators is unavoidable due to process variation, and these physical variations will cause variations in the frequencies of resonators even when they are on the same wafer. A small mismatch in the frequency of the resonators in an array (i.e., 0.01%) can dramatically impact the signal output (Fig. 7b). The high ripple is unacceptable for most communications applications.
Mechanical coupling offers a superior solution to the mismatching problem. Multiple (n) resonators can be coupled mechanically, such as the MCARs shown in Figs. 6b and c, to achieve a mechanical filter structure. Soft-spring-coupled resonators exhibit n modal frequencies, and each mode corresponds to a specific frequency and modal shape.7, 9, 11 In contrast, stiff-coupled resonators automatically generate a single resonance response (i.e., mode) from all resonators, without the need for absolute matching of individual resonator responses.12
8. This is the passband and rejection band of an ideal bandpass filter.
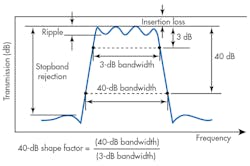
A stiff coupling structure may not increase the bandwidth, but many applications require only a small percent of the bandwidth. An industry-acceptable bandpass filter should have flat passband response, sharp rolloff, and high stopband rejection (Fig. 8). To achieve these qualities, a “soft MCAR” concept was developed for bandpass filters. In a soft MCAR, the SAR rings are coupled by a one-quarter-wavelength coupling beam, which acts as a soft coupling spring. As shown in Fig. 9, two adjacent SAR rings are connected with a beam which is about one-quarter wavelength in length. The quarter-wavelength coupling is a state-of-the-art technique used to expand the bandwidth.8
Under a quarter-wavelength condition, the coupling beam dimension should satisfy the condition of Eq. 3, and its stiffness will be determined by the beam dimensions (Eq. 4):
sinh(α)cos(α) + cosh(α)sin(α) = 0 (3)
The relationship between the bandwidth (B) for a filter with center frequency f0 and various stiffnesses is shown by Eq. 413 :
B = (f0/kc)(ks/kr) (4)
where kc is a normalized coupling coefficient derived from a ratio of resonance and 3-dB cutoff frequencies in a lowpass prototype for the desired filter, and is listed in filter cookbooks.14 The coupling beam stiffness is determined by the beam dimensions (Eq. 5):
Ks = [EIsα3(sinα + sinhα)]/{Ls3[cosα(coshα – 1)]} (5)
with
α = Ls[ρWshω2/(EIs)]0.25
and
Is = Wsh3/12
where Ws is the width of the beam; h is the thickness of the beam; and Ls is the length of the beam. Similarly, the resonator stiffness can be calculated from its dimensions.15
The quality factor Q can be calculated from Eq. 68:
Q = 1/PBW = kc(ks/kr) (6)
where Pbw is the percent bandwidth and Q is determined by the soft coupled structure. The resistance of the termination resistor Rt can be calculated from Eq. 75:
Rt = Rr{[Q/(qtQftr)] – 1} (7)
where Q is the unloaded quality factor of the constituent resonators; Qfilter = f0/B; Rr is the series motional resistance [which can be obtained from the actual filters using a vector network analyzer (VNA)]; and qt is a normalized parameter that can be obtained from a filter cookbook.14
From Eq. 6, the ratio of kr/ks is another factor that provides sufficient percentage of bandwidth (PBW). Parameter kc is a normalized coupling coefficient derived from a ratio of resonance and 3-dB cutoff frequencies in a lowpass prototype for the desired filter, and is listed in filter cookbooks.14 For a filter with 0.5-dB ripple, kc is 0.72.14 Parameter kr is a dynamic resonator stiffness factor and is a function of locations along resonator length between two restraining anchor posts, as shown in Eq. 88:
kr = [(Ewrh3)/4][(1/Lr3) + 1/(Lr0 – Lr)3] (8)
where E, w, and h are Young’s modulus, the width of the resonator, and the height of the resonator, respectively. Parameter Lr0 is the partial circumference (e.g., the length between two adjacent posts) of the resonator ring.
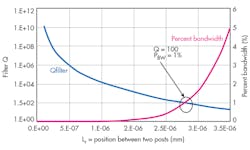
According to the process constraints of the fabrication facilities, the coupling beam dimensions were Ls = 1 μm, Ws = 1 μm, and h = 2 μm. In this case, the quarter-wavelength conditions (Eqs. 3 and 4) were satisfied, with a kr/ks ratio of 7 × 10-7. The Qfilter and PBW versus coupling position were simulated (Fig.10). The coupling beam was placed very close to the anchoring post at Lr = 2 to 3 μm, with PBW = 1% and Q = 100.
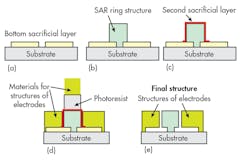
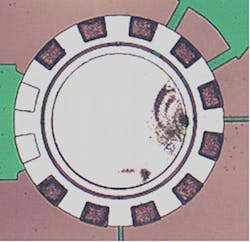
Aluminum was selected as the ring and electrode material for the SAR, and Si wafers covered with oxide were used as substrates. Figure 11 shows the process flow. Two sacrifice layers of different materials were used in the process as shown in Figs. 11a and c. Figure 12 shows a scanning electron microscope (SEM) shot of the processed resonator ring.
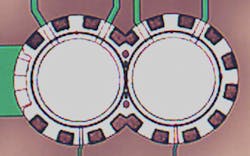
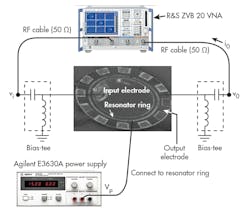
Images of the final fabricated SAR and soft MCAR filters are shown in Figs. 13 and 14, respectively. A commercial vector network analyzer (VNA), a model ZVB 20 from Rohde & Schwarz with frequency range of 10 MHz to 20 GHz and a DC power supply, a model E3630A from Agilent Technologies (now Keysight Technologies), were used for RF testing (Fig. 15).
A probe station was used for the on-wafer RF measurements. A customized setup was used to maintain the resonator under low vacuum conditions during measurements. A rubber tube connecting the mechanical vacuum pump at 6 mTorr was manually positioned at the resonator location to provide the vacuum environment.
The current research work has focused on demonstrating SAR and MCAR concepts. To simplify the design, processing, and testing of the experimental devices, not all circuit design rules were followed, such as the proper ground-signal-ground (GSG) wire coupling layout. Large wire dimensions and pads (about 3 mm) were used for ease of testing, with some signal loss as a result.
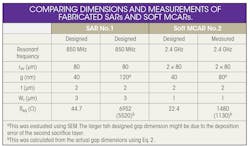
When the experimental devices were tested without DC bias, even for devices with only the wire layout (the first layer of the structure), a broad peak of S21 (the through signal) around 1 GHz was observed, indicating signal loss through radiation from wires. To eliminate the effects of radiation loss, the S21 signal value of the resonator ring was deducted from the signal value when it was at a bias of 0 V dc. When it was at a bias of 10 V dc, the resonant frequencies of the SAR and soft MCAR were observed (see table, Figs. 16-18).
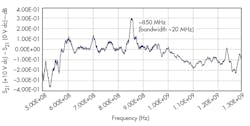
As demonstrated by the SEM of Fig. 12, the resonator width was 3 mm, corresponding to a resonant frequency of 850 MHz according to Eq. 1. Measurement results matched the simulated values. Figure 16 shows measurement results of a SAR resonator, which exhibited a resonant frequency of ~850 MHz. The peak signal at 850 MHz was only 0.3 dB above the background noise, indicating that RF circuit design and the MEMS process need to be improved.
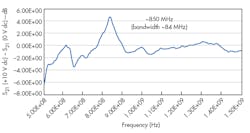
Measurement results for the soft MCAR also agreed with design simulations on the soft coupling ring. Figure 17 shows the measurement results for a soft MCAR with 3 mm ring width. Again, it demonstrated a resonant frequency of 850 MHz, but with a wider bandwidth of 84 MHz (10% of center passband frequency). The reason for the wider bandwidth was due to the insufficient vacuum environment of the resonator during measurement (>10 mTorr), as it is well known higher vacuum (<10-7 Torr) offers narrower bandwidth for resonators.2
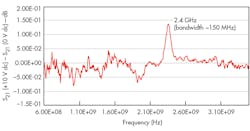
Measurements on a resonator with 1-mm width provide additional support for the MEMS filter design concept. The soft MCAR has a resonant frequency of 2.4 GHz with bandwidth of ~150 MHz (Fig. 18). The resonant frequency data also agrees with the calculation results from Eq. 1.
The bandwidth is larger than expected. However, this problem can be resolved by applying sufficiently high vacuum through a better experimental setup—e.g, using a turbopump instead of a mechanical pump alone. In real device applications, high vacuum for the resonator will be achieved by proper packaging and hermitically sealing, as widely used by mature technologies employed by shock sensor applications.
The impedance of a device under test (DUT) can be calculated using Eq. 9:
S11 = (Zin – Z0)/(Zin + Z0) (9)
where Zin equals 50 Ω (since measurements were normalized at 50 Ω) and Z0 was the impedance of a resonator under test.
RF signal loss was observed at bare wires and pads of fabricated devices. Thus, it was difficult to measure the impedance of the fabricated resonators directly. Instead, impedances of resonators before and after 10-V dc activation were calculated from the corresponding S21 VNA data. It was then assumed that the activated device was in parallel with the radiation part of the resonator when it was at 0 V dc. The calculated results indicated that the impedances were close to the values provided by Eq. 2, as shown in the table. An impedance of 1,480 Ω was reached—much lower than other MEMS concepts.
The measurement results demonstrated that the concepts were sound. The fabricated SARs and soft MCARs exhibited center bandpass frequencies at 850 MHz and 2.4 GHz, agreeing with design models. Soft MCAR filters showed wider bandwidth than SAR filters. Although the bandwidth is larger than expected, the issue can be resolved by improving the experimental setup to provide a better vacuum testing environment. The impedance results were also promising at <1.5 kW with an activation voltage of 10 V dc. The researchers are confident in being to achieve an impedance of 50 Ω by rigidly controlling the fabrication process.
Dr. Yin Liu, Senior Researcher
Dr. Zhi-fan Zhang, Researcher
LW Microsystems, Inc., 2 N. First St., Ste. 201, San Jose, CA 95113
References
1. A. Mohieldin, E. Sanchez-Sinencio, and J. Jilva-Martinez, “Design Considerations of Bandpass LC Filters for RF Applications,” Circuits and Systems, 2002, MWSCAS-2002: The 2002 45th Midwest Symposium.
2. J. Brank, et al., “RF MEMS-Based Tunable Filters,” International Journal of RF and Microwave CAE, Vol. 11, 2001, pp. 276-284, 2001.
3. C.T.-C. Nguyen, “Vibrating RF MEMS for next generation wireless applications,” Proceedings of the 2004 IEEE Custom Integrated Circuits Conference, Orlando, FL, October 3-6, 2004, pp. 257-264.
4. F. Bannon, III, J. Clark, and C. Nguyen, “High-Q HF Microelectromechanical Filters,” IEEE Journal of Solid-State Circuits, Vol. 35, No. 4, April 2000.
5. B. Bircumshaw, G. Liu, H. Takeuchi, T. King, R. Howe, O. O’Reillya, and A. Pisano, “The Radial, Bulk Annular Resonator: Towards a 50-Ω RF MEMS Filter,” Transducers ’03: The 12th International Conference on Solid State Sensors, Actuators and Microsystems, Boston, MA, June 8-12, 2003, pp. 875-878.
6. S. Li, Y. Lin, Y. Xie, Z. Ren, and C. Nguyen, “1.51-GHz polydiamond micromechanical disk resonator with impedance-mismatched isolating support,” Proceedings of the 17th International IEEE Micro Electro Mechanical Systems Conference, Maastricht, The Netherlands, January 25-29, 2004, pp. 821-824.
7. H.A.C. Tilmans, “Equivalent circuit representation of electromechanical transducers: I. Lumped-parameter systems,” Journal of Micromechanical and Microengineering, Vol. 6, 1996, pp. 157-176.
8. K. Wang, and C. Nguyen, “High-Order Medium Frequency Micromechanical Electronic Filters,” Journal of Microelectromechanical Systems, Vol. 8, No. 4, December 1999.
9. M. Demirci, M. Abdelmoneum, and C. Nguyen, “Mechanically corner-coupled square microresonator array for reduced series motional resistance,” Digest of Technical Papers, 12th International Conference on Solid-State Sensors & Actuators (Transducers’03), Boston, MA, June 8-12, 2003, pp. 955-958.
10. M. Madoc, Fundamentals of Microfabrication, CRC Press LLC., Cleveland, OH, 1997.
11. S. Timoshenko, Vibration Problems in Engineering, 4th ed. Wiley, New York, 1974
12. Y. Liu, “MCAR filters,” U.S. patent application in progress.
13. W. Young, et al., “Roark’s Formulas for Stress and Strain,” McGraw-Hill, New York, 2002, pp. 754-768.
14. A.I. Zverev, Handbook of Filter Synthesis. Wiley, New York, 1967.