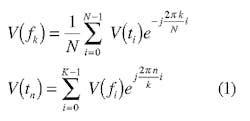Analyze Coax Cable Digital Pulse Distortion
This file type includes high resolution graphics and schematics when applicable.
Coaxial cables are often neglected during the characterization of high-speed digital components, even though such transmission lines can have a major electrical influence on a test setup. Coaxial cables are sometimes treated as lossy elements, and assigned a lumped capacitance and/or inductance, although the electrical effects of a coaxial cable can be much more complex than a single capacitance value.
What follows is an examination of how the electrical performance of a coaxial cable, notably loss and distributed capacitance/inductance, can affect the integrity of a high-speed digital pulse. The article will review the creation of a high-speed digital pulse, how to launch the pulse from an ideal output impedance, follow its transmission down an imperfect coaxial cable, and show how to make measurements at a perfect load.
To apply transmission-line theory to this analysis, the pulse will be created in the time domain and then converted to the frequency domain. To use the analysis tools available, the pulse is created as a discrete time pulse. The Fourier Transform, and inverse Fourier Transform for the pulse are1
where:
M = 17,
N = 2M,
K = 1 + 2M − 1
tn = Δt(− 2M − 1),
Δt = 0.25 ps,
n = 0...(N − 1)
fk = kf0,
f0 = 1/(2MΔt), and
k = 0...(K − 1). Note that the values for M and Δt have been chosen as required for optimal resolution and bandwidth.
At the input, this pulse is very narrow and has a finite rise time. It can be expressed mathematically as:
where:
A = amplitude,
π = the pulse width, and
tr = the 100-percent rise time, and
Transmission-line theory is well established and this analysis should be straightforward. Still, it may provide some reassurance by running a simple analysis that can be confirmed by means of time-domain-analysis techniques. In this case, a pulse will be launched from a nonideal source and transmitted a short distance to a nonideal load. The source and the load are connected by means of a short, lossless coaxial cable. The source is chosen to be 60 Ω, the cable is 50 Ω, and the load 40 Ω (Fig. 1).
These impedance mismatches will generate multiple reflections, which can be calculated using time-domain-to-frequency-domain-to-time-domain theory, and then verified using time-domain transmission-line theory.
The analysis will be presented as a time-domain graph of the source voltage, the input voltage, and the output voltage. The first step in the analysis is to convert the source voltage into the frequency domain by means of the Fourier Transform. In order to calculate the input voltage, the input impedance, which can be determined by the scattering parameter (S parameter) S11, is required. The S11 term can be calculated from the circuit's ABCD parameters2:
where:
βl = the electrical length of the cable .
From the ABCD parameters, S11 is3
The input impedance is:
The input voltage and current become:
The output voltage and current can be calculated using the ABCD parameters and the input voltage and current:
Page Title
Finally, the input and output voltages are transformed back into the time domain. Graphs of the source, input, and output voltages from this analysis are shown in Fig. 2.
The rise times (10 to 90 percent) of each signal are as follows: trs = 80 ps, trin = 80 ps, and trL = 80 ps at the output. The fact that all three rise times are the same is to be expected, since the source and load impedances are real and the cable connecting the source and load is without loss. But, although the cable is considered without loss, it nonetheless has distributed inductance and capacitance (see Fig. 3 and Eqs. 23 and 24).
In the frequency response of the source voltage, it should be noted that the finite rise time changes the frequency spectra from that of an ideal pulse. Because the coaxial cable is losses, the time-domain responses of the input and load voltages can be calculated using the reflection coefficients and the delay time of the coaxial line.
For a coaxial line with rise time of zero, the analysis is as follows. The reflection coefficients at the source and load, respectively, are:
At t = 0 seconds, a traveling wave of 2-V amplitude is incident on the input of the circuit. The voltage is immediately present at the input, and propagates toward the load. The input voltage, and the wave traveling toward the load (V+1), are:
The wave V+1 travels the length of the transmission line in 0.5 ns. At t = 0.5 ns, the traveling wave arrives at the load. Because of the impedance mismatch, a reflected voltage wave (V−2) is generated which propagates toward the input. The voltages at the load and the reflected wave are:
Wave V−2 travels to the input. Upon arriving at the input (t = 1 ns), another reflected wave is generated because of the impedance mismatch of the source.
At t = 1.5 ns, wave V+3 arrives at the load, and generates a reflected wave V−4. The reflected wave and load voltage are:
At t = 2 ns, wave V−4 arrives at the input. At the same time, a −2-V traveling wave from the source is incident on the input. The resulting wave, which travels toward the load, and the voltage at the input are:
SEE EQ. 18
SEE EQ. 19
SEE EQ. 20
At t = 2.5 ns, wave V+5 arrives at the load. The reflected wave and voltage at the load are:
Page Title
Reflections continue endlessly with decreasing amplitude, although no further reflections will be calculated for the sake of this analysis. Comparison with the time-to-frequency-to-time-domain technique shows the two techniques to be equal.
As this analysis shows, a coaxial cable can be approximated as a length of cable with characteristic impedance of 50 Ω terminated with two connectors of higher or lower characteristic impedance.4 Using this as a foundation, loss terms are added giving a reasonable model for a lossy cable with a nonzero reflection coefficient (VSWR). For the purpose of this analysis, the coaxial cable selected for study is designed for mode-free operation to 35 GHz.
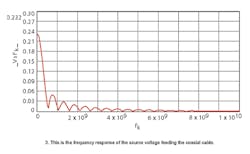
For formulating the S-parameters, the distributed circuit elements for each section of the cable will be calculated, combined into ABCD parameters, and finally converted to S-parameters to evaluate the VSWR and loss. The distributed element circuit model for this purpose is shown in Fig. 4.
The cable is broken into three sections, with characteristic impedances of 50 Ω for the cables and 54 Ω for the connectors. The cable, which is 36 in. long, has a dielectric constant of 2. The ratio of b/a in the cable is 3.25. The remaining parameters were chosen to produce the characteristic impedance and acceptable VSWR and loss curves. Omitted dimensions are ai, bi, and leni, and electrical parameters εr, tanδ, and σc2:
The exact characteristic impedance, and the propagation constant are:
The ABCD matrix for the cable is the combination of the ABCD parameters for the individual sections3:
The two S-parameters of interest are S11 and S21, calculated respectively in Eqs. 26 and 27:
As a quick check, the frequency spacing between peaks can be calculated as4:
which shows 17 peaks between grid lines, in agreement with measurements. The measured VSWR may differ with the calculated values, depending upon the number of measurement samples.
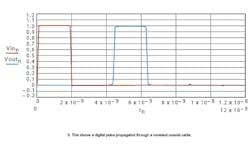
The primary interest in this analysis is the distortion effects of a coaxial cable on a digital pulse. When the pulse of Fig. 2 is applied to the experimental cable, the output of Fig. 5 results.
Although the source and load impedances are 50 Ω, because of the 54-Ω connectors there is some overshoot/undershoot and multiple reflections of the voltage Vin. In the case where the input is a pulse train, the multiple reflections would interfere with subsequent pulses. The exact interference would depend on the length of the cable.
While there is significant loss in the cable, the pulse is not reduced because of the pulse width. The 2-ns pulse is primarily contained in the first 500 MHz of bandwidth where the loss is lower. The rise times of the input and output pulses are given by:
while the propagation delay of the cable is given by:
Note that there was no change in rise time observed in the lossless cable (Fig. 2). When loss is added to the cable model, however, the rise time increases, demonstrating that increased rise time at the output of a cable is the result of cable losses.
It is tempting to take the formula for capacitance and inductance (Eq. 23) and multiple by the length of cable to obtain a total capacitance/inductance value and treat the cable as two lumped elements. For the cable described, the total capacitance and inductance are:
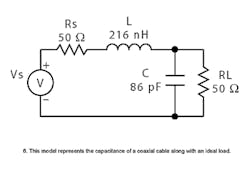
When the capacitance and inductance of the cable are treated as lumped elements and the loss and length ignored, the circuit becomes the one shown in Fig. 6.
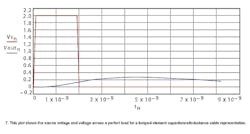
Applying the pulse of Fig. 2, the voltage from the source and that appearing across the load are described by Fig. 7.
Clearly, the cable cannot be treated as a lumped capacitance and inductance. Comparing Figs. 5 and 7, it is apparent that treating the cable as a lumped-element capacitance/inductance significantly alters the signal from that which would actually occur.
It is not a simple matter to calculate the losses for a pulse and the increase in rise time due to a coaxial cable. The pulse consists of many separate frequency components, each with a different loss value. As these components increase in frequency, so does the loss. Because the edges of a pulse are formed by higher-frequency components, there is an increase in rise time and a rounding of the pulse edges as a function of cable loss.
For the most accurate measurements when evaluating a digital pulse, it is recommended to first determine the frequency components of the pulse, and then determine the bandwidth in which the pulse is primarily contained. Provided that the cable loss at the high end of the pulse bandwidth is not too high, it can be assumed the coaxial cable will not significantly affect the pulse.
When the load appearing across the output of a circuit under test is of interest, it is possible to use the equations above to incorporate the parameters of a test cable as well as the input impedance of the test equipment. Mainly, the cable parameters are determined from Eqs. 23, 24, and 25. The impedance of the test equipment, and subsequent load impedance to the circuit, can be determined from Eqs. 4, 5, and 6.
REFERENCES
- R.E. Ziemer, W.H. Tranter, and D.R. Fannin, Signals and Systems, Continuous and Discrete, Macmillan, New York, 1983.
- D.M. Pozar, Microwave Engineering, Addison-Wesley, Boston, MA, 1990.
- I. Bahl and P. Bhartia, Microwave Solid-State Circuit Design, Wiley, New York, 1988.
- Bruce Bullard and E. Houghland, "Low VSWR Cables," Applied Microwave & Wireless, April 2001, pp. 110-114.
This file type includes high resolution graphics and schematics when applicable.